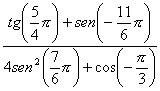b.
c.
disequazioni di II grado soluzioni
a.
b.
c.
d.
e.
f.
g.
h
i.
l.
di recupero
m.
1.
Dato il fascio di circonferenze
.
a. Determina l’asse radicale, gli eventuali punti base e il luogo dei centri.
b. Determina il valore di k per il quale la circonferenza ha il centro sull’asse delle y, scrivi l’equazione e disegnane il grafico. Determina la tangente alla circonferenza nel punto di intersezione con l’asse x (quello con ascissa minore)
c. Determina l’area del triangolo formato dalla tangente trovata, dall’asse radicale e dall’asse delle x.
2. disegna i grafici della funzioni
a.
b.
3.
risolvi la disequazione
4.
trasforma l’espressione in una che contenga solo cosa:
5.
sapendo che
con
determina il seno e la tangente.
6.
semplifica l’espressione:
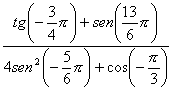
7.
Dato il fascio di circonferenze
.
a. Determina l’asse radicale, gli eventuali punti base e il luogo dei centri.
b. Determina il valore di k per il quale la circonferenza ha il centro sull’asse delle x, scrivi l’equazione e disegnane il grafico. Determina la tangente alla circonferenza nel punto di intersezione con l’asse y (quello con ordinata minore)
c. Determina l’area del triangolo formato dalla tangente trovata, dall’asse radicale e dall’asse delle y.
8. disegna i grafici della funzioni
a.
b.
9.
risolvi la disequazione
10.
trasforma l’espressione in una che contenga solo cosa:
11.
sapendo che
con
determina il seno e la tangente.
12.
semplifica l’espressione:
