La prova può far colmare il debito formativo in matematica e serve come valutazione iniziale per la classe.
1)
risolvi la seguente equazione di II grado:
ponendo
(spiega
perché?)
da cui
e quindi
(ho
usato la formula ridotta…problemi?) le
soluzioni sono quindi
entrambi accettabili (perché?)
2)
Nella seguente equazione parametrica
determina i valori di k
in modo che:
a.
Le due soluzioni siano coincidenti
da cui k = 1 e k = - 1/3 E’
chiaro come ho risolto l’equazione…scomposizioni, legge d’annullamento del
prodotto, delta quarti sono cose note per te?
b.
Le due soluzioni siano reali distinte
rifletti
sul simbolo “V” quando lo devo usare? E’ sbagliato dire “e” (cioàè
la V rovesciata) , perché?
c.
Le due soluzioni non siano reali
d.
Le due soluzioni siano opposte
Sei in grado di spiegare ogni passaggio? Se sì, sei
bravo, se no ha bisogno di rivederti alcune cose!!!
e.
Le due soluzioni siano reciproche
tutto chiaro?
f.
Una soluzione sia nulla k
= 1 subito! Perché?
g.
Spiega a parole come è possibile che il risultato del punto
d e f siano coincidenti con un risultato del punto a, qual è
l’equazione che ha questa caratteristica?
Ovviamente stiamo cercando una soluzione x = 0 (per il punto
f) coincidente con l’altra soluzione per il punto a, e sia opposta all’altra
e l’unico numero che soddisfa tutto è 0 (le due soluzioni 0 sono coincidenti
e opposte) . l’equazione è x^2=0 (si ottiene ovviamente sostituendo k = 1)
3)
Trova il perimetro del parallelogramma avente un vertice nel punto A(
4 , 1) e due lati sulle rette y = x + 6 e y =
- 3x – 2. Dobbiamo
a.
determinare le due rette
parallele alle date passanti per (4,1),
b.
determinare i punti di
incontro tra le rette trovate e le date
c.
determinare le distanze
da A dai punti trovati
e
il punto di intersezione tra la blu e la grigia è
e il punto di intersezione tra verde e rossa è
le distanze cercate sono
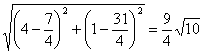e
da cui il perimetro
.
4)
In un triangolo rettangolo un cateto è lungo cm. 9 e la sua proiezione
sull’ipotenusa è 9/16 della proiezione
dell’altro cateto sull’ipotenusa. Trovare la misura del perimetro e
dell’area del triangolo.
La proiezione dell’altro cateto è x , la proiezione del
cateto dato è 9/16x per il I teo di Eu. si ha che x = 48/5 da cui l’ipotenusa
è 15 e l’altro cateto 12 (AREA 54 cm^2 e PERI cm.36)
5)
Determina il raggio del cerchio inscritto in un triangolo isoscele il cui
perimetro misura cm.36 e la base cm.10.
Chiamando x il
raggio si ottiene una proporzione del tipo 13:5=(12-x):x Bel
giochino capire perché! Da cui
il raggio è cm. 10/3 = cm. 3,(3)
6)
dimostra che in due triangoli simili le mediane relative a due lati
corrispondenti stanno tra loro come i due lati stessi
rapporto tra lati corrispondenti uguale implica rapporto tra
metà dei lati corrispondenti uguale, angoli uguali, rapporto tra altri due lati
consecutivi uguale per il primo
criterio di similitudine i triangoli formati da mediani, mezzi lati e altri lati
sono simili…forse se fai le figure capisci meglio!!!
Mandami
un’ Email per dirmi che sei
riuscito a leggere tutto o che hai trovato qualche errore (nessuno è
perfetto!!)