Prepariamo il compito del 21.10.02
1)
data la parabola
dette A e B le sue
intersezioni con l’asse x e V il vertice, determina
a.
per quali valori di k la retta
interseca la parabola
detto M il punto medio
delle intersezioni tra la parabola e la retta sopra quanto vale
facendo
il sistema tra parabola e retta e ponendo il delta maggiore o uguale a zero si
ottiene k<11, per k =11 si ottiene ovviamente la retta tangente
determiniamo le coordinate del punto M in funzione di k
sistema tra parabola e retta dà due punti di intersezione
quindi il punto medio M sta sulla
retta x = 4 con la y = -8+k
l’area MAB sarà data da (AB * MH)/2 con AB che vale 4
quindi
il vertice V è (3, 4)
quindi
ponendo il valore assoluto uguale a 8-k perché il limite ci interessa per k che tende a zero
quindi
2) in un triangolo isoscele ABC di base AB è inscritto un cerchio di raggio unitario. Indicato con T il punto di contatto tra le circonferenza con BC ponete AB=2x e CT=y ed esprimete y in funzione di x. Rappresentate la funzione così ottenuta (per qualsiasi x) indicando il tratto che ha senso per il problema.
Facendo la figura abbiamo la seguente proporzione
elevando al quadrato ed
esplicitando la y otteniamo
il cui grafico è quello in figura
(descrivi gli elementi dominio, intersezioni, segno, limiti, asintoti.) La parte che ha senso per il problema è per le x>1 perché per x compreso tra 0 e 1 otteniamo una y negativa (ci si dovrebbe però chiedere cosa è successo elevando al quadrato)
3)
esamina i punti di discontinuità per la seguente funzione
la funzione non è definita in x = 0 il limite per x che tende a 0 va a infinito la discontinuità è di II specie mentre non è definita per x = -3 ma il limite in questo caso tende a –1/27 quindi la discontinuità è eliminabile
4)
4) data la funzione
determinare per quale valore
del parametro a la funzione è
continua in
.Dopo aver determinato ogni altro
elemento necessario , rappresentare un grafico qualitativo della funzione
ottenuta.
Il limite per x che tende a 1- dà 1+a
Il limite per x che tende a 1+ dà 3 quindi 1+a=3 da cui a= 2
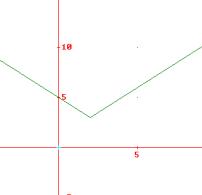
Il grafico è quello in figura.
5) risolvi i limiti
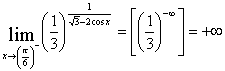
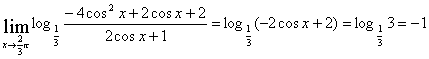
altri limiti potete trovarli sul testo.
6)
E’ data la funzione
, disegnane il grafico, determina se la funzione ha qualche simmetria e
verificalo attraverso le equazioni della simmetria.
La funzione è simmetrica rispetto all’asse x =2
Le equazioni della trasformazione sono
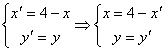e sostituendo si ha
che è ancora la stessa equazione.
FINE
