10 febbraio 2003 - compito di matematica - CLASSE 5 D

1)      studia la funzione ,

la funzione ha periodo 2p, si annulla dove si annulla il seno (e dove il coseno è 1, ma è lo stesso valore che annulla il seno)

max 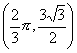 min flesso a tangente orizzontale (0,0) e (2p,0) (è in pratico sempre lo stesso che si ripete ogni 2p. altri flessi  x = p, x = arccos(1/4) x = 2p-arccos(1/4)

anche dal grafico ci rendiamo conto che la funzione è dispari (infatti y(-x)=-y(x) ma è simmetrica rispetto a qualsiasi punto (kp,0) con k intero  infatti se consideriamo un valore x, il valore simmetrico è x’ = 2kp-x  sostituendo otteniamo y(2kp-x)=y(-x)= -y(x)

2)      fra tutti i triangoli isosceli inscritti in un cerchio di raggio di misura r, qual è quello che ruotando intorno alla sua base genera il solido di volume massimo? Indica se per la funzione volume che ottieni, nell’intervallo dove studi l’incognita scelta ha significato, può essere utilizzato il teorema di Rolle e se sì cosa può essere desunto.

facendo ruotare si ottengono due coni (uguali) con la base in comune. indicando con x il raggio della base comune (altezza del triangolo isoscele) si ottiene che le altezze misurano

poiché i due volumi misurano , l’incognita scelta varia tra 0 e 2r, sugli estremi il valore del volume è 0 (un punto nel caso x = 0 e una doppia base nel caso x = 2r). quindi essendo la funzione continua e derivabile, assumendo valore uguale sugli estremi, vale il teorema di Rolle che mi garantisce l’esistenza di un punto interno dove la derivata si annulla (in questo caso sarà un massimo perché valendo sugli estremi zero, il volume è costretto a ‘crescere’ comunque

la derivata si annulla internamente per x = 5/3r, il punto è un massimo come è confermato dal segno di 5r-3x.

3)      Uno studente esegue tre problemi su argomenti diversi. La probabilità di svolgere correttamente il primo problema è 0,5. La probabilità di svolgere correttamente il secondo è 0,25 e la probabilità di svolgere correttamente il terzo è 0,8.

a.       determina la densità (distribuzione) di probabilità della variabile aleatoria X che conta il numero di problemi corretti.

b.      qual è la probabilità di fare corretti almeno due problemi?

c.       qual è la probabilità di fare corretti al massimo (al più) un problema?

d.      se la valutazione per ogni problema corretto è 2,5 punti, qual è il voto sperato?

X                     0                                  1                                  2                                  3

p                      0,075                           0,4                              0,425                          0,1

la probabilità di fare almeno due problemi è P( X= 2) + P( X =3) = 0,525

la probabilità di fare al più un problema è P( X =0)+ P( X =1) = 0,475

il voto sperato è E[ X]= 1,55 che moltiplicato per 2,5 fornisce 3,875 (forse 4 se il prof è buono)

4)      risolvi i seguenti limiti:

1)                  

2)                       

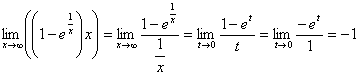
 3)

orientiamoci al compito di esame: a scelta risolvi uno dei seguenti quesiti:

a)      nella funzione  determina i punti di non derivabilità, fornendo esaurienti motivazioni.

x = 3 è punto di non derivabilità perché è di non continuità, x =2 è un probabile punto di non derivabilità. Per verificarlo è bene spezzare la funzione

la derivata allora sarà limite sinistro è -2 e il limite  destro – 4 confermando la non derivabilità in x = 2.

b)      determina una approssimazione, con un errore < 1/100 (cioè la differenza tra la soluzione esatta e la soluzione approssimata deve essere minore di un centesimo) dell’equazione

osserviamo prima graficamente quando logx  = -x

osserviamo un punto di incontro per 0<x<1

infatti il teorema di esistenza degli zeri applicato all’intervallo 0,1;1 offre

y(0,1)= numero che tende a – infinito + 0,1 quindi negativo

y(1)= 1

provo

y(0,5)=log(0,5)+0,5=-1.9

y(0,75)=log(0,75)+0,75=0,4

quindi la soluzione è 0.5<x<0,75

y(0,63)=0,16

quindi la soluzione è 0,5<x<0,63

y(0,56)=-0,02

quindi la soluzione è 0,56<x<0,63

y(0,60)=0,08…

quindi la soluzione è 0,56<x<0,60

y(0,58)=0,03 quindi la soluzione è 0,56<x<0,58

y(0,57)=0,007 quindi la soluzione è 0,56<x<0,57

y(0,565)=-0,006 quindi la soluzione è 0,560<x<0565 risulta chiaro che la soluzione poiché l’ampiezza dell’intervallo è 5/1000 l’approssimazione è <1/100 come richiesto (l’approssimazione corretta è 0,57. (la soluzione calcolata con derive con 6 cifre decimali è 0,567143)

c)      da cosa è rappresentato l’insieme di soluzioni dell’equazione

ü      dal punto (3, -4)

ü      non ci sono soluzioni

ü      dall’unione delle due rette

ü      dai punti appartenenti all’iperbole

            scegli la risposta corretta, motivando la scelta.

la risposta corretta è l’unione delle rette x = 3 e  y = -4 in quanto la scrittura può essere scomposta come segue per la legge di annullamento del prodotto tutti i punti che rendono x-3=0 e/o tutti i punti che rendono y+4=0 verificano l’equazione: sono i punti che stanno sulle due rette!

 fine compito