1)
E’ data la conica di equazione
![]() ,
,
a.
dopo aver considerato di che si tratta di un’ellisse e aver detto perché,
determina le equazioni di una rotazione che porti la conica ad avere l’asse
focale coincidente con l’asse y.
b.
Verifica che il triangolo
che ha per base l’asse minore e il terzo vertice sull’ellisse, ha l’area
in funzione di x rappresentata da una delle due semiellissi e determina
allora il valore massimo di questa area.
c.
Determina poi la trasformazione che trasforma l’ellisse in una
circonferenza
d. Trova l’immagine del triangolo di area massima trovato prima e trovane l’area.

la trasformazione è
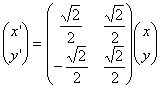
cioè una rotazione di 45° in senso orario (ovvero di –45°)
e otteniamo una ellisse di
equazione
![]()
il triangolo ha base 2,
l’altezza
![]() quindi
quindi
![]() che corrisponde alla semiellisse superiore quindi deduciamo che l’area è
massima quando è massimo il valore della y, ovvero quando x è 0.
che corrisponde alla semiellisse superiore quindi deduciamo che l’area è
massima quando è massimo il valore della y, ovvero quando x è 0.
la dilatazione è
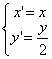 e la circonferenza che otteniamo è
e la circonferenza che otteniamo è
![]() , poiché il determinante è ½ , l’area dell’immagine del triangolo di area
massima è 1.
, poiché il determinante è ½ , l’area dell’immagine del triangolo di area
massima è 1.
2)
risolvi la disequazione
![]()
![]()
![]()
![]()

3)
dati i punti A( 1 , 0 ) e B(-
2 , 3 ).
a.
Scrivi in forma parametrica la retta passante per A e B.

![]()
b.
Trovato il vettore direzione determina un vettore ad esso perpendicolare
e la retta passante per A che
per direzione ha il vettore trovato. (in forma parametrica)
un vettore può essere
![]() quindi la retta
quindi la retta
![]()
c.
Considera il parallelogramma che ha due lati lungo le direzione dei due
vettori determinati al punto b (con O vertice del parallelogramma). Determina,
a partire dai vettori che hai usato come direzione, per quali scalari devi
moltiplicare ogni vettore affinché il quadrilatero abbia area 10, il problema
ha una soluzione unica? e se vogliamo che il quadrilatero sia un quadrato (se
possibile)?
dobbiamo determinare i moduli dei
vettori scelti: in entrambi sono
![]()
quindi
![]() quindi la soluzione non è unica, ma se vogliamo che il quadrilatero che è
sicuramente un rettangolo sia un quadrato i due lati saranno uguali quindi
quindi la soluzione non è unica, ma se vogliamo che il quadrilatero che è
sicuramente un rettangolo sia un quadrato i due lati saranno uguali quindi
![]()
4)
risolvi le equazione e le disequazioni esponenziali:
![]()
![]()
 oppure
oppure
![]()

![]()
![]()
![]()
le
ultime due disequazioni non hanno soluzioni perché le funzioni esponenziali
sono sempre positive
5)
a.
risolvi le equazione logaritmiche
![]()
![]() purché x > 0 quindi x=2
purché x > 0 quindi x=2
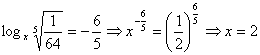
b.
trasfoma l’espressione (expand)
![]()
trasforma l’espressione (collect)
 purché
purché
![]()