COMPITO DI MATEMATICA
CLASSE 4D – 14 dicembre ’02
ricorda, alla fine della lettura, chiediti:
sono in grado di rifare il compito... (ci puoi anche provare!)
ho capito dove ho fatto errori e perchè
cosa mi propongo per migliorare il raggiungimento degli obiettivi non raggiunti
Se
hai problemi scrivi
Data
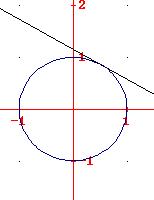
una circonferenza di raggio unitario e una sua corda
![]() a distanza metà del raggio dal
centro O, determina un triangolo AMB con vertice M sul
maggiore dei due archi AB. Dopo aver trovato l’angolo M e aver
verificato, motivandolo, che questo angolo è fisso.
a distanza metà del raggio dal
centro O, determina un triangolo AMB con vertice M sul
maggiore dei due archi AB. Dopo aver trovato l’angolo M e aver
verificato, motivandolo, che questo angolo è fisso.
Dal
momento che la distanza di AB da 0 è ½ otteniamo che
![]() e come abbiamo già visto (o applicando il teorema della corda in modo inverso
l’angolo corrispondente sull’arco maggiore (angolo in M) misura 60°(cioè
p/3). Indicando con x uno dei due angoli alla base otteniamo _
e come abbiamo già visto (o applicando il teorema della corda in modo inverso
l’angolo corrispondente sull’arco maggiore (angolo in M) misura 60°(cioè
p/3). Indicando con x uno dei due angoli alla base otteniamo _
![]() oppure scambiati ma la funzione rimane sempre la stessa:
oppure scambiati ma la funzione rimane sempre la stessa:

Le
situazioni limite saranno x = 0 e
x= 2p/3 in entrambi i casi la funzione vale rad(3) ovvero la lunghezza della
corda, come può essere verificato anche dalla rappresentazione analitica.
Nel
grafico abbiamo le seguenti funzioni disegnate
![]()

Quindi
un modo di risolvere l’equazione equivale alla ricerca dei valori per cui la
funzione è 2rad(3) e la risposta è ovvia (anche dal grafico)…pi/3+2kp in
modo che il seno sia 1.Oppure utilizziamo

 da
cui come unica soluzione vediamo ancora pi/3+2kp
da
cui come unica soluzione vediamo ancora pi/3+2kp
Considera
la trasformazione lineare
![]() . scrivi la trasformazione in forma
matriciale (tale forma deve essere del tipo
. scrivi la trasformazione in forma
matriciale (tale forma deve essere del tipo
![]() )
)
Dalle
proprietà della matrice desumi, dallo studio dei punti uniti e delle rette
unite desumi di che trasformazione si tratta. Verifica trasformando il triangolo
di coordinate (1,0) (3,0) (1,1).
In
forma matriciale
![]() dalla matrice osserviamo che si
tratta di una rotazione (similitudine diretta con determinante 1). Con la
ricerca del punto unito che è (1,0) determiniamo il centro di rotazione, dalla
matrice e dalla rotazione desumiamo che la rotazione è di +90° .
dalla matrice osserviamo che si
tratta di una rotazione (similitudine diretta con determinante 1). Con la
ricerca del punto unito che è (1,0) determiniamo il centro di rotazione, dalla
matrice e dalla rotazione desumiamo che la rotazione è di +90° .
Inverti
la trasformazione usando il calcolo matriciale (o in altro modo ma il punteggio
sarà minore) verificando attraverso con lo stesso triangolo la correttezza
dell’inversione e osservando ciò che ritieni opportuno sulla matrice
ottenuta.
La
trasformazione inversa, partendo dalla matrice inversa, sarà
![]()
Calcolare
x e y in modo che risulti
a)
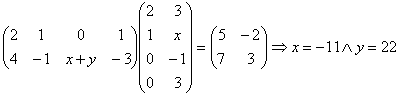 b) data
b) data
![]() calcola
calcola
![]() .
.
per
quali valori è vera l’uguaglianza
 da cui
da cui
![]() (b-a)=0 da cui a=1 b=1 a=b
(b-a)=0 da cui a=1 b=1 a=b
per quali valori di x è vera la disuguaglianza
![]() via alternativa
via alternativa
![]()
inverti
la matrice
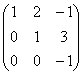 e verifica che il prodotto con la matrice di partenza dà l’identità. La
matrice inversa è
e verifica che il prodotto con la matrice di partenza dà l’identità. La
matrice inversa è
 .
.