COMPITO DI MATEMATICA
CLASSE 4D – 14 novembre ’02
1)
LE EQUAZIONI
i.
ii.
si trasforma in
da cui
iii.
da cui
soluzioni:
iv.
chiamando
abbiamo l’equazione
da cui
2)
LE DISEQUAZIONI
i.
da cui
ii.
risulta
3)
IL PROBLEMA
Un
quadrilatero ABCD ha i tre
angoli
,
e
di uguale ampiezza. Calcola le
funzioni trigonometriche (seno, coseno e tangente) dell’angolo
, sapendo che
. A priori cerca di costruire, basandoti su una costruzione grafica degli
angoli, il quadrilatero. A posteriori controlla se il quadrilatero costruito
rispetta i risultati trovati, facendo le dovute osservazioni sulla costruzione e
i commenti necessari.
in giallo è rappresentata
l’ampiezza dei tre angoli uguali.
Per determinare l’ampiezza
dell’angolo D, indicando con alfa l’angolo A, otteniamo
da cui
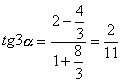quindi
a questo punto
ne deduciamo che
il segno “meno” è giustificato
dal fatto che essendo gli angoli uguali tutti e tre minori di 90° , il quarto
angolo è > 90° quindi il coseno è negativo.
quindi
il disegno può essere
4) LE TRASFORMAZIONI
E’ data una
trasformazione lineare (l’origine O è unita) che manda il punto
in
e il punto
in
.
a. Determina le equazioni della trasformazione e in base alle proprietà della matrice classifica la trasformazione.
La trasformazione cercata ha equazione
ottenuta
tramite la soluzione di semplici sistemi. La trasformazione è una rotazione in
senso antiorario di 60°.
b.
Mediante la trasformazione trovata, determina l’immagine della conica
e in base al risultato, disegna la
conica di partenza.
Invertendo la trasformazione si
ottiene
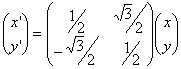e
sostituendo abbiamo e semplificando, otteniamo
c.
Analizza la trasformazione di equazione
, come sopra, deducendo in base alla matrice di quale trasformazione si tratta (
puoi avere informazioni utili trovando i punti uniti…); inverti la
trasformazione. Cosa ottieni? Come motivi il risultato ottenuto?
La
trasformazione ha la forma di una similitudine, ha determinante –1 quindi è
indiretta ed equivalente quindi è una simmetria assiale. Se ricerchiamo i punti
uniti otteniamo la retta
, che è il nostro asse di simmetria. Invertendo la trasformazione otteniamo
ancora la stessa trasformazione che è confermato dall’essere simmetria
assiale per tornare al punto di partenza si applica due volte la stessa
simmetria.
d. Trasforma ancora la conica al punto b. mediante la trasformazione al punto c. Cosa puoi osservare? Hai un contributo significativo per disegnare bene il grafico della conica? Perché? Commenti.
Trasformando la conica si ottiene ancora la stessa conica e questo sta a significare che l’asse di simmetria della trasformazione è anche asse della parabola. E’ ovvio che la parabola la posso disegnare partendo dalla y=x^2 e ruotandola di 60° in senso orario, ma conoscendo l’asse (inclinato di 30° rispetto all’asse x) posso fare il disegno più preciso.