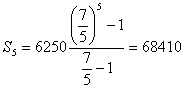compito di matematica 4d

3 aprile 2003

1)     E’ data la funzione  . Determina il grafico della funzione f(x)  (campo di esistenza, intersezioni con gli assi, segno, comportamenti agli estremi del campo di esistenza, massimi e minimi relativi con il metodo delle rette di livello: sistema con y = k). disegna poi il grafico del valore assoluto di f(x) ed infine .

note: disegna i tre grafici in colonna, facendo attenzione a gestire gli errori controllabili: in una funzione basta sostituire il valore di x per saper se il valore di y è quello previsto.

1)       in nero la f(x)

2)       in rosso il valore assoluto

3)       in verde il logaritmo

nella funzione valori importanti

passa per i punti

(0,0) e (1,0)

x = 2 e x = -2

sono asintoti verticali

y = -1 

è asintoto orizzontale e incontra l’asintoto nel punto x = 4.

il minimo è

 il massimo

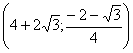
 nel logaritmo i punti di intersezione con l’asse delle x sono

2)  risolvi la disequazione

il numeratore è sempre negativo escluso per dove vale 0. Il denominatore è negativo per

–1<tgx<-1 ovvero - che è quindi la nostra soluzione

tre) risolvi le disequazioni

a.     

infatti il grafico di è quello rappresentato

la parte in verde rappresenta la parte di logaritmo che risolve la disequazione

b. 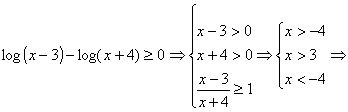     Æ

quattro) dimostra per induzione che vale per ogni n la seguente somma

per n =0 la somma vale 2 e la scrittura 1*4/2=2           vale per n=2

suppongo vero per n

dimostro per n+1:

 CVD.

cinque) Determina la lunghezza dei cateti di un triangolo rettangolo sapendo che sono in progressione aritmetica con l’ipotenusa e che quest’ultima misura 10cm. Verifica, attraverso la formula,  che il perimetro è la somma della progressione.

x, x + d, x + 2d sono i cateti e l’ipotenusa: sapendo che  

quindi poiché x + 2d = 10 abbiamo d = 2 cm. quindi

            primo cateto x = 3d = 6cm

            secondo catedo x + d = 3d + d = 8 cm

            ipotenusa  x + 2d = 3d + 2d = 10 cm

 cvd.

sei) una popolazione di topi è composta da 6250 individui. Ogni anno, per ogni 100 individui ne nascono 100 e ne muoiono 60. Determinare la consistenza della popolazione dopo uno, due, tre, quattro e cinque anni. Verificare che i numeri costituiscono una progressione geometrica, determina la ragione, verifica attraverso la formula, la somma.

su 100 abbiamo + 100 – 60 quindi 140 topi in più quindi per 6250 saranno

6250/100*140       =   8750      dopo un anno

8750/100*140       = 12250      dopo due anni

         = 17150      dopo tre anni

         = 24010      dopo quattro anni

somma                  = 68410

 chiaramente la ragione è 140/100 ovvero 7/5. La  formula infatti dà