3d 27 febbraio 03

1)     E’ dato il fascio di parabole .

a.      Determina gli eventuali punti base

b.      il luogo dei vertici

c.      la parabola passante per l’origine

d.      la parabola con vertice sull’asse delle y

e.      il fascio di circonferenze che ha per punti base i vertici delle due parabole trovate ai punti c. e d.

f.       tra le circonferenze del fascio determina quella passante per l’origine

1. ha un solo punto base (1,-3)  (le due generatrici sono la retta  y = -4x + 1 e la retta x = 1)
2. il luogo dei vertici è la retta y = -2x –1
3. la parabola passante per l’origine è per k=-1    V(-1,1)
4. la parabola con vertice sull’asse y è per k = -2   V(0,-1)
5. usando la retta passante per i due vertici 2x+y+1=0 e la retta avente come estremi del diametro  i due vertici  si ha come fascio

 scritta in altro modo  che passa per l’origine per k = 4

f. ovvero è la circonferenza

2)     In una semicirconferenza di raggio unitario inscrivi un rettangolo che abbia la base sul diametro. Per quali valori dell’altezza, la diagonale del rettangolo è maggiore della differenza tra il triplo della altezza con il raggio?

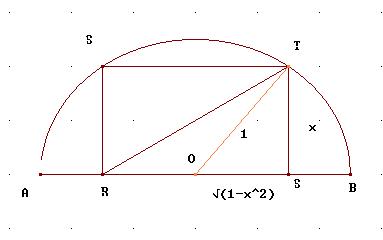
la condizione è  TR > 3TS – 1

con TS = x  con

 per x =0 il rettangolo diventa il diametro e la diagonale coincide con il diametro (2> - 1 e verifica la disequazione) con x = 1

il rettangolo coincide con il raggio e anche la diagonale coincide  (1>2 e non verifica)

 da cui  

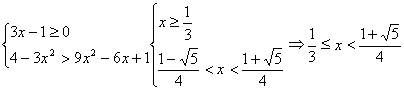
le soluzioni della disequazione sono mentre le soluzioni del problema sono per le limitazioni della x nel problema.

Una persona ferma sulla riva di in canale vede un albero sulla riva opposta sotto l’angolo di 58°15’ (l’angolo cioè tra la retta orizzontale e la retta passante per la cima dell’albero con origine nella persona), allontanandosi di 50m dalla riva del mare lo sotto un angolo di 26°15’. Calcola l’altezza dell’albero e la larghezza del canale. Ti consiglio di risolvere il problema prima letteralmente e sostituire i valori alla fine.

a = 58°,25

b= 28°,25

(ovviamente 15’ = 0,25°)

R = 50m.

da determinare H e L

poiché

e

3)    

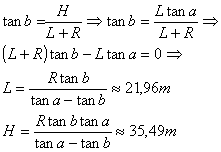
4)     Semplifica l’espressione:

a.     

b.     

c.      dato  sapendo  determina il coseno e la tangente dell’angolo 

d.      dato  sapendo che  determina il seno e il coseno dell’angolo.

 il seno è stato scelto negativo.

 il coseno è stato scelto negativo.

eliminato dal compito

5)     è data l’espressione  determina i valori di t per i quali l’espressione ha senso e per quali valori di t il seno è positivo quindi  0<a <p  .la condizione è

questo è vero quando  se vogliamo che il seno sia positivo avremo  quindi è t < - 2. 

  In generale determina il coseno e la tangente considerando p/2<a <p. (la soluzione di questo problema rende facoltativa, anche se consigliata, la soluzione del problema 4.c)

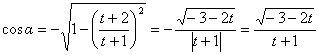 il valore del coseno deve essere negativo mentre t+1 sicuramente negativo.

 dato dal rapporto tra  seno e coseno negativo.

con t = -3 otteniamo

 fine compito torna Home