23 gennaio ’03

compito di matematica CLASSE 3 D

1)      Determina l’equazione della circonferenza passante per e e il cui centro appartiene alla retta . Conduci per le tangenti r e s alla circonferenza e la tangente t per A.

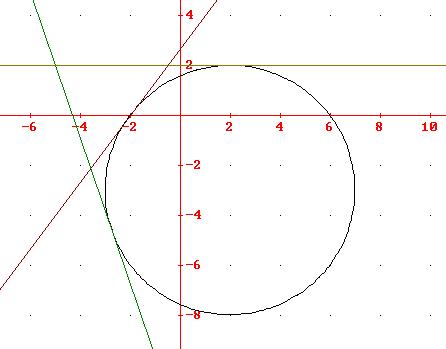
La circonferenza cercata ha un asse x = 2 che intersecato con la retta del centro dà y = -3, il raggio vale 5 quindi l’equazione è  le tangenti r e s si trovano mediante la formula della distanza tra fascio di rette e centro. Il fascio ha equazione  quindi 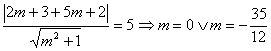le rette sono quindi  la retta t viene trovata cercando il coefficiente angolare del raggio nel punto di tangenza che è –3/4 quindi la retta è

 2)      Scrivi l’equazione della parabola con asse parallelo all’asse y sapendo che passa per e che la tangente nel suo punto è parallela alla bisettrice del 1° e 3° quadrante. Determina i punti della parabola che formano un triangolo di area  con il segmento staccato dalla parabola sull’asse x e determina l’area del poligono formato dai punti così ottenuti.

la retta che ci interessa è la retta x – y + 1 = 0 quindi la parabola tangente alla retta passante per il punto C è sostituendo le coordinate di A si ha . Da cui la parabola è . Poiché il segmento staccato sull’asse delle x misura 3/2 essendo il secondo punto di intersezione il punto B(1,0) deduciamo che l’altezza del triangolo (considerando il segmento come base) sarà 1 allora i punti che rispondono alla richiesta sono quelli che hanno ordinata 1 o –1  che si ottengono risolvendo le relative equazioni. o ; quindi abbiamo quattro punti i quattro punti formano un trapezio la cui altezza misura 2, la base minore ½ , la base maggiore quindi l’area misura

3)      Disequazioni

                                                               i.      la soluzione porta a da cui essendo la prima delle due disequazioni sempre falsa.

                                                             ii.      la scomposizione in fattori porta a e quindi

                                                            iii.     

la soluzione è

4)      risoluzione grafica di disequazioni

                                                               i.     

arco di parabola con retta

 la retta sta sotto la parabola tra 1 e 2 (prima di 1 non c’è niente, dopo 2 la retta sta sopra la parabola quindi le soluzioni sono

nota che  x = 1 è compreso infatti la parabola vale 0 mentre la retta vale –1, x = 2 invece no: la parabola vale 1 come la retta quindi sono uguali

                                                             ii.     

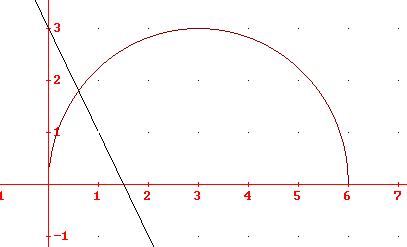
arco di circonferenza e retta. la circonferenza sta sotto la retta quando la x sta tra 0 e 3/5 (il valore è ottenuto intersecando la circonferenza con la retta). quindi il risultato è

 anche in questo caso nota che x = 0 è compreso: la circonferenza vale 0 mentre la retta vale 3. mentre x = 3/5 no perché circonferenza e retta sono uguali.

torna all'indice