5 dicembre ’02

compito di matematica CLASSE 3 D

  torna indietro alle pagine di presentazione

1)      Determina le equazione delle due circonferenze che hanno il centro sulla retta  e sono tangenti alle rette  e . (questa parte risolta correttamente rende il problema sufficiente) In base all’osservazione del grafico, nota che una delle due tangenti lascia le due circonferenze dalla stessa parte (appartengono allo stesso semipiano generato dalla retta tangente). Determina l’equazione dell’altra tangente alle due circonferenze, che lascia le due circonferenze dalla stessa parte. Determina il punto di incontro tra le due tangenti prese in considerazione e l’area del triangolo formato da detto punto di incontro e dai due punti di tangenza tra le due tangenti (una delle due di partenza e la terza tangente trovata) e la circonferenza di raggio maggiore.

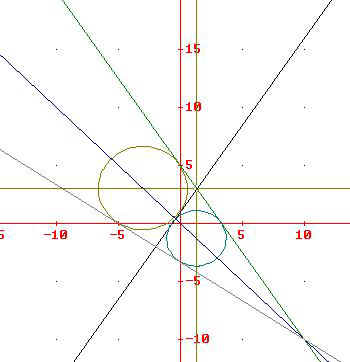la prima retta è x+y=0 è la bisettrice al secondo e quarto quadrante. Le altre due rette scritte in forma esplicita sono  e  (passano per (0,5) e per (0,1) e hanno un’inclinazione del tipo ‘se x cresce di 2, y decresce o cresce di 3).

I centri delle circonferenze stanno ovviamente sulle bisettrici degli angoli formati tra le due rette:  che forniscono come risultato y = 3 e  ; dalle intersezione otteniamo che il primo centro è (-3,3) mentre il secondo è ; per determinare i raggi calcoliamo la distanza dai centri a una delle rette (scelgo la seconda perché ha i numeri più piccoli)

  e 

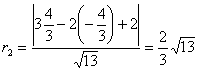
da cui le circonferenze hanno equazione

         e         

la tangente che ha la proprietà richiesta è la prima delle due (coefficiente negativo). Si verifica facilmente che anche la prima circonferenza passa per (0,5) oppure attraverso un sistema; può essere verificato che la seconda circonferenza è tangente in . L’altra tangente cercata è simmetrica rispetto alla prima rispetto alla retta x + y = 0 essendo le due circonferenze simmetriche rispetto a tale retta: la tangente cercata passerà per i punti (-5, 0) e La retta passante per quei punti è

complementi 1

la retta in questo caso è stata trovato osservando la simmetria di due punti e ricostruita come retta passante per i due punti, ma possiamo anche usare le simmetrie. La simmetria rispetto alla retta considerata è  si scambiano le coordinate e cambiano di segno; invertendo la trasformazione abbiamo  e sostituendo nella retta di  cui vogliamo trovare la simmetrica otteniamo  che è l’equazione che abbiamo trovato.

Il punto di intersezione è (10;-10).  La base del triangolo misura  e l’altezza 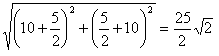  da cui l’area in questione vale

                           i.      Sono date due circonferenze: la prima L di equazione   e la seconda M di equazione . Disegna i grafici, determinando centri e raggi, determina la tangente comune alle due circonferenze e la retta c sulla quale giacciono i centri. Sulla retta dei centri determina il punto P intersezione della retta c con la circonferenza L, ma che non appartiene a M; determina l’equazione della circonferenza N che ha per diametro il centro di M e il punto P.(questa parte risolta correttamente rende il problema sufficiente). Determina le intersezione T e S tra le due circonferenze M e N e le rette PT e PS. Osserva le rette. Quale caratteristica hanno? Motiva la risposta. Avresti potuto trovare le rette passanti per P, con quelle caratteristiche, operando in altro modo? Quale? Fallo se hai tempo. 

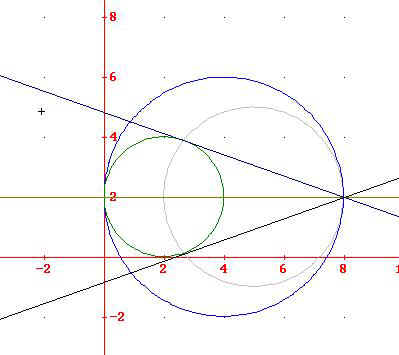le due circonferenze

M centro in (4,2) e raggio 4

N centro in (2,2) e raggio 2.

La tangente comune è la retta x = 0

La retta dei centri è la retta y = 2

Il punto (8,2) è il punto cercato.

La circonferenza N che ha per diametro il punto (8,2) e il centro (2,2) e quindi raggio 3 ed equazione  

Intersechiamo questa circonferenza con la circonferenza piccola otteniamo i due punti.

 (che è anche l’asse radicale tra M e N) e

le rette che passano per i punti 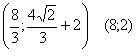 e 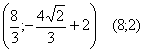 che sono le rette di equazione  sono le rette tangenti da P a M perché l’angolo che il raggio nel punto di incontro della retta e la retta è un angolo retto in quanto l’angolo è sotteso a una corda che è il diametro

Complementi 2: il metodo ‘classico’ per trovare le tangenti è il seguente

Prendiamo il fascio di rette passanti per (8,2) avrà equazione  imponiamo che le rette del fascio abbiano distanza dal centro di M  ovvero da (2,2)  pari al raggio che è 2 ovvero 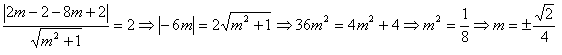che sostituiti nell’equazione del fascio danno ancora le rette trovate precedentemente.

                         ii.       

a. 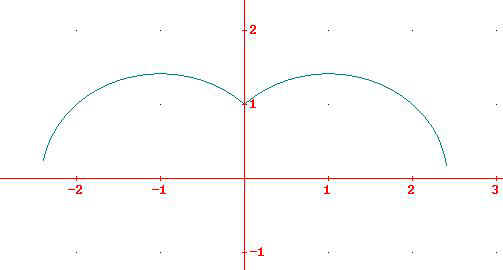      disegna il grafico di

l’equazione può essere riscritta nel seguente modo: 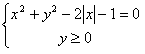 . l’equazione, a seconda del valore assoluto assume le due forme seguenti 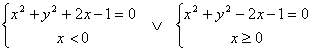 la prima è una (semi)circonferenza di centro (-1,0) e raggio , la seconda di centro (1,0).

.il grafico non è ottimale: le due semicirconferenze arrivano a toccare i punti .

b.      risolvi graficamente la disequazione .

Trasformiamo la disequazione in 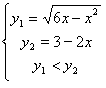  la prima equazione è una semicirconferenza di centro (3.0) e raggio 3. la seconda è una retta, la zona che verifica la richiesta è l’intervallo

4)

a.       data la disequazione  . Determina le soluzioni (i valori di x) al variare di a.

ovviamente perché l’equazione associata abbia soluzioni a deve essere maggiore di 0 e le soluzioni saranno  in questo caso la disequazione è verificata per valori interni all’intervallo tra le due soluzioni. Se a =0 si ottiene –4<0 sempre vero. Se a<0 l’equazione associata non ha soluzioni (delta <0) e poiché a<0 il polinomio è sempre negativo quindi la disequazione sempre vera. Schematizzando

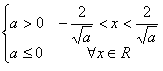
b.      al variare di x determina il segno del quoziente  

facendo il dovuto ‘cimiterino’ otteniamo

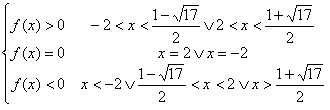 ovviamente il quoziente non esiste per

e risolvi le disequazioni  : la prima disequazione è il primo rigo di risultati, la seconda è l’unione della prima riga con la seconda (ovvero a –2 e a 2 ci sono anche gli uguali), la terza è l’unione della seconda con la terza.

Siamo arrivati in fondo: al solito se hai domande commenti o sfoghi SCRIVI e ricordati dopo la lettura di tornare a vedere cosa c’è scritto in cima: le cose nuove che devi ricavare dalla soluzione del compito e quelle vecchie che ti erano sfuggite…