CLASSE 5d

Verifica del debito formativo – Valutazione della situazione della classe

23 settembre ’02

1)     Studiare la funzione  determinandone il grafico

antidoto orizzontale y = 0 asintoti verticali x = -2 e x = 2, intersezioni con assi (1,0) e (0, ¼)

2)     Risolvi le seguenti disequazioni

a.     

il denominatore può essere ricondotto ad essere >0 se   , quindi considerando anche il segno del denominatore otteniamo

b.    

 l’equazione diventa considerando che vale solo quando x>1 posso dividere per x e ottenere il risultato è quindi 1<x<2

c.       la disequazione diventa il sistema

3)      

a.      E’ data la seguente definizione ; scrivi in simboli adeguati il limite e descrivi le possibili situazioni relative a questo limite.

 possibili grafici   

b.     Dal grafico scrivi correttamente il limite, usando i valori (x = 2…) indicati nel grafico e scrivi la definizione del limite scritto (sia usando i numeri, sia la definizione generica)

   che corrisponde alla definizione generica:

 relativa a

c.      E’ dato il seguente limite , dà la rappresentazione grafica e scrivi la definizione relativa.

 )     Discuti il seguente sistema  determinando le soluzioni.

Il sistema è determinato per con soluzioni

Il sistema per h = 0 diventa impossibile

Il sistema per h = 4 è indeterminato  con soluzioni (ad esempio):

5)     E’ data la parabola  che mediante una trasformazione diventa la parabola  ; determina le equazioni della trasformazione (che deriverà dalla composizione di due trasformazioni più semplici) e determina, se ci sono, elementi uniti (riflettendo sulla natura delle trasformazioni ed eseguendo i calcoli relativi)

Una possibilità evidente è la seguente

1)     una dilatazione che trasforma la parabola nella parabola

2)     una traslazione che “sposti” la parabola verso l’alto.

  da cui la trasformazione finale, ricambiando gli indici  per verificare sostituire 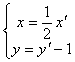nell’equazione della parabola di partenza: 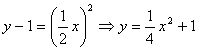 C.V.D.