sappiamo che

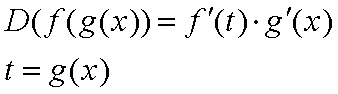
che significa che facciamo la derivata come  se g(x) fosse una variabile indipendente e moltiplichiamo per la derivata di g(x) sostituendo poi   t con g(x).

dobbiamo invertire il processo per integrare: ovvero dobbiamo riconoscere una situazione del tipo

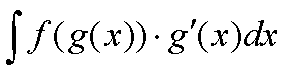
e poi fare i passaggi al contrario

Posso pensare che la primitiva sia una funzione F(t) dove dove F(T) è la primitiva di f(t) con t= g(x).  Infatti se derivo F(t) avrò  f(t)g'(x) ovvero f(g(x))g'(x).

formalmente farò

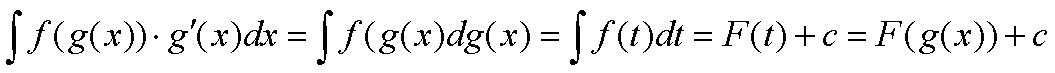
dove posso osservare  l'operazione g'(x)dx=dg(x) che è formalmente identica all'uso che facciamo del differenziale

(l'operazione verrà usata in maniera formale abbastanza spesso)