le trasformazioni affini

una trasformazione (corrispondenza biunivoca tra punti del piano) rappresentata dalle equazioni

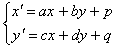
tale il determinante della matrice associata 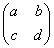sia diverso da ZERO è UNA AFFINITA' (quindi le affinità sono trasformazioni invertibili)

proprietà

1. Un'affinità trasforma rette in rette
2. Un'affinità trasforma punti non allineati in punti non allineati (conseguenza di quanto detto nel punto 1 e dell'invertibilità delle affinità) conseguenza: un triangolo viene trasformato in un triangolo, ma un triangolo equilatero non è detto che ...
3. Un'affinità conserva il punto medio (dimostrazione pag.217Vol.II-1)
4. Un' affinità trasforma rette parallele in rette parallele (conserva il parallelismo (dimostrazione pag. 217Vol.II-1) conseguenza: un parallelogramma viene trasformato in un parallelogramma, ma un quadrato non è detto che...
5. un'affinità trasforma gli estremi di un segmento negli estremi di un segmento.
6. un'affinità trasforma coniche in coniche
7. un'affinità trasforma la tangente ad una conica nella tangente ad una conica (dimostrare per assurdo: confrontare con quanto detto a pag281Vol.I punto 2 della dimostrazione).
8. un'affinità trasforma una figura di area S in una figura di area S'=S|det(A)|       

per tornare indietro usa il pulsante INDIETRO del tuo browser