IL QUANTO DI ENERGIA

IL QUANTO DI ENERGIA

Teoria di Planck

1. Concetti preliminari

Ogni corpo, sottoposto a riscaldamento, irradia calore. Questo fenomeno viene chiamato irraggiamento termico e consiste nell’emissione di onde elettromagnetiche, che si verifica ad ogni temperatura, tranne che allo zero assoluto. L’intensità dell’irraggiamento aumenta con l’aumentare della temperatura.

Per caratterizzare la radiazione emessa da un corpo qualunque, si introduce il concetto di potere emissivo spettrale. Esso rappresenta la quantità di energia elettromagnetica irradiata dal corpo per unità di superficie e per unità di tempo nell’intervallo spettrale [ν, ν+d ν]. Il potere emissivo spettrale, e_ν, è legato alla densità di energia elettromagnetica emessa, u_ν, dalla relazione:

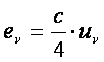dove c è la velocità della luce. (1)

La densità di energia elettromagnetica è la quantità di energia per unità di volume.

Naturalmente un corpo, oltre che ad emettere energia elettromagnetica, può anche assorbirla. L’assorbimento può essere quantificato attraverso il potere assorbente spettrale a_ν (o assorbanza spettrale), definito come la quantità di energia elettromagnetica assorbita dal corpo per unità di superficie e per unità di tempo nell’intervallo spettrale [ν, ν+d ν].

Ora, anche se ogni corpo ha un suo caratteristico potere emissivo e un suo proprio potere assorbente, tuttavia, per ogni fissata frequenza ν, il loro rapporto dipende solo dalla temperatura, secondo la legge di Kirchhoff:

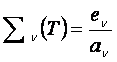(2)

Tale rapporto rappresenta, perciò, una funzione universale e non dipende dal particolare corpo considerato, ma solo dalla temperatura.

2. Il corpo nero e il suo spettro di emissione

Si intende per corpo nero un corpo capace di assorbire tutta la radiazione elettromagnetica incidente su di esso, per qualunque frequenza e per qualunque temperatura. Un corpo del genere non riflette, né trasmette radiazione.

E’ chiaro che non esistono corpi con queste caratteristiche, ma la migliore approssimazione di laboratorio a un corpo nero ideale non è una sostanza, ma una cavità. Questa cavità è costruita con pareti ottimamente isolanti, in una delle quali viene praticato un piccolo orifizio. Quando la cavità viene riscaldata, la radiazione uscente dall’orifizio è un buon campione della radiazione di equilibrio entro la cavità riscaldata, che praticamente è la radiazione di un corpo nero ideale (fig.1):

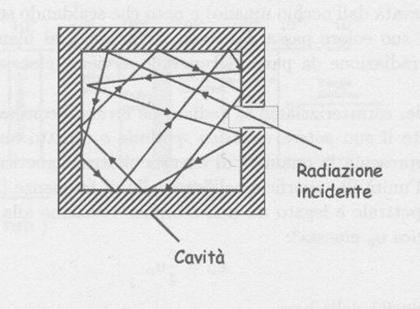(fig.1)

Dalla definizione di corpo nero segue immediatamente un potere assorbente spettrale unitario ad ogni frequenza, cioè: a_ν = 1.

Allora possiamo interpretare la legge di Kirchhoff nel modo seguente: il rapporto tra il potere emissivo e il potere assorbente di un corpo qualsiasi ad una certa frequenza e ad una certa temperatura è sempre uguale al potere emissivo del corpo nero a quella frequenza e a quella temperatura.

Da ciò scaturisce l’enorme importanza del corpo nero nella fisica. Infatti se conosciamo lo spettro di emissione del corpo nero, siamo in grado di risalire, tramite la legge di Kirchhoff, alle caratteristiche di assorbimento e di emissione di qualunque altro corpo.

Il tipico apparato sperimentale per lo studio dello spettro di emissione del corpo nero è presentato schematicamente nella fig.2:

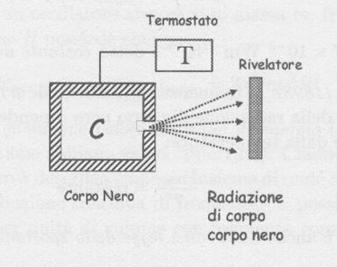(fig. 2)

La cavità C rappresenta il corpo nero le cui pareti vengono portate alla temperatura desiderata tramite accoppiamento con il termostato T . La radiazione che esce dall’orifizio viene raccolta e analizzata (sia in intensità che in distribuzione spettrale) dal rivelatore R.

Il risultato sperimentale è descritto nella fig. 3, dove viene riportata la densità di energia elettromagnetica u_ν emessa da un corpo nero a diverse temperature, in funzione della frequenza ν.

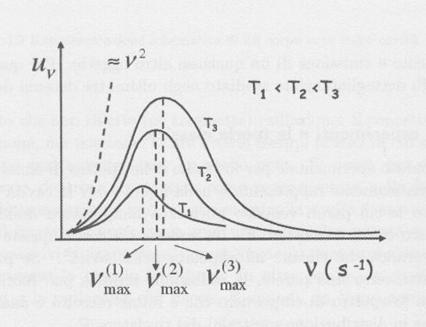fig. 3

L’analisi quantitativa delle curve sperimentali ha permesso di stabilire alcune leggi fenomenologiche:

a) Legge di Stefan: la densità totale di energia elettromagnetica u (graficamente: l’area della curva sottesa dalla funzione u_ν) è proporzionale alla quarta potenza della temperatura T del corpo nero:

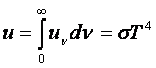(3)

b) Legge di Wien (nota anche come legge dello spostamento): la frequenza alla quale si ha il massimo dell’intensità spettrale della radiazione di corpo nero dipende in modo direttamente proporzionale dalla temperatura assoluta:

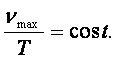(4)

3. La fisica classica non riesce a spiegare lo spettro di emissione del corpo nero.

La radiazione di corpo nero presente nella cavità deve essere in equilibrio termico con la materia che costituisce le pareti della cavità stessa. Se così non fosse, si osserverebbe un flusso di energia tra parete e radiazione e viceversa. Perciò possiamo calcolare indifferentemente la distribuzione di energia degli atomi o della radiazione. Calcoliamo quella relativa agli atomi. Gli atomi, a causa dei moti termici, oscillano come oscillatori armonici. Dalla meccanica classica sappiamo che un oscillatore armonico di massa m, con frequenza propria ν e ampiezza di oscillazione R possiede energia

E = 2π²m ν²R² (5)

[Questa formula si ricava considerando che l’energia totale E_t di un oscillatore è costante ed è in ogni istante data dalla somma dell’energia cinetica, 1/2mv² e dell’energia potenziale, ½ kx²: E_t = 1/2mv²+ ½ kx². Poiché, al massimo dell’elongazione, R, della molla l’en. cinetica è nulla, mentre quella potenziale è massima, possiamo scrivere E_t = 1/2kR². Dalla relazione 2πν = (k/m)^1/2 si ha: k =4π²ν²m.

Perciò E_t = 2 π²ν²mR²]

Questo significa che può possedere qualunque valore continuo di energia (variando opportunamente la frequenza e l’ampiezza di oscillazione). Dal punto di vista classico, quindi, la radiazione di corpo nero è descritta come un insieme di onde stazionarie confinate nella cavità con distribuzione continua di frequenze. Perciò il problema della distribuzione dell’energia tra le varie frequenze si riduce apparentemente alla determinazione del numero di vibrazioni permesse (e quindi di onde elettromagnetiche) in ogni intervallo di frequenza.

E’ possibile calcolare il numero dn_ν di onde per unità di volume con frequenza compresa tra ν e ν + dν è:

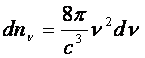(6)

Alle quali corrisponde un’energia media per unità di volume, alla temperatura T e nell’intervallo spettrale [ν,ν + dν] pari a:

u_νdν = E_mdn_ν = k_BTdn_ν(7)

dove abbiamo fatto uso del principio di equiripartizione dell’energia, imponendo che l’energia media valga all’equilibrio k_BT (k_Bè la costante di Boltzmann). Combinando le due equazioni si ottiene:

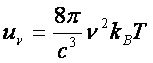(8)

Nota come legge di Rayleigh-Jeans.

Nella fig. 3 è riportato l’andamento di u_ν previsto dalla legge di Rayleigh-Jeans (linea tratteggiata). Il confronto tra questo e le curve sperimentali (linee piene) evidenzia il disaccordo completo tra una legge dedotta applicando i concetti della fisica classica e i risultati sperimentali. Il modello di Rayleigh-Jeans (8), infatti, non prevede l’esistenza di un massimo per u_ν che, addirittura, cresce in modo monotono fino a divergere a frequenze elevate. La conseguenza di ciò è importante: integrando la (8) su tutto lo spettro, si ottiene un risultato infinito, del tutto differente dalla legge sperimentale di Stefan (equazione 3). Questo risultato così stridente con la realtà fu chiamato catastrofe ultravioletta. Inoltre la (8) contrasta col principio di conservazione dell’energia. Infatti basterebbe scaldare un corpo ad una temperatura diversa dallo zero assoluto per emettere una quantità infinita di energia.

4. Il quanto di energia

La meccanica classica era fondata sull’antica massima “natura non facit saltum”.Così si poteva prevedere che un oscillatore acquistasse energia in modo continuo con incrementi arbitrariamente piccoli. Benché si pensasse che la materia fosse atomica (discontinua, discreta), si ammetteva che l’energia fosse perfettamente continua. Planck rifiutò questo concetto e suggerì che un oscillatore potesse acquistare energia solo per unità discrete, chiamate quanti. La teoria quantistica cominciò perciò come una teoria atomica dell’energia. La grandezza ε del quanto, o atomo, di energia non era fissata, ma dipendeva dalla frequenza dell’oscillatore:

ε = hν (9)

dove h è la costante di planck. Nel Sistema Internazionale h = 6,6262 x 10^-34 J·s.

5. legge di distribuzione di Planck

Consideriamo ora un insieme di N oscillatori aventi una frequenza di vibrazione fondamentale ν. Se questi possono acquistare energia solo per incrementi di hν, le energie permesse sono 0, hν, 2hν, 3hν, …….Ora secondo la formula di Boltzmann se N_o è il numero di sistemi nello stato più basso di energia, il numero N_i di sistemi che possiede un’energia superiore di ε_ia quella dello stato fondamentale è data da

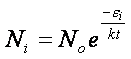
Nel caso degli oscillatori possiamo scrivere, per esempio:

……………

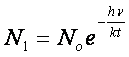
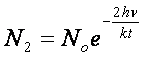
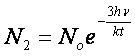
Il numero totale degli oscillatori in tutti gli stati energetici è perciò:

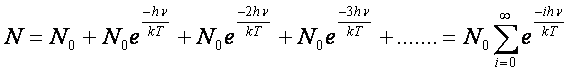
L’energia di tutti gli oscillatori è uguale all’energia di ciascun livello per il loro numero in quel livello:

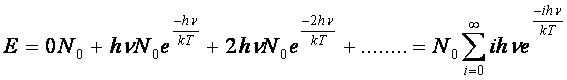
L’energia media di un oscillatore è perciò:

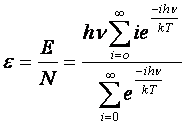(9)

La serie di potenze al denominatore (serie geometrica) ha per somma 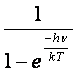(essendo <1), mentre la serie al numeratore ha per somma:

Perciò la (9) diventa:

Usando questa espressione dell’energia quantizzata al posto dell’espressione classica dell’energia di un oscillatore, ε = kT, nella (8), si ha:

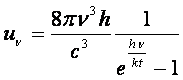(10)

Questa formula è in ottimo accordo con la curva sperimentale (fig.3). Infatti:

· il limite per frequenze infinite è zero

· il limite per frequenza nulla è zero

· il limite per frequenze piccole è u_ν≈ ν², in accordo con la teoria di Rayleigh-jeans

· ammette un massimo per una certa frequenza ν_max, che dipende linearmente dalla temperatura T

· Il grafico della funzione (10) è del tutto sovrapponibile alle curve sperimentali su tutto lo spettro delle frequenze.

Torna a ARGOMENTI DI CHIMICA FISICA