Torna a    ARGOMENTI DI CHIMICA FISICA

 

 

 

ENERGIA LIBERA ED EQUILIBRIO CHIMICO NELLE REAZIONI IN FASE GASSOSA

 

 

Da una delle equazioni fondamentali che esprimono i differenziali delle funzioni termodinamiche

 

                                                       

 

Si ricava, per un processo infinitesimo che avviene a temperatura costante,

 

                                                                        (1)

 

Ma, essendo per la legge di stato dei gas ideali,

 

                                                           

 

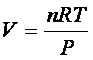
la (1) diventa

                                                         

 

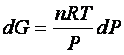
o anche                                          

                                                             (1 a)

 

 

La variazione di energia libera in una trasformazione finita tra gli estremi G0e P0, che rappresentano l’energia libera e la pressione in uno stato standard opportunamente scelto e i corrispondenti valori in qualunque altro stato G e P è ottenuta  integrando ambo i membri della (1 a):        

 

                                                    

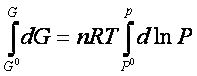
Da cui   si ottiene:.

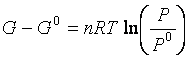                                                        (2)

 

Poiché per la pressione si è scelto come stato standard il valore P0 = 1atm, l’equazione  (2)  diventa:          

 

                                                          (3)

 

 

 

Questa equazione indica la variazione di energia libera che un gas subisce nel passaggio dalla pressione  di 1 atm nello stato standard , al valore generico P finale.

 

Ora se consideriamo una miscela di gas, ciascuno dei quali possiede una pressione parziale pi, la (3) può essere applicata ad ogni componente iesimo della miscela:          .       

                                               

 

Consideriamo una reazione in fase gassosa: νa A  + νb B                νc C  +  νd D

 

 La variazione ΔG che accompagna questa reazione   è

 

                                                            (4)

 

dove ΔGi sono le variazioni delle energie libere dei gas e i coefficienti stechiometrici υ dei reagenti sono presi col segno negativo.

 

Sapendo però che la variazione di energia libera di ogni componente gassoso è data dalla (3), la (4) può essere scritta nel seguente modo:                              

 

                                               (4 a)

 

Se la reazione giunge all’equilibrio, ΔG =0, perciò la (3) diventa:  

 

                                                 ,

 

cioè:

 

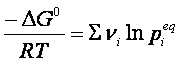                                                     (5)

 

 

Nella quale si vede che a temperatura costante, il primo membro deve essere costante, essendo ΔG0 indipendente dalla temperatura. Perciò lo sarà anche il secondo membro dell’espressione, che, per la proprietà dei logaritmi,  può essere scritto nel seguente modo:

 

                                       

 

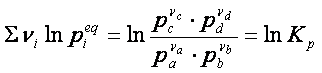
Dove Kp è la costante di equilibrio in funzione delle pressioni parziali dei componenti gassosi. In definitiva la (5) diventa:

 

 

                                          

 

 

Se è nota la variazione di energia libera standard della reazione, passando dai logaritmi ai numeri si ottiene il valore della costante di equilibrio in funzione delle pressioni parziali  della reazione

                      

                                               

 

 

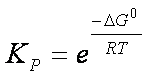
Torna a    ARGOMENTI DI CHIMICA FISICA