I pneumatici sono l'elemento più importante che determina la guidabilità della macchina, in quanto sono l'unico punto di collegamento tra la macchina ed il terreno. Dato che la tenuta dipende soltanto dall'attrito tra la superficie del terreno e la porzione del pneumatico che tocca terra, esaminiamo ora le leggi che regolano il fenomeno dell'attrito.

1.1 L'attrito

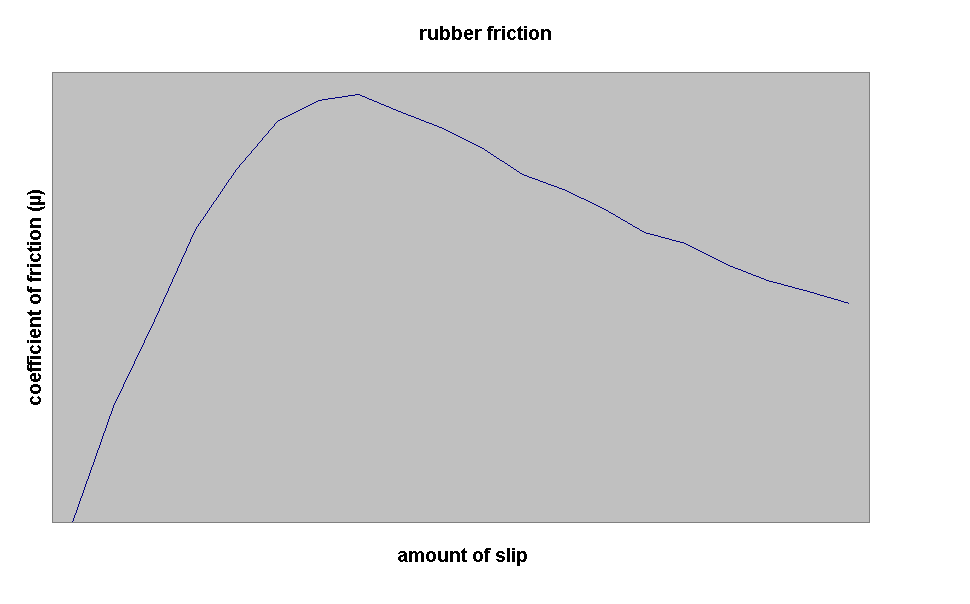
Sull'asse orizzontale troviamo l'ammontare dello slittamento del pneumatico sul terreno, dallo 0% (non c'è slittamento, si ha un rotolamento puro della ruota sul terreno) al 100% (la ruota è ferma mentre il veicolo è in movimento (frenata), o viceversa ("sgommata")). Sull'asse verticale è riportato il coefficiente di attrito corrispondente. Nella zona a sinistra del grafico, si ha lo scorrimento del materiale all'interno del pneumatico. Ciò accade quando la gomma si deforma sotto sforzo, e la zona di contatto col terreno si sposta rispetto all'asse. Questo spostamento dà origine ad un "angolo di slittamento". Nella parte destra del grafico, l'effetto dominante è lo slittamento tra le due superfici, ed il pneumatico comincia a slittare un poco anche lateralmente. Si noti che m raggiunge il suo valore massimo quando c'è un po' di slittamento, tipicamente tra il 5% ed il 15%. Ciò è dovuto alla particolare interazione tra la gomma ed il terreno.

In effetti, la ragione per cui il grafico ha questo strano andamento è che ci troviamo di fronte a più fenomeni concomitanti: ci sono infatti due distinti meccanismi in atto, aderenza e isteresi.

Il primo effetto, l'aderenza, è dovuto al contatto tra le molecole periferiche della gomma e della superficie del terreno. La gomma è un polimero, e la sua struttura molecolare assomiglia ad un piatto di spaghetti, mentre la superficie del terreno è per lo più di tipo cristallino, in cui gli atomi sono disposti in modo molto più compatto. Quando vi è una differenza di velocità tra le due superfici, gli "spaghetti" di atomi della gomma tendono ad allungarsi. Alcuni legami molecolari si romperanno, altri se ne formeranno, e questo processo continuerà fintanto che una superficie viene trascinata sull'altra. Ovviamente, questo processo richiede energia, e una forza, che è la forza di aderenza. Questa forza raggiunge il massimo valore quando la velocità relativa è tra 0,03 e 0,06 m/s.

Il secondo effetto, l'isteresi, è dovuto alla deformazione della gomma. Nella distorsione della forma della carcassa, in alcune zone la gomma viene compressa, in altre viene stirata. Perché possa avvenire questa deformazione, gli atomi devono muoversi gli uni rispetto agli altri, e questo è un processo irreversibile, come sempre, a causa dell'attrito. L'attrito causerà un riscaldamento del pneumatico, e, ancora una volta, ciò richiede energia, e quindi una forza. Questa forza è la forza di isteresi, che è molto simile alla forza di aderenza, solo che è determinata dall'attrito interno nel materiale del pneumatico.

La proporzione tra queste due componenti cambia al variare della forza verticale esercitata sul pneumatico e dell'ammontare dello slittamento. Ad esempio, se c'è più slittamento, la componente di isteresi sarà dominante rispetto a quella di aderenza. Se la mescola è molto morbida, la temperatura è alta e la superficie è liscia, la forza dominante sarà quella di aderenza.

Si noti che tutto ciò è valido quando la superficie del terreno è molto dura, come asfalto o argilla molto compatta. Se la superficie non è dura, è la deformazione della superficie stessa che dà luogo alla forza di attrito: i tasselli del pneumatico penetrano nella superficie, scavandovi dei solchi. In tal caso, il grafico non ha una porzione discendente: m cresce sempre all'aumentare del carico verticale sul pneumatico e dello slittamento. E' un meccanismo totalmente differente. Questa è anche la ragione per cui le macchine da strada perdono in direzionalità quando, nell'affrontare una curva, il peso si trasferisce sulle ruote esterne, mentre per una macchina per fuoristrada accade esattamente il contrario. Per questo motivo, è sensato che macchine da strada abbiano un'alta rigidità al rollio (si pensi alle barre anti-rollio), al contrario di quelle per fuoristrada.

1.2 Il cerchio di tenuta

Ora che sappiamo come funziona l'attrito, e come di solito sia massimo quando c'è un po' di slittamento, vediamo come influenza il comportamento di guida della macchina.

A meno che la scolpitura del penumatico non sia asimmetrica, l'attrito è lo stesso in tutte le direzioni, e anche il suo valore massimo è lo stesso in tutte le direzioni. Questo fatto può essere rappresentato dal cerchio di tenuta.
 

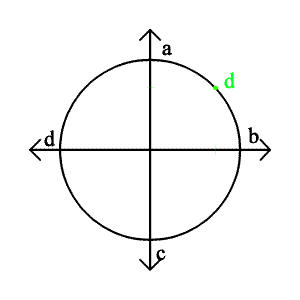
La componente verticale del grafico rappresenta l'accelerazione e la decelerazione, mentre la componente orizzontale rappresenta la sterzata a destra e a sinistra. Il massimo valore di tenuta (grip) si ha sulla circonferenza del cerchio, e l'area del cerchio stesso rappresenta il valore totale dell'attrito tra il pneumatico e la strada.

Ovviamente, per ottenere i tempi migliori bisogna sfruttare i pneumatici fino al loro limite massimo. Quindi, per frenare nel minor spazio possibile, bisognerà far lavorare i pneumatici sul punto C del grafico. Se la frenata è troppo violenta, e si oltrepassa il punto C, le ruote slitteranno, e la distanza di arresto aumenterà. Stessa cosa per l'accelerazione: se si oltrepassa il punto A, le ruote slitteranno molto e l'accelerazione sarà minore. E' anche possibile oltrepassare i limiti di tenuta durante una curva (punti D e B), e andare in testa-coda.

Ma la parte più difficile da valutare non sono gli assi, bensì i punti intermedi del grafico. Il punto d, per esempio, rappresenta una situazione in cui la macchina sta curvando a sinistra e accelerando. Si noti che d si trova sulla circonferenza del cerchio, eppure la macchina non sta né accelerando né curvando alla velocità massima, bensì ad una intermedia. Supponiamo di star accelerando quanto più possibile (punto A), quando si sterzano leggermente le ruote a sinistra. Sul grafico, ciò significa che ci si viene a trovare in un punto a sinistra di A, ovvero fuori dal cerchio, quindi le ruote perderanno la presa sul terreno, e la macchina non curverà (trazione anteriore) oppure andrà in testa-coda (trazione posteriore). Un altro fatto degno di nota è che per ottenere la massima direzionalità, non dovrebbe essere applicata alcuna potenza alle ruote (punti B e D). Per converso, per ottenere la massima accelerazione possibile, le ruote dovrebbero essere perfettamente dritte.

Si tenga a mente che il raggio del cerchio di tenuta rappresenta la massima forza di aderenza, che a sua volta è proporzionale (beh, all'incirca, come spiegato al paragrafo precedente) al carico verticale esercitato sulla ruota. Quindi, per farla breve: il raggio del cerchio cresce al crescere della forza verticale esercitata sul pneumatico, e decresce al decrescere di quella. Il cerchio smette di esistere quando non c'è alcuna pressione sul pneumatico. Ciò ha senso, in quanto una ruota appesa in aria non può resistere ad alcuna forza laterale.

1.3 L'angolo di slittamento

Forse vi sarete chiesti cosa esattamente accada quando si esce dal cerchio di tenuta, e come reagisca di conseguenza la macchina. Il concetto di angolo di slittamento consente di descrivere chiaramente cosa succede in tali circostanze.

L'angolo di slittamento è l'angolo tra la direzione in cui punta il pneumatico e la direzione in cui esso effettivamente si sta muovendo. Un pneumatico che non sta slittando ha un angolo di slittamento pari a zero.

La figura seguente rappresenta una macchina che sta percorrendo una curva a bassa velocità. Tutti e quattro gli angoli di slittamento sono nulli.

Nell'ipotesi che la macchina abbia il corretto effetto Ackermann e che le ruote posteriori abbiano convergenza neutra, la macchina può percorrere la curva senza che alcun pneumatico slitti. Si noti che le linee immaginarie (beh, non poi così immaginarie, dal momento che le ho disegnate per voi) che prolungano i semiassi si intersecano tutte in un punto. Questo è il punto intorno al quale la macchina sta curvando, diciamo il centro della curva che la macchina sta percorrendo.
Questa è la tipica situazione in cui la velocità in curva è bassa, e tutti i pneumatici sopportano grosso modo lo stesso peso.

Ma... sfortunatamente, le cose non stanno sempre come vorremmo. Una delle condizioni che si verificano comunemente è il cosiddetto sottosterzo. Questa è la condizione in cui sui pneumatici anteriori non insiste un peso sufficiente, ed essi cominciano a slittare, creando un angolo di slittamento.

L'angolo di slittamento dei pneumatici anteriori è l'angolo tra le linee blu e quelle verdi.

La macchina non sta girando attorno al punto che vi aspettereste, o che vorreste (punto N, intersezione delle linee blu). Invece, sta girando attorno al punto di intersezione delle linee verdi (punto U), il che si tramuta in un aumento del raggio di sterzata rispetto a quanto ci si aspetta. Questo è il fenomeno del sottosterzo: quando il raggio di sterzata è maggiore di quello che vorreste.

Può anche accadere il contrario: può essere insufficiente il peso esercitato sui pneumatici posteriori, che quindi cominciano a slittare. Questa situazione in genere porta alla condizione che si definisce di sovrasterzo, in cui il raggio di sterzata è minore di quello atteso.

Qui, i pneumatici posteriori hanno cominciato a slittare, dando luogo a due angoli di slittamento relativi al retrotreno. Anche il pneumatico interno anteriore ha cominciato a slittare, e questo accade perché la macchina non può girare intorno a due punti contemporaneamente. In questo caso, la macchina sta girando attorno al punto O (mentre ci saremmo aspettati che girasse attorno al punto N). In curva, le linee che definiscono gli angoli di slittamento si intersecano sempre nel punto intorno al quale la macchina sta girando. Se così non fosse, il pneumatico che sopporta il carico minore (in questo caso l'anteriore interno) seguirà un angolo di slittamento (in modo da soddisfare la condizione N.d.T.).

Si noti che il punto (O) attorno al quale la macchina sta girando è ora molto più vicino alla mezzeria della macchina ed è spostato in avanti. La macchina percorrerà una curva molto più stretta, curverà molto di più e prima di quanto atteso.

Condizioni di puro sovra- o sottosterzo sono molto comuni, ma in realtà può accadere ogni sorta di combinazioni "strane": ad esempio, è possibile percorrere la curva in derapata.

Nonostante le ruote anteriori siano sterzate a sinistra, la macchina sta percorrendo una curva a destra (in controsterzo). I pneumatici posteriori stanno slittando ad un angolo molto pronunciato.
Inutile dire che ciò richiede grande abilità di guida.

Vai al prossimo Capitolo

Vai all'Indice