Caratteristiche di un onda
Fronte d’onda
Si definisce fronte d’onda, il luogo dei punti caratterizzati dall’avere in ogni istante lo stesso valore dello spostamento dalla posizione di equilibrio.
La forma che assume la superficie del fronte d’onda è anche detta superficie d’onda.
A seconda della forma che può assumere la superficie d’onda, possiamo avere:
Onda piana, cioè un onda in cui il fronte è una superficie piana perpendicolare alla direzione di propagazione dell’onda.
Onda circolare, cioè un onda la cui superficie d’onda è una circonferenza che va allargandosi al propagarsi dell’onda.
Onda sferica, cioè quando la superficie d’onda sono delle sfere, questo è il caso di onde che si propagano nello spazio.
La direzione lungo la quale un onda si propaga è detta raggio dell’onda ed è definita come la semiretta uscente dalla sorgente e perpendicolare alla superficie del fronte d’onda.
A seconda del modo in cui le onde possono propagarsi possiamo avere:
onde trasversali, quando la direzione della vibrazione (o perturbazione) è perpendicolare a quella di propagazione del fronte;
onde longitudinali, quando la direzione della vibrazione (o perturbazione) è parallela a quella di propagazione del fronte.
Esistono anche onde nelle quali le particelle del mezzo subiscono spostamenti sia longitudinali che trasversali (come ad es. le onde marine).
Onde periodiche
Una perturbazione ondosa si dice periodica, quando un elemento della perturbazione si ripete ad intervalli regolari di tempo.
Le onde periodiche sono formate da creste e da ventri.
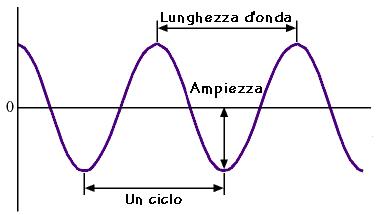
La distanza tra due creste successive (o due ventri) si chiama lunghezza d'onda e si indica con il simbolo λ.
Quando l'onda si propaga, i punti investiti dall'onda si muovono oscillando. Lo spostamento massimo di un punto dalla sua posizione di equilibrio si chiama ampiezza dell'onda e si indica con il simbolo A.
La figura mostra lo spostamento dei punti di un mezzo elastico in un determinato istante di tempo, quando sono raggiunti da un tipo particolare di onda periodica detta sinusoidale.
f = 1/T
f frequenza (Hz)
v=λ/T
λ lunghezza d'onda (m)
T periodo (s)
v= λ f
v velocità dell'onda (m/s)
A ampiezza dell’onda (m)
La frequenza dell'onda indica quante volte in un punto del mezzo elastico passa una cresta (o un ventre) in un secondo. Essa si indica con il simbolo f.
Il periodo T dell'onda è l'intervallo di tempo che intercorre tra il passaggio di due creste successive (o di due ventri) per lo stesso punto. Appare evidente che la frequenza è il reciproco del periodo.
In un periodo l'onda percorre una distanza pari alla lunghezza d'onda. Quindi la velocità è il rapporto tra la lunghezza d'onda e il periodo, se l'onda si sta propagando in un mezzo omogeneo a velocità costante.
Il periodo e la frequenza dell'onda sono determinati dalle caratteristiche della sorgente che l'ha generata.
La velocità è determinata dalle caratteristiche del mezzo in cui l'onda si propaga.
La relazione v = λ f è chiamata relazione fondamentale delle onde o legge di propagazione di un’onda.
Onde armoniche semplici
Onde sinusoidali
L'ampiezza dell'onda dipende sia dalla sorgente, sia dal tipo di onda generato, sia dalle caratteristiche di elasticità del mezzo di propagazione.
Consideriamo una sorgente che, muovendosi di moto armonico di ampiezza A, generi onde meccaniche in un mezzo perfettamente elastico ed esaminiamo vari casi:
a) se le onde sono lineari come in una corda l'ampiezza
dell'onda è quella del moto armonico della sorgente.
b) se le onde sono circolari come quelle prodotte da una punta vibrante
sull'acqua, o sferiche, come quelle del suono, l'ampiezza dell'onda diminuisce
con la distanza dalla sorgente.
Se la sorgente oscilla di moto armonico, l'onda generata è sinusoidale e può essere descritta matematicamente da una sinusoide.
Nelle onde sinusoidali l'ampiezza dell'onda varia in modo sinusoidale nel tempo e nello spazio. Questo tipo di onde riveste un'importanza particolare perché ogni altra forma d'onda periodica può essere ottenuta come sovrapposizione di onde sinusoidali (Teorema di Fourier).
Equazione d’onda
Si consideri una particella P mobile lungo una circonferenza in moto uniforme (vedi Figura). Se si osserva lo spostamento della sua ombra Q lungo il diametro, si può notare che Q compie un moto oscillatorio intorno al centro O della circonferenza. Se immaginiamo poi che questa circonferenza può essere pensata come il cerchio trigonometrico, allora notiamo che Q descrive lo spazio come il coseno dell’angolo a che varia in funzione del tempo t.
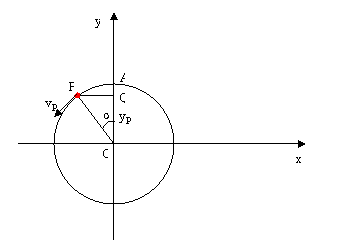
OQ = yP(t)
yP = A·cos a
a(t) = w·t
yP(t) = A·cos (w·t )
A = yPmax è l’ampiezza massima, che corrisponde al raggio della circonferenza.
w = 2·p/T = 2·p·f
w (omega) è la pulsazione
Fase di un onda
In generale l’equazione d’onda è scritta come:
y = A·cos (w·t - j)
La grandezza j rappresenta la fase dell’oscillazione della sorgente.
Si definisce fase dell’oscillazione la frazione del periodo già trascorsa all’istante in cui ha origine il tempo (q/T). Il valore angolare della fase è espresso come: j = (2·p/T)· q
q è il tempo di anticipo dell’onda.
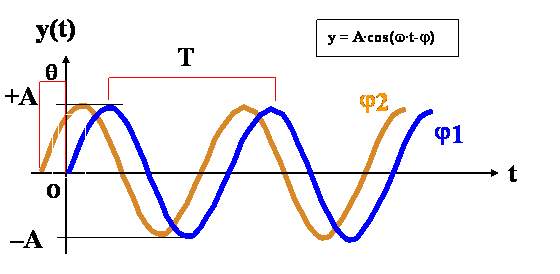
Le due onde sopra hanno stessa ampiezza, stessa pulsazione,
ma hanno fasi diverse.
Energia trasportata da un onda
Come già detto in precedenza un onda trasporta energia. Tale energia, se non ci sono perdite nel mezzo di propagazione, si conserva.
Il tipo di energia trasportata, nel caso di onde meccaniche, è energia meccanica.
L’energia meccanica di un sistema è la somma dell’energia cinetica e dell’energia potenziale di un punto del mezzo che subisce oscillazioni armoniche:
![]() V è la
velocità del punto che oscilla di moto armonico
V è la
velocità del punto che oscilla di moto armonico
![]()
![]()
In definitiva si ottiene che l’energia trasportata da un onda è proporzionale all’ampiezza al quadrato. Se l’ampiezza diminuisce, diminuisce anche l’energia dell’onda.
Intensità di un onda
Si definisce intensità dell’onda l’energia trasportata nell’unità di tempo attraverso l’unità di superficie.
![]() l’unità di misura è
l’unità di misura è
![]()
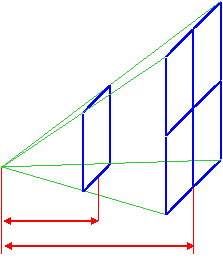
Nel caso di onde sferiche in cui S = 4·p·r2 si ha:
![]()
Dato che l’energia è costante (principio di conservazione dell’energia), l’intensità diminuisce con il quadrato della distanza. Nel caso particolare in cui la superficie d’onda dovesse mantenere inalterata la sua dimensione, l’intensità sarebbe indipendente dalla distanza dalla sorgente. Questo è il caso di propagazione di un onda lungo una corda.
Principio di sovrapposizione
Una delle caratteristiche fondamentali della propagazione ondosa è il comportamento espresso dal principio di sovrapposizione: quando due onde si incontrano, si sovrappongono, cioè le loro ampiezze si sommano algebricamente, dopo di che proseguono, nel loro verso di propagazione, con le stesse caratteristiche che avevano prima di incontrarsi.
Questo significa che se ognuna di esse provocasse in un punto uno spostamento, la prima S1 e la seconda S2 il punto considerato sarebbe sottoposto a uno spostamento S = S1+ S2