
|
|
22-09-05
|
Per meridiana orizzontale si intende un piano orario orizzontale ad una certa latitudine, diversa dal polo o dall'equatore.
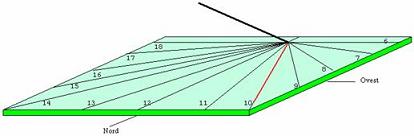
Fig. 1
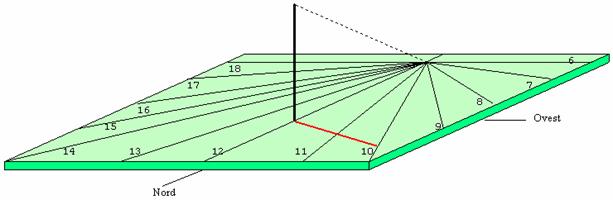
La meridiana orizzontale si presenta come in figura. Il sole sorge ad Est ( a sinistra della figura) e proietta l’ombra dello stilo sulla destra dell’orologio solare. A mezzogiorno l’ombra verrà invece proiettata esattamente verso il Nord, sovrapponendosi alla linea delle ore 12 , (linea meridiana) , il pomeriggio l’ombra verrà invece proiettata sulla sinistra dell’orologio. Lo stilo , esattamente sovrapposto alla linea meridiana delle ore 12 formerà con il piano orario un angolo ben preciso. Per ottenere la funzione calendario, qui tralasciata, la lunghezza dello gnomone deve avere una ben precisa lunghezza. In questo caso l'ora si legge per sovrapposizione di tutta l'ombra sulla linea oraria. Nell'esempio sono le ore 10.
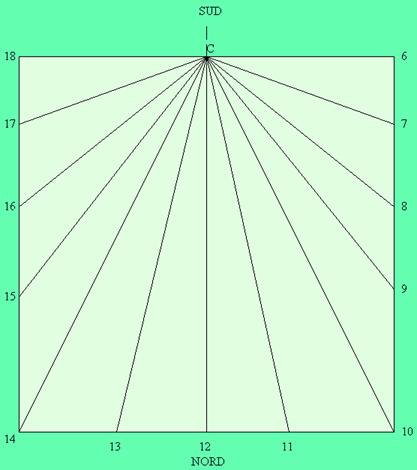
Fig. 2
La linea meridiana (ore 12) è asse di simmetria . Gli angoli formati dalle linee orarie con questa linea sono uguali fra loro come segue:
11 = 13 10 = 14 9 = 15 8 = 16 7 = 17 6 = 18 5 = 19
Questi angoli dipendono dalla latitudine del luogo in cui l’orologio solare orizzontale verrà collocato. VLo gnomone forme con il piano orario un angolo pari alla latitudine.
Dalla meridiana equinoziale alla meridiana orizzontale.

Fig. 3
Eq è la meridiana equinoziale equiangolata di 15°, mentre Or è una meridiana orizzontale, ma essendo posta su un'altra parallelo (latitudine) è inclinata rispetto a Eq, come si evince dal disegno. Le linee orarie di Or come si andrà a dimostrare non saranno equiangolate come al polo nord, o parallele come all'equatore.
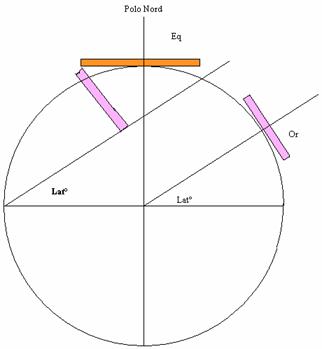
Fig. 4
La meridiana orizzontale posta a latitudine Lat° può essere spostata fino a che uno dei suoi lati coincida con la meridiana equinoziale. L’angolo di Lat° che lega le due meridiane rimane invariato. Dalla figura precedente si esalta ora in forma tridimensionale (assonometria) ciò che interessa. Della meridiana equinoziale vengono considerate solo un paio di linee orarie.
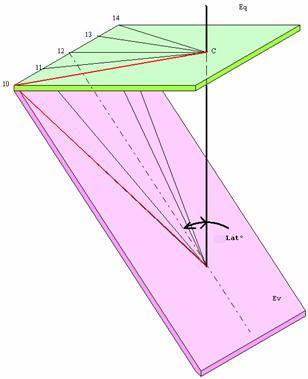
Fig. 5
Se un fascio di luce proietta l’ombra(rossa) dello gnomone superiore verso il punto 10, anche l’ombra dello gnomone inferiore proietterà l’ombra verso tale punto. Ovvero se immaginiamo le linee orarie della meridiana equinoziale come fessure, ed un fascio di luce ad esse perpendicolari otterremo le linee orarie inferiori. A questo punto si possono stabilire i punti comune alle due meridiane. Esse sono :
L’angolo Lat° di angolazione dei due piani sempre rimasto inalterato.
I punti orari 10,11,12,13 e 14 che sono comuni ai due piani .
L’altezza dello gnomone inferiore ,meridiana orizzontale.
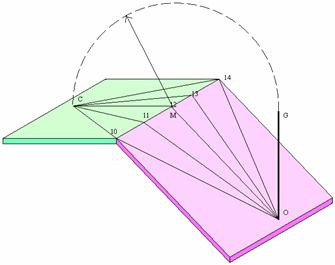
Fig. 6
La figura precedente con il piano orario sottostante spostato. Provvediamo ora a porre i due piano orari sullo stesso piano, ruotiamo cioè verso l’alto la meridiana orizzontale viola dagli angolo orari sconosciuti.
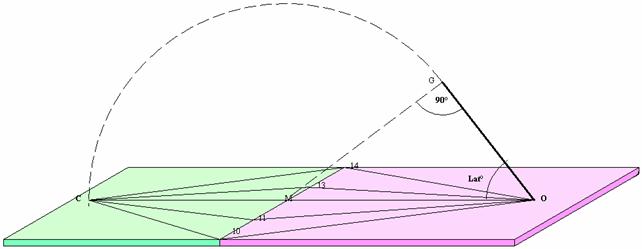
Fig. 7
Ed ecco il risultato. Quella verde è sempre la meridiana equinoziale equingolata di 15°, quella viola la meridiana orizzontale posta a Lat° j° di cui sono ancora sconosciute le formule.
Notiamo che lo gnomone forma come prima un angolo pari alla latitudine, ma è necessario soffermarsi sull’angolo formato fra la punta dello gnomone ed il punto M. Esso e retto. Lo abbiamo già evidenziato nelle tavole precedenti.
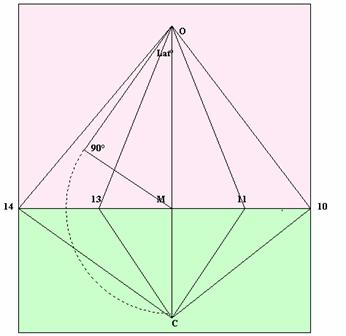
Fig. 8
La figura assonometrica precedente vista in piano. Lo gnomone è stato coricato sul piano orario , continuando a formare con l’asse C1-M un angolo pari alla Lat°. Anche l’asse C1-M ha la sua lunghezza ben definita e che risale alle prime figure.
Dalla figura alla formula. ( Il precedente punto C1 è stato ridenominato O)
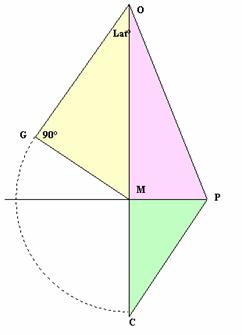
Fig 9
IPOTESI:
MOG^= Lat°
GM = CM
Gli angoli aventi origine in C sono uguali fra loro (15°) .
w° = angolo orario avente origine in O
p° = angolo al polo (Multiplo di 15°)
TESI
Tan w° = tan p° * sen Lat°
GM = OM * sen Lat°
MC=GM= OM * sen Lat°
MD= MC * tan p° = OM * sen Lat° * tan p°
Tan w° = MD / OM = OM * sen Lat° * tan p° / OM° = sen Lat° * tan p°
Tan w° = tan p° * sen Lat°
La meridiana orizzontale – Costruzione geometrica usuale.
Scelto un piano orario quadrato (marmo, legno o altro) , si traccia su di esso la linea meridiana (ore 12) OC.
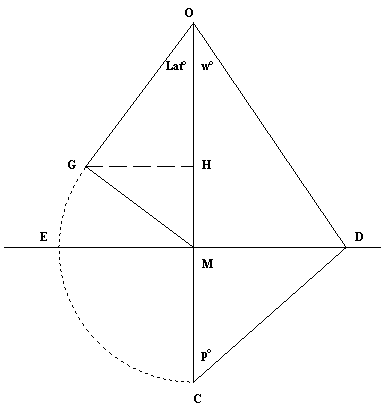
Fig. 10
Si traccia la retta OG di lunghezza pari allo gnomone e la si riporta sul piano angolata rispetto a OC di un angolo pari alla latitudine. Si cerca il punto M tenendo presente che l’angolo OGM^= retto, o se si preferisce GME^=Lat°
Si punta il compasso in M con apertura MG e si trova C. Da C dipartono gli angoli orari equinoziali multipli di 15° che intercettano la retta ED.
Se l’angolo p° = 7,5° avremo il punto orario delle 11.30 se verso D le 12.30 se verso E
Se l’angolo p° = 15° avremo il punto orario delle 11 se verso D le 13 se verso E
Se l’angolo p° = 23,5° avremo il punto orario delle 10.30 se verso D le 13.30 se verso E
Se l’angolo p° = 30° avremo il punto orario delle 10 se verso D le 14 se verso E
……………………………………………..
…………………………………………….
Si tracciano quindi le rette orarie con origine in O e passanti per questi punti.
In figura se p° = 30° OD è la retta delle ore 10 se 45° sarà invece la linea oraria delle ore 9.
Stilo ortogonale. E’ uguale all’altezza GH ed è infisso in H. L’ora si legge con la sola punta dell’ombra, e non per sovrapposizione dell'ombra come in fig.1. Solitamente (per maggiore robustezza) si usa un triangolo di metallo uguale al triangolo OGH.
La funzione calendario e le line di declinazione.
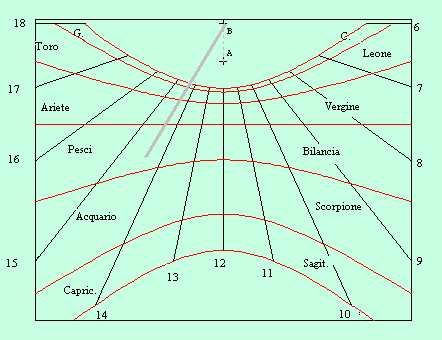
Orologio solare orizzontale con curve di declinazione diurne. Sono quasi le 14.30, il sole si trova in pesci o in in Bilancia.
Ultimo aggiornamento: 22-09-05