MODELLI di geometria non euclidea
Geometria Iperbolica
 | Modello di Klein-Beltrami
Il piano iperbolico è costituito dai punti interni di un cerchio [orizzonte]
Le rette sono le corde del cerchio.
La metrica prevede formule (basate sul logaritmo di birapporti) sia per la
misura delle distanze che degli angoli.
Non essendo il modello conforme, non si possono valutare ad occhio le
relazioni metriche tra i segmenti o gli angoli.
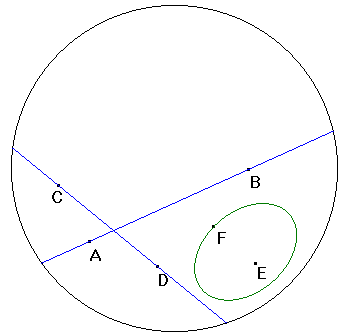
In questa immagine ci sono due rette di colore blu e un cerchio di
colore verde. Si noti come il cerchio sia in realtà rappresentato da
un'ellisse.
È più lungo il segmento AB o CD ?
|
 | Disco di Poincaré
Il piano iperbolico è costituito dai punti interni di un cerchio [orizzonte]
Le rette sono archi di cerchio ortogonali all'orizzonte
I segmenti sono misurati come nel modello precedente, mentre gli angoli sono
misurati secondo la normale metrica euclidea [si tratta di angoli tra archi
di cerchio]. Data questa caratteristica, il modello si presta facilmente ad
illustrare le relazioni angolari in geometria iperbolica, e per questo è
molto usato.
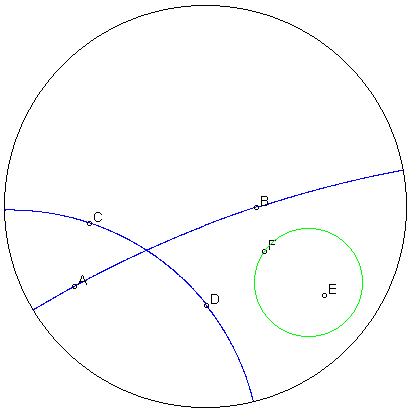
In questa immagine ci sono due rette di colore blu
e un cerchio di colore verde. Si nota che il centro E del cerchio non si
trova dove ci si aspetterebbe.
Il cerchio però è come ci si aspetta, perché questo è un modello
'conforme'.
|
 | Semipiano di Poincaré
Il piano iperbolico è costituito da un semipiano.
Le rette sono semicerchi centrati sulla retta sostegno del semipiano o
semirette ad essa perpendicolari.
Anche questo modello conserva la misura euclidea degli angoli.
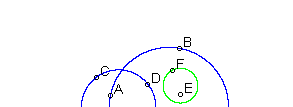 In
questa immagine ci sono gli stessi elementi della figura precedente,
rappresentati in questo diverso modello. In
questa immagine ci sono gli stessi elementi della figura precedente,
rappresentati in questo diverso modello. |
Geometria Ellittica
 | Disco di Klein
Il piano ellittico è rappresentato dall'interno di un cerchio e dalle
coppie di punti antipodali sulla circonferenza.
Le rette sono i diametri o gli archi di cerchio che incrociano l'orizzonte
agli estremi di un diametro.
Il modello è conforme, cioè conserva la misura euclidea degli angoli.
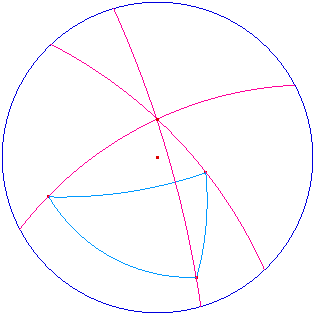
L'immagine mostra un triangolo azzurro con le tre altezze rosse. Le
altezze come si vede si incontrano in un punto.
Misurando gli angoli del triangolo si trova che la loro somma supera 180° .
|
 | Sfera di Riemann
Il piano ellittico è rappresentato dalle coppie di punti antipodali su una
superficie sferica [due punti antipodali sono lo stesso punto ellittico].
Le rette sono i circoli massimi della sfera.
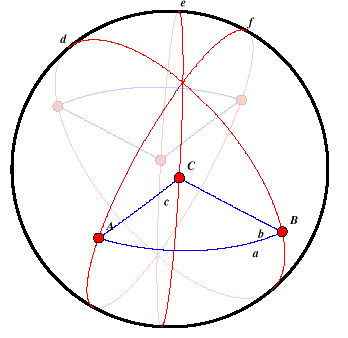
Così appare la figura precedente in questo modello. |
|