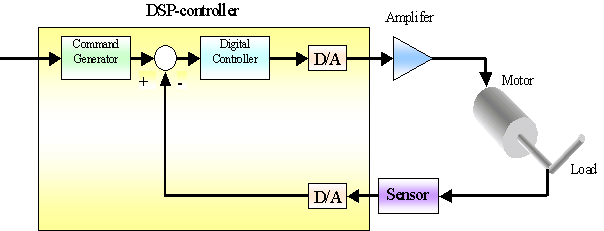
Figura 1
Fino a pochi anni fa, i motori asincroni erano connessi direttamente alla rete o controllati mediante il metodo scalare V/f. Quando si progetta una regolazione di velocità, questi metodi presentano seri inconvenienti in termini d’efficienza e realizzabilità del pilotaggio. Col primo metodo non si può realizzare una variazione di velocità, e le prestazioni del sistema dipendono molto dal motore (coppia di spunto in rapporto a quella massima, coppia rispetto all’inerzia). La seconda soluzione può dare una variazione di velocità, ma non da un controllo in tempo reale, e l’implementazione è valida solo in stato di regime. Questo comporta rischi di sovracorrenti e surriscaldamento, che richiedono un sovradimensionamento del sistema.
La velocità di calcolo dei DSP controller, come il TMS320F240, ed un modello accurato del motore asincrono, hanno consentito lo sviluppo di pilotaggi molto affidabili con controllo di velocità molto accurato.
L’applicazione del controllo vettoriale ad orientamento di campo (Field Oriented Control) ai motori ad induzione, dà un controllo istantaneo ad alte prestazioni (breve tempo di risposta, giusto dimensionamento del motore e dei componenti di potenza).
Questo da alla macchina asincrona molti vantaggi, in un ampio campo d’applicazioni (domestiche, industriali, autotrazione). I vantaggi sono dati dalla natura robusta del controllo, dalla sua realizzabilità ed efficienza, dal costo, dall’elevata coppia di spunto, dalla possibilità d’avere variazioni di velocità in un campo molto elevato, dal controllo diretto della coppia e del flusso e da un’eccellente dinamica.
La tecnologia DSP permette di raggiungere un alto livello di prestazioni ed una riduzione di costi del sistema. Il prezzo ridotto, permette grandi applicazioni; per esempio l’LC2402 della Texas Instruments che ha una potenza di calcolo di 30 MIPS, costa 2,95$ in 10.000 esemplari. Un semplice tool suite per comporre e sviluppare il codice, e delle schede di valutazione, riducono tempo e costo d’installazione.
Da un’analisi di mercato si vede che la maggior parte delle applicazioni industriali di motori, fanno uso del tipo a corrente alternata ad induzione.
Questo è dovuto al fatto che questi motori sono molto robusti, sono affidabili, hanno un basso costo ed un’alta efficienza (fino a 80%). In ogni modo, l'uso di motori ad induzione ha i suoi svantaggi: essi sono difficilmente controllabili, per la complessità del modello matematico che li descrive, che non è lineare durante la saturazione ed i parametri elettrici dipendono dalla temperatura.
Tradizionalmente il controllo dei motori è stato fatto con componenti analogici; essi facilitano il progetto, che è relativamente semplice, e gli elementi sono poco costosi.
Comunque, ci sono molti inconvenienti con i sistemi analogici. L’invecchiamento e la temperatura possono portare delle variazioni al componente che fanno sì che il sistema abbia bisogno di continue regolazioni; all’aumentare dei componenti, l'affidabilità del sistema decresce. I componenti analogici hanno tolleranze maggiori che rendono difficile un progetto preciso.
I sistemi digitali offrono miglioramenti rispetto a quelli analogici. Il movimento è eliminato dalla maggior parte delle funzioni, che sono compiute digitalmente, e possono essere eseguite facilmente tramite software, ed il numero di componenti diminuisce perché molte funzioni sono eseguite su un unico chip
I processori DSP nel futuro avranno sempre una maggiore velocità, alta risoluzione ed utilizzeranno algoritmi senza sensori in modo da ridurre il costo del sistema. Daranno un controllo più preciso in modo da avere un maggiore rendimento e delle basse emissioni d’onde elettromagnetiche. Di solito maggiori prestazioni implicano più calcoli, ma l’uso d’istruzioni moltiplicazione ∓mp; somma ad un ciclo incluse in un DSP aumenta la velocità dei calcoli.
Generalmente l’aritmetica a virgola fissa da migliori prestazioni nel controllo dei motori per due ragioni. In primo luogo, i DSP a virgola fissa costano molto meno di quelli a virgola mobile. In secondo luogo, per la maggior parte delle applicazioni, un range dinamico di 16 bit è sufficiente; quando e se sarà necessario, può essere incrementato implementando i calcoli a virgola mobile tramite software.
Le prestazioni di un motore AC ad induzione dipendono molto dal controllo.
Un microprocessore potente come un DSP controller fa le seguenti operazioni:

Per controlli avanzati, possono eseguire anche:
Le applicazioni saranno sviluppate in quei settori in cui i già menzionati vantaggi rispondono alle esigenze dei clienti.
Tipiche applicazioni possono essere:
Come il primo DSP ottimizzato per il controllo digitale dei motori, il TMS320C24x è un unico chip, basato su un DSP centrale con aritmetica a virgola fissa, con una potenza di calcolo di 20 MIPS, circondato da alcuni micro-controllori come ad esempio memoria, modulatori d’impulsi (PWM), convertitori analogico-digitale, e consente il controllo digitale dei motori.
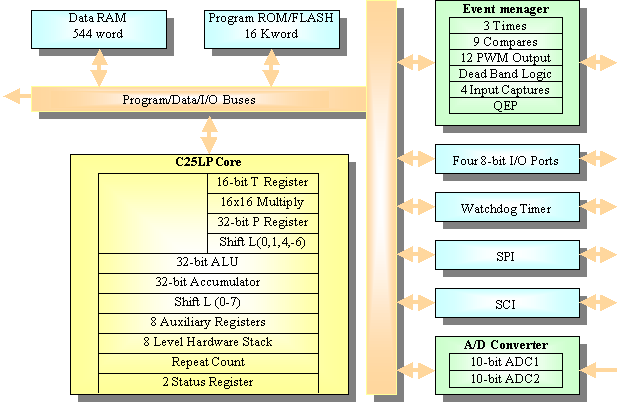
Un modulo di comando dedicato, genera l’uscita e acquisisce i segnali d’ingresso con un minimo carico della CPU. Sono disponibili fino a 4 ingressi e 12 uscite PWM. Tre tempi base possono essere usati per generare segnali d’uscita, che possono essere totalmente indipendenti, sincronizzati, o ritardati fra loro. Ciascun tempo basa ha 6 modi diversi e supporta quello simmetrico e quello asimmetrico. A seconda del tempo base usato, la precisione dell’uscita può arrivare fino a 50 ns. Possono essere generate tre coppie di segnali PWM, usando una dead-band programmabile da 50 ns a 102 ms. Queste tre coppie possono essere comandate dalla SVM, un metodo per pilotare i convertitori trifase.
L'apparecchiatura include un watchdog timer ed un modulo di Real Time Interrupt (RTI).
Il modulo watchdog esamina le operazioni software ed hardware. Un interfaccia seriale di comunicazione a tre pin (SCI) permette le comunicazioni tra la CPU e le altre unità periferiche asincrone. C’è anche un’interfaccia seriale periferica ad alta velocità disponibile per le comunicazione tra la CPU e le unità periferiche esterne o altri micro-controllori. Ci sono a disposizione fino a 28 pin di I/O individualmente programmabili.
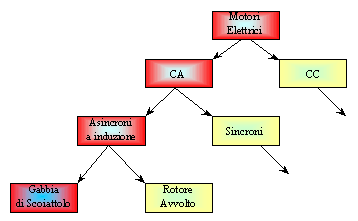
Fra tutti i motori esistenti sul mercato ci sono tre classi principali: il motore a corrente continua, e due diversi motori a corrente alternata, quello sincrono e quello asincrono. Questi motori, quando propriamente controllati, producono una coppia istantanea costante (piccolo ripple di coppia).
Il motore presentato, fa parte di quelli alimentati con tensione alternata. Esso è il motore asincrono a gabbia di scoiattolo, che è anche chiamato motore ad induzione.
La macchina asincrona è una macchina rotante la cui velocità non è rigidamente legata a quella del campo magnetico rotante (velocità di sincronismo) esistente entro la macchina. E’ per questo fatto, cioè appunto perché la velocità di rotazione risulta differente da quella di sincronismo che tale tipo di macchina è stata denominata asincrona. Ma la macchina è chiamata anche ad induzione, non tanto perché pure qui il fenomeno dell’induzione elettromagnetica sia fondamentale (del resto tutte le macchine funzionano sfruttando tale fenomeno) quanto perché la parte rotante è sede esclusivamente di correnti indotte indispensabili per il funzionamento.
L’impiego principale di questa macchina, la quale risulta perfettamente reversibile, è quello come motore.
E’ costituita da una parte fissa e da una parte rotante; la parte fissa detta statore, è formata da un pacco di lamierini Fe-Si aventi la forma di corona circolare. Questa porta all’interno delle cave nelle quali trovano posto i conduttori costituenti l’avvolgimento di statore.
La parte rotante, detta per l’appunto rotore, è interna allo statore e consiste in una struttura cilindrica, costituita anch’essa da un pacco di lamierini in Fe-Si, all’interno del quale passa l’albero di rotazione e nella cui parte esterna, è disposto un certo numero di cave ove trovano posto i conduttori costituenti l’avvolgimento di rotore. L’avvolgimento più diffuso è quello in corto circuito detto a gabbia di scoiattolo.
Il funzionamento si basa sul fatto che il campo magnetico rotante, generato entro la macchina dalla terna di correnti circolanti negli avvolgimenti di statore, determina per induzione una coppia motrice sulla parte mobile. Tale campo magnetico, farà un giro completo nel tempo in cui si compie un’alternanza completa (periodo) della corrente d’alimentazione (ωe).
Ora il rotore, sarà sottoposto all’azione del campo magnetico rotante e diverrà perciò sede di correnti indotte, le quali tendono a metterlo in movimento, e ruoterà ad una velocità che consentirà alle correnti indotte di sviluppare la coppia sufficiente per mantenerlo in rotazione. Però la sua velocità (ωr) non potrà mai raggiungere quella del campo magnetico, perché in tale caso verrebbe meno il moto relativo fra campo magnetico rotante e sistema indotto e non potrebbero svilupparsi le correnti indotte alla cui esistenza è dovuto il movimento.
La differenza tra la frequenza del rotore e quella dello statore è chiamata frequenza di scorrimento (ωslip=ωe- ωr)


Ci sono molti modi per controllare un motore ad induzione in coppia, velocità o posizione; essi possono essere suddivisi in due gruppi: il controllo scalare e quello vettoriale.
Il controllo scalare richiede che le variabili siano controllate solo in ampiezza ed il segnale di retroazione sia proporzionale a quantità continue (cc). Con questo metodo si può solo guidare la frequenza dello statore usando una corrente o una tensione come comando.
Il controllo avviene variando la tensione nello statore in proporzione alla frequenza per mantenere la coppia costante.
Le curve coppia - velocità sono ottenute semplicemente da una traslazione della curva (V0,f0) lungo l’asse delle frequenze mantenendo la forma della curva invariata. Questo metodo ipotizza che le caratteristiche del motore siano stabilizzate (transitorio esaurito) ed assume che la tensione e la corrente dello statore siano sinusoidali.
I vantaggi di questa tecnica sono la sua semplicità: è facile e veloce da programmare e richiede solo poche capacità del calcolo.
Gl'inconvenienti sono un tempo di reazione non buono per cambi del carico e l'efficienza durante questi punti dell'operazione.
Nel controllo vettoriale si fa riferimento non solo alla dimensione, ma anche alla fase delle variabili. Matrici e vettori sono usati per rappresentare le quantità del controllo.
Questo metodo prende in considerazione, non solo Le condizioni di regime, ma vere equazioni matematiche che descrivono il motore, il controllo ottenuto ha una migliore dinamica per variazioni della coppia in un campo di velocità più ampio. La teoria dei fasori permette di maneggiare le equazioni.
Sebbene i motori ad induzione abbiano una struttura molto semplice, il modello matematico è reso complesso dall'accoppiamento tra un gran numero di variabili e dalle non linearità. Il Controllo del Campo Orientato (FOC), offre una soluzione per aggirare il bisogno risolvere equazioni d’ordine elevato, e raggiunge un controllo efficiente con un’alta dinamica.
Quest’approccio, ha bisogno di più calcoli che uno schema standard V/f, ma può essere risolto dall'uso di un'unità del calcolo che includa un DSP; ed ha i seguenti vantaggi:
Il FOC consiste nel controllare le correnti dello statore rappresentate da un vettore. Questo controllo è basato su delle proiezioni che trasformano un sistema trifase dipendente dal tempo e dalla velocità in un sistema a due coordinate (d,q) indipendenti dal tempo.
Queste proiezioni rendono la struttura simile ad una macchina a corrente continua. Le macchine controllate con quest’algoritmo richiedono in ingresso due costanti come riferimento:
Il FOC è basato sulla proiezione della struttura di controllo che non richiede valori istantanei delle quantità elettriche in gioco.
Questo rende il controllo accurato in ogni situazione di lavoro (regime e transitorio) ed è indipendente dai limiti di validità del modello matematico.
Il FOC risolve il classico problema di controllo con i seguenti vantaggi:
Mantenendo l’ampiezza del flusso del rotore (ΨR) ad un valore fisso, abbiamo una relazione lineare tra la coppia e la componente di coppia (isq). Possiamo dunque controllare la coppia del motore tramite la componente di coppia del vettore della corrente statorica.
La tensione, la corrente ed il flusso trifase di un motore AC possono essere analizzata in termini vettoriali in uno spazio complesso.
Per quanto riguarda le correnti, lo spazio vettoriale può essere così definito: siano ia, ib, ic le correnti istantanee nelle fasi dello statore; allora il vettore complesso che rappresenta la corrente statorica is è definito da:
dove α= ej2/3π e α2= ej4/3π, rappresentano gli operatori spaziali.
Il grafico seguente mostra lo spazio vettoriale complesso delle correnti statoriche:

Dove (a,b,c) sono gli assi del sistema trifase.
Questa trasformazione può essere ottenuta in due passi:
Lo spazio vettoriale può essere riportato in un altro sistema di riferimento con solo due assi ortogonali (α,β).
Assumendo che gli assi a ed α abbiano la stessa direzione:

La trasformazione che ci permette di fare questo è:
 Sistema equilibrato: ia + ib + ic = 0
Sistema equilibrato: ia + ib + ic = 0
Abbiamo ottenuto un sistema di riferimento che dipende dal tempo e dalla velocità.
Questa è la trasformazione più importante nel FOC, infatti ci permette di passare ad un sistema di riferimento (d,q) rotante.
Se consideriamo l’asse d allineato al flusso, la figura successiva mostra, per il vettore corrente, la relazione esistente fra i due sistemi di riferimento:

dove θ è la posizione del flusso
Le componenti, di flusso e di coppia del vettore is sono determinate da:
Queste nuove componenti dipendono dalle componenti del vettore della corrente in (α,β) e dalla posizione del flusso del rotore.
Se noi conosciamo l’esatta posizione del flusso, le componenti (d,q) diventano costanti.
Otteniamo un sistema con le seguenti caratteristiche:
Per quanto riguarda la trasformazione delle tensioni, introduciamo solo l’equazione che modifica le tensioni dal sistema di riferimento rotante al sistema ortogonale (α,β)
All’uscita di questo blocco ho le componenti del vettore di riferimento che chiameremo Vr; esso è il vettore (nello spazio) di tensione che sarà applicato al motore.
La seguente figura mostra uno schema base per il controllo della coppia con il FOC.

Si misurano le correnti di due fasi del motore; queste entrano nel modulo che fa la trasformazione di Clarke, e quindi in quello che fa la trasformazione di Park.
Le componenti isq ed isd, sono comparate con i rispettivi valori di riferimento.
A questo punto la struttura di controllo mostra un interessante vantaggio: essa può essere utilizzata sia per il pilotaggio di motori sincroni che ad induzione, semplicemente cambiando il flusso di riferimento ed ottenendo la posizione del flusso.
Nei motori sincroni a magnete permanente il flusso è fisso (determinato dai magneti) e non c’è necessità di crearlo, quindi, quando controlliamo questo tipo di motori (PMSM) isdref deve essere posta a zero.
Invece nei motori ad induzione, il flusso deve essere creato, quindi isdref non può essere nulla.
Questo risolve un inconveniente delle strutture di controllo “classiche”: la portabilità da pilotaggi di macchine asincrone a pilotaggi di macchine sincrone.
Il comando di coppia isdref può essere l’uscita del regolatore di velocità.
Le uscite dei regolatori di correnti sono Vsdref e Vsqref; esse passano attraverso il blocco che fa la trasformazione inversa di Park ottenendo le componenti del vettore di tensione dello statore nel sistema di riferimento stazionario ortogonale (α,β). Questi sono gli ingressi del modulatore ad impulsi PWM che pilota l’inverter.
E’ necessario conoscere le correnti di due fasi (se il motore è connesso a stella, la corrente della terza fase è anche nota dalla relazione ia+ib+ic=0), e la posizione del flusso del rotore.
La misura delle correnti di fase ia e ib, è campionata e convertita da un convertitore A/D.
Il corretto funzionamento del FOC dipende molto dalla bontà delle misurazioni.
La conoscenza della posizione del flusso del rotore è il nocciolo del FOC. Infatti, se c’è un errore in questa variabile, il flusso non è allineato all’asse d ed isd e isq non sono più le componenti esatte della corrente del rotore.
La figura seguente mostra, nei sistemi di riferimento (a,b,c), (α,β) e (d,q) la posizione corretta del flusso, la corrente ed il vettore di tensione dello statore che ruota assieme a (d,q) alla velocità di sincronismo.

La misura della posizione del flusso è differente a seconda che consideriamo una macchina sincrona o ad induzione.
Questo modulo ha in ingresso le due correnti isd e isqe la velocità del rotore. Il modello consiste nell’implementare due equazioni del motore nel sistema di riferimento (d,q)
Dove θ è la posizione del flusso, imR è la corrente di magnetizzazione e dove indicando con LR ed RR rispettivamente l'induttanza e la resistenza del rotore
è la costante di tempo del rotore (ωb è la velocità angolare nominale). La conoscenza di questa costante è critica per il corretto funzionamento del modello.
Assumendo che isqk+1≈ isqk le equazioni possono essere così discretizzate:
Abbiamo così calcolato la velocità del flusso (fS); la posizione del flusso (θcm) è calcolata con la seguente formula d’integrazione:
La posizione del flusso appartiene all’intervallo [0,2Π]. Per dare una buona risoluzione sono utilizzati interi a 16 bit. Possiamo ora vedere la relazione fra la posizione del flusso e la sua rappresentazione numerica:

In conclusione, il modello della corrente è un blocco con in ingresso le variabili isd, isq, n ed in uscita la posizione del flusso θcm.

Grazie al FOC è possibile controllare, direttamente e separatamente, la coppia ed il flusso di una macchina a corrente alternata.
Le macchine controllate con quest’algoritmo, hanno tutti i vantaggi dei motori a corrente continua: controllo istantaneo delle quantità separate che permette una gestione accurata sia del transitorio sia dello stato di regime.
Oltre a questo, esse risolvono i problemi meccanici di commutazione che possiedono le macchine a corrente continua.
Come già detto, il sistema utilizza due costanti come parametri di controllo: la componente di coppia di riferimento (Isqref) e la componente di flusso di riferimento (Isdref).
Il classico regolatore numerico PI (proporzionale e integrale) è posto per regolare la linea di ritorno della coppia e del flusso ai valori desiderati con una scelta corretta del termine P (Kpi) e del termine I (Ki) che sono responsabili rispettivamente dell’errore di sensibilità e dell’errore a regime.
L’espressione numerica del regolatore PI è:
che può essere così rappresentato:

Durante il normale funzionamento, possono esserci grandi variazioni dei valori di riferimento, o ci possono essere grandi disturbi che possono causare la saturazione e l’overflow delle variabili e dell’uscita. Se non controllate, questo tipo di non linearità, danneggiano le prestazioni dinamiche del sistema.
Per risolvere questo problema, una soluzione è di aggiungere una correzione all’integratore come mostrato nella figura seguente:

L’algoritmo di correzione del termine integrale in un linguaggio ad alto livello è:

Dove umax e umin sono dei limiti per le variabili d’uscita.
La struttura di un tipico inverter trifase è mostrata in figura 13. Va, Vb e Vc sono le tensioni applicate alle fasi del motore. Q1Q6 sono sei transistor di potenza che formano l’uscita, i quali sono controllati da a, a’, b, b’, c, c’. Per pilotare motori ad induzione a corrente alternata, quando i transistor superiori sono in saturazione, cioè quando a, b o c sono posti ad 1, il corrispondente transistor inferiore dovrà essere interdetto ossia a’, b’ o c’ saranno posti a 0. Gli stati d’interdizione, saturazione dei transistor superiori, o equivalentemente lo stato di a, b, c sono sufficienti per dare la tensione d’uscita.

La relazione esistente tra il vettore delle variabili di commutazione [a b c] t, ed il vettore delle tensioni di linea (o concatenate) [Vab Vbc Vca] t, è data da:
 (13)
(13)
da questa ricaviamo le equazioni che danno il vettore delle tensioni di fase (o stellate) [Va Vb Vc] t, dove Vdc è la tensione continua che alimenta l’inverter.
 (14)
(14)
Come si vede nella figura 13, ci sono otto possibili combinazioni. Osserviamo che gli stati dei transistor di sotto sono opposti allo stato del rispettivo transistor soprastante, e sono completamente determinati una volta noti quelli di sopra. Le otto combinazioni e le relative tensioni sono riportate nella tabella:
| a | b | c | Va | Vb | Vc | Vab | Vbc | Vca |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 0 | 2/3 | -1/3 | -1/3 | 1 | 0 | -1 |
| 0 | 1 | 0 | -1/3 | 2/3 | -1/3 | -1 | 1 | 0 |
| 1 | 1 | 0 | 1/3 | 1/3 | -2/3 | 0 | 1 | -1 |
| 0 | 0 | 1 | -1/3 | -1/3 | 2/3 | 0 | -1 | 1 |
| 1 | 0 | 1 | 1/3 | -2/3 | 1/3 | 1 | -1 | 0 |
| 0 | 1 | 1 | -2/3 | 1/3 | 1/3 | -1 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
In questo modo si genera un’uscita con una minore distorsione armonica delle tensioni o correnti applicate alle fasi del motore, ed è un modo più efficiente d'usare un alimentatore, rispetto alla modulazione sinusoidale.
Il risultato di ciò, sono sei vettori diversi da zero e due nulli. I vettori diversi da zero sono disposti sugli assi di un esagono, come mostrato in figura 14, e l’angolo fra due consecutivi è di 60°. I vettori nulli sono nell’origine ed applicano una tensione nulla al motore. Gli otto vettori sono chiamati base dello spazio e sono indicati da U0, U60, U120, U180, U240, U300, O000 e O111.
L'obiettivo è di approssimare la tensione di riferimento Vref con una combinazione degli otto vettori. Un metodo semplice è affermare che la media dell’uscita dell’inverter (in un periodo T, piccolo) sia la stessa di Vref nello stesso periodo. Come si può vedere dall’equazione (15), dove T1 e T2 sono rispettivamente la durata in tempo di Ux e Ux±60, i quali delimitano il settore in cui è contenuto il vettore di riferimento.
Assumendo che il periodo Tpwm del PWM sia piccolo, e che le variazioni di Vref siano relativamente lente, dall’equazione (15) otteniamo la (16).

La tensione d’uscita voluta Vref può essere approssimata applicando il vettore Ux per un tempo T1, ed il vettore Ux+60 (Ux-60) per un tempo T2. Se la somma di T1 e T2 è minore o uguale a TPWM, il vettore nullo (000 o 111) dovrà essere inserito per il resto del periodo. Perciò l’equazione (16) diventa:
dove T1+T2+T0=TPWM.
Poiché la tensione che si vuole generare è una sinusoide trifase con uno sfasamento di 120°, Vref è un vettore rotante attorno all’origine del piano (α,β) con la frequenza della tensione trifase voluta. Quindi l’ampiezza di Vrefè limitata dalla circonferenza inscritta nell’esagono, di conseguenza il modulo massimo dell’uscita sarà Vdc/√2; di conseguenza il massimo valore efficace delle tensioni di linea e delle tensioni di fase saranno rispettivamente Vdc/√2 e Vdc/√3, che sono 2/√3 volte maggiori, rispetto alle tensioni che si genererebbero con delle sinusoidi.
Un esempio è mostrato in figura 15.

Le forme d’onda sono simmetriche rispetto alla metà del periodo TPWM.
Lo SVPWM genera una minima distorsione armonica della corrente. Esso garantisce un uso più efficiente del generatore di tensione rispetto alla modulazione sinusoidale;
infatti, nella modulazione sinusoidale convenzionale, il segnale è comparato ad un’onda triangolare, e il luogo in cui sta il vettore di riferimento, è un cerchio di raggio Vdc/2. Nella modulazione SV, la lunghezza d’ogni vettore della base è 2Vdc/3.
A regime l’ampiezza del vettore di riferimento deve essere costante; questo implica che il luogo in cui può variare questo vettore sarà il cerchio inscritto nell’esagono, che ha un raggio di Vdc/√3.

La massima tensione d’uscita generata con la SV, è 2/√3 volte maggiore dell’uscita che si otterrebbe con una modulazione sinusoidale convenzionale.
In certe circostanze, è possibile estendere il campo di velocità oltre quella nominale.
Mostreremo come sia possibile raggiungere velocità superiori a quattro volte quella nominale, sotto certe condizioni. Al di sotto del carico nominale, la potenza meccanica è una funzione lineare della velocità, fino al valore nominale. In questo campo operativo il flusso è mantenuto costante e uguale a φ0.
Assumendo che la potenza meccanica sia proporzionale alla coppia ed alla velocità e che il suo valore nominale sia raggiunto quando la velocità è quella nominale, la coppia prodotta deve essere ridotta se si supera questo valore.

Ci sono tre differenti zone; nella regione a potenza costante, la coppia nominale si comporta come l’inverso della velocità, in tal modo la potenza rimane costante (P=M·ω).
Nella regione in cui è costante il prodotto potenza velocità, la coppia nominale prodotta si comporta come l’inverso del quadrato della velocità.
Le condizioni per avere un campo di velocità esteso, sono principalmente sulle tensioni di fase, e secondariamente sulle correnti di fase.
Assumendo che la tensione di fase cresca con la velocità, e che non possa superare il valore nominale, la componente di flusso, deve essere ridotta in modo da rispettare tale vincolo, e permettere che sia raggiunta la velocità desiderata.
Sappiamo che le correnti di fase aumentano con il carico; la massima coppia resistente nel campo di velocità esteso deve essere tale da mantenere le suddette correnti al di sotto del loro valore nominale; quindi la massima coppia resistente decresce all’aumentare della velocità.

Notiamo che i vincoli sulle tensioni e correnti devono essere rispettati a regime, infatti durante i transitori, la corrente può superare di diverse volte il suo valore massimo senza nessun rischio, poiché il conseguente surriscaldamento, può essere dissipato prima di compiere un’altra operazione di transizione.
L'effetto d’indebolimento del campo essere raggiunto con un avanzamento del vettore della corrente oltre δ=π/2, questo mezzo introduce una componente di corrente nel semiasse negativo d; come conseguenza, isq e la coppia, sono ridotte in modo da non superare la massima corrente d’uscita is_max:
Ci sono due modi possibili per effettuare un'operazione d’indebolimento del campo.
Il più semplice è un controllo a ciclo aperto per l’asse d della corrente. Nonostante la relativa semplicità di realizzazione, ha i seguenti inconvenienti:
Un controllo a ciclo chiuso evita questi tre effetti negativi. Esso consiste nel portare all’ingresso con un regolatore proporzionale e integrale (PI) le componenti lungo gli assi d e q delle tensioni applicate al motore e nel calcolare un nuovo valore di riferimento per la corrente di magnetizzazione. Questo metodo permette di sfruttare a pieno la tensione dell’inverter.
Nel caso di una variazione dell'alimentazione, la tensione sulla fase d’ingresso nel motore deve rimanere costante. La tensione del bus a corrente continua dell’inverter, è usata come reazione, di un loop di controllo, contenente un regolatore proporzionale. Questa soluzione permette di usare il motore come un freno senza il bisogno d’avere una resistenza che dissipi potenza.
Per mezzo della tensione di controllo si può utilizzare il motore per dissipare energia. In questo caso, il controllo regola la massima coppia frenante possibile in modo che la tensione, del bus in corrente continua, non superi il valore massimo ammissibile.


Nella maggior parte degli inverter è richiesta un’informazione sulla fase della corrente. Il primo metodo per ottenerla, è di misurarla direttamente, ma questo richiede, a seconda dello schema del carico, almeno due sensori applicati direttamente sulle fasi del motore. Questi tipi di sensori, di solito, sono costosi perché devono essere isolati e perciò sono sofisticati.
L'altra via consiste nel misurare solo la corrente di linea, e stimare le tre correnti di fase.
Questo metodo richiede un semplice SHUNT come sensore.

Come controlliamo direttamente gli stati di commutazione dell’inverter, si può conoscere l'esatta strada che percorre la corrente dall’ingresso dell’inverter alla fase del motore. Possiamo allora determinare il collegamento della fase alla linea della corrente continua. L'informazione che otteniamo sulla corrente di fase è il risultato di una misura reale, e non il risultato di una simulazione che richiede un modello del circuito d’uscita. Il processo della misurazione è totalmente indipendente da cosa è collegato all’ingresso e all’uscita dell’inverter.
La figura seguente dà un esempio di uno stato di commutazione.

Con riferimento a quanto precedentemente descritto, consideriamo lo stato di commutazione (a,b,c)=(0,0,1), la corrente di una fase (ic), può essere messa in relazione con la corrente continua. Perciò posso misurare le correnti delle tre fasi, guardando solamente la linea a corrente continua. Se il periodo del modulatore PWM, è abbastanza elevato, la corrente di fase varia solo leggermente in uno o due periodi.
Quindi, la misura passata della corrente di una fase dà un’approssimazione ragionevole della corrente attuale.
Per ottenere le correnti delle tre fasi il DSP necessita di un solo canale A/D e di alcuni calcoli; rispetto al metodo classico che richiederebbe due o tre canali A/D e l’uso di sensori costosi.
La via più comune per misurare la velocità del motore sull'asta, è l'uso di un codificatore incrementale o di un generatore tachimetrico.
Nel caso di un codificatore, il TMS320C240 include un modulo (Q.E.P.) che gestisce perfettamente la situazione, e calcola la velocità e la direzione della rotazione usando solo due entrate digitali ed un registro interno a 16 o 32 bit.
Ci sono molti tipi di generatori tachimetrici, alcuni danno una tensione continua proporzionale alla velocità del motore, altri generano un determinato numero d’impulsi per ogni giro del rotore.
Nel primo caso uno dei 16 canali del convertitore A/D del TMS320C240 è collegato all’uscita del generatore tachimetrico.
Gli impulsi entrano in un modulo che ne misura la frequenza. L’implementazione software avviene ad intervalli fissi, non superiori al periodo della minima frequenza misurabile.
Siccome c’è solo un segnale, non è possibile conoscere il senso di rotazione; si usa un artificio per aggiungere il segno alla misura della velocità. Il segno è memorizzato in una variabile e solo quando il motore scende sotto un determinato numero di giri, questa variabile è aggiornata con il segno corrente. Questo permette, anche d'eseguire veloci inversioni del senso di rotazione del motore.
In molti casi è impossibile usare sensori di velocità o rilevatori di posizione perché è tecnicamente impossibile, o è troppo costoso. Fra i sistemi capaci di controllare la velocità di un motore ad induzione, senza sensori, c’è l’osservatore KALMAN. Esso ha un buon comportamento dinamico, e un’elevata resistenza ai disturbi. Con il controllo ad orientamento di campo, le variabili necessarie: posizione, velocità e flusso del rotore, sono stimate con un osservatore di Kalman.
Implementare un osservatore è un problema molto complesso, e richiede il modello del motore ad induzione. Le equazioni dell’osservatore sono calcolate di solito tramite moltiplicazioni matriciali ed un’inversione di matrice.
Questi calcoli richiedono un processore ad alte prestazioni per essere eseguiti in tempo reale. I DSP sono particolarmente adattati per questo scopo, a causa del suo buon rapporto prestazioni/prezzo.
Il sistema è descrivibile con le seguenti equazioni:
 (19)
(19)
dove r e ρ sono rispettivamente i disturbi del sistema e delle misurazioni. La prossima ipotesi riguarda il rumore: supponiamo sia stazionario, bianco, incorrelato e Gaussiano, e con media nulla.
Sotto, è riportato un esempio d’implementazione e realizzazione di un controllo di velocità di un motore asincrono collegato ad un generatore di tensione alternativo.

Il filtro d’ingresso contiene anche le protezioni hardware, un filtro EMI ed un opzionale correttore del fattore di potenza (PFC). Il PFC può essere attivo o passivo; nel caso attivo, può essere maneggiato interamente dal DSP. Per ottenere una tensione continua dall’ingresso alternativo, su usa un ponte di diodi con un condensatore, rappresentato dal blocco rettificatore. Per generare le tensioni di fase con ampiezza e frequenza variabili, si usa un inverter trifase, basato su tecnologia IGBT. Il sistema è controllato dal DSP TMS320C240. Le entrate sono: un generatore tachimetrico, che misurare la velocità; un partitore resistivo, per misurare la tensione del bus a corrente continua (VBUS); un sensore resistivo sulla linea (IBUS), per valutare le correnti di fase; ed un sensore della temperatura. Il controllore usa una porta seriale per il collegamento esterno. Il generatore ausiliare alimenta i circuiti logici.

Il controllo usa un modulatore PWM con controllo vettoriale ad orientamento di campo. È utilizzato uno schema a ciclo chiuso per raggiungere alte velocità.
Il controllo di tensione del bus a corrente continua, ha una limitazione per iq per poter utilizzare il motore come freno, mantenendo la tensione sotto il limite massimo.
Il controllo della velocità, del flusso e delle correnti, sono implementati utilizzando regolatori PI standard, con doppia precisione per la parte integrale. C’è anche una protezione contro le alte temperature
Lo schema di controllo proposto è implementato sul TMS320C240 della Texas Instruments. Tutte le routine di controllo sono state fatte usando un linguaggio assembler con una rappresentazione numerica a virgola fissa.
L’algoritmo di controllo è sincronizzato dal timer interno al DSP che genera gli interrupts.
La velocità è controllata una volta ogni molti cicli tramite un generatore tachimetrico.
La misura della corrente delle fasi richiede un campionamento della corrente continua dell’inverter durante il periodo del PWM (che è di 16 kHz). Il tempo di campionamento varia con una funzione che dipende dal pattern attuale del PWM. Questo è ottenuto pilotando la conversione A/D attraverso un altro interrupt (Compare Register interrupt).
La memoria necessaria è minore di 3K word di ROM, e 544 word di RAM, ed uso meno del 50% (10 MIPS) della potenza di calcolo del DSP. Tutto il ciclo di controllo è calcolato in meno di 35 μs.
La velocità varia da 0 a 12.000 giri al minuto con un errore massimo al disotto del 1%.
L’efficienza della potenza elettrica è dell’ordine del 95%, e l’efficienza totale del sistema è maggiore del 85%.
Questa è una panoramica su una nuova tecnica di controllo. Il DSP-Controller TMS320C240 combina le prestazioni di un DSP, con l’architettura periferica ottimizzata di un Microcontroller in un unico chip per il controllo di un motore ad induzione.
Col DSP controller si fa un approccio intelligente al controllo, in modo da ridurre il costo complessivo del sistema e migliorarne l’affidabilità.