Le porte logiche
(parte seconda)
Le porte logiche esaminate nel numero scorso si dividono in porte logiche fondamentali e porte logiche derivate.
Quelle fondamentali sono: somma logica OR, prodotto logico AND e negazione NOT.
Le porte logiche derivate sono: la somma logica negata NOR, il prodotto logico negato NAND, l’OR esclusivo XOR o circuito di anticoincidenza e il NOR esclusivo XNOR o circuito di coincidenza.
Le porte logiche fondamentali costituiscono i mattoni dell’elettronica digitale.
Con esse è possibile realizzare qualsiasi circuito digitale dal più semplice al più complesso.
È, inoltre, possibile verificare che anche con le sole porte NOR o con le sole porte NAND è possibile realizzare qualsiasi circuito digitale. È sufficiente, infatti, verificare che con le sole porte NAND, ad esempio, si può realizzare il NOT, l’OR e l’AND.
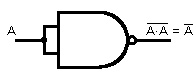
Infatti collegando tra loro gli ingressi A e B della porta NAND come in figura 1 si ottiene il NOT:

Fig.1 - NOT realizzato con una porta NAND.
Per ottenere l’AND è sufficiente far seguire la porta NAND da un NOT realizzato come in figura 1.
Per ottenere l’OR, infine è sufficiente far precedere ciascun ingresso del NAND da un NOT come in fig.2. Infatti, per il noto teorema di De Morgan, la somma logica è il complemento del prodotto dei complementi.
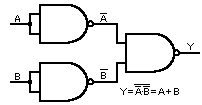
Fig.2 - OR realizzato con porte NAND.
Progettazione di un semplice circuito digitale combinatorio.
Si vuole realizzare un circuito digitale combinatorio con tre ingressi A B C ed una uscita Y.
L’uscita deve valere 1 se almeno due ingressi sono uguali ad 1. Se, invece, vale 1 un solo ingresso o nessuno di essi l’uscita Y deve valere 0 (problema della maggioranza).
Risoluzione
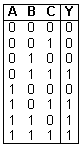
Compiliamo una tabella, nota come tabella della verità, in cui in ciascuna riga applichiamo le possibili combinazioni binarie tra gli ingressi A B C. Tali combinazioni sono: 23=8.
In corrispondenza di ciascuna di esse sarà possibile, grazie alla formulazione del problema, assegnare all’uscita Y il valore 0 o il valore 1.
Dalla tabella osserviamo che l’uscita Y assume il valore 1 in corrispondenza delle combinazioni ABC pari a 011, 101, 110 e 111.
Nell’ultima combinazioni tutti gli ingressi sono a 1 per cui, a maggior ragione, risulta Y=1.
Per le altre combinazioni l’uscita Y vale 0 come richiesto dal problema.
Come si realizza il circuito? Sarà, innanzitutto, necessario ricavare l’espressione algebrica dalla tabella della verità.
Il procedimento è il seguente: si considerano le combinazioni delle variabili di ingresso che rendono l’uscita Y uguale a 1. La combinazione di ingresso da considerare conterrà il prodotto tra A B C e ciascuna variabile sarà considerata in forma naturale o in forma negata a seconda se assume il valore 0 o 1. La prima combinazione che rende l’uscita uguale a 1 è: ABC=011, cioè A=0, B=1 e C=1. Allora A dovrà essere considerata in forma negata (complementata), mentre B e C in forma naturale (cioè senza negazione). I quattro termini che rendono la variabile di uscita Y uguale a 1 devono, poi, essere sommati (somma logica !!) tra di loro.
In definitiva si ottiene:
![]()
Questa espressione si può semplificare algebricamente applicando le regole dell’algebra di Boole che solo parzialmente coincidono con quelle dell’algebra ordinaria.
In particolare, per la semplificazione che si intende effettuare, si applica la regola che aggiungendo quante volte si vuole un termine già esistente in una espressione, il valore dell’espressione non cambia. L’altra regola è che la somma logica tra una variabile e la stessa variabile negata vale 1.
Nel nostro caso aggiungiamo, nella espressione della funzione Y, il termine ABC per altre due volte. In tal caso il primo termine ha BC in comune con ABC, il secondo ha AC in comune con l’altro ABC aggiunto ed infine il terzo termine ha AB in comune con l’ultimo ABC aggiunto.
Attraverso la messa in evidenza si ottiene:
![]()
A + A=1 e così pure B + B = 1 e C + C = 1 , l’espressione si riduce a:
![]()
L’espressione così minimizzata è una somma di prodotti. Il circuito logico da realizzare sarà costituito da tre porte AND a due ingressi e da una porta OR finale a tre ingressi. In fig.3 si mostra il circuito risolutivo.

Fig.3 - Circuito risolutivo.
Per verificarne il funzionamento è sufficiente attribuire alle variabili di ingresso A B C ciascuna delle otto combinazioni mostrate nella precedente tabella ed eseguendo la somma logica tra i tre termini prodotto BC, AC e AB.