Le porte logiche (parte prima)

Premessa

Le principali parti elettroniche dei computer sono costituite da circuiti digitali che, come è noto, elaborano segnali logici basati sullo 0 e sull’1.

I mattoni fondamentali dei circuiti logici sono, appunto, le porte logiche che sono in grado di soddisfare un’algebra particolare, detta algebra binaria, sviluppata dallo scienziato George Boole (1815-1864).

In questo semplice articolo si introdurranno le porte logiche fondamentali in grado di svolgere le operazioni di somma, prodotto e negazione indicate, rispettivamente, con OR (somma logica), AND (prodotto logico) e NOT (negazione o complementazione).

Si descriveranno, inoltre, le porte logiche derivate NOR (OR seguito da un NOT), NAND (AND seguito da un NOT), XOR (noto come OR esclusivo o circuito di anticoincidenza), XNOR (noto come NOR esclusivo o circuito di coincidenza).

Ogni porta logica ha una o più variabili di ingresso ed una sola variabile di uscita. Le variabili di ingresso e di uscita sono di tipo digitale per cui è possibile inserire in una tabella tutte le possibili combinazioni che si possono verificare tra le variabili di ingresso. L’uscita assume il valore 0 oppure il valore 1 in corrispondenza di ciascuna combinazione delle variabile di ingresso in funzione della definizione assegnata.

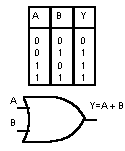
1. Somma logica OR

Si effettua su due o più variabili, l’uscita assume lo stato logico 1 se almeno una variabile di ingresso è allo stato logico 1.

Nel caso di due variabili di ingresso A e B, detta Y la variabile di uscita, si scrive: Y=A+B e si legge A or B.

Nella seguente figura si mostra la tabella della verità con le quattro possibili combinazioni tra A e B ed il simbolo logico relativo ad una porta OR a due ingressi. Nella colonna Y si sono posti i valori assunti dall’uscita Y che soddisfa la definizione della porta OR.

OR

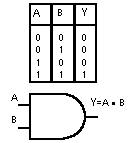
2. Prodotto logico AND

Si effettua su due o più variabili, l’uscita assume lo stato logico 1 solo se tutte variabile di ingresso sono allo stato logico 1.

Nel caso di due variabili di ingresso A e B, detta Y la variabile di uscita, si scrive: Y=A·B e si legge A and B.

Nella seguente figura si mostra la tabella della verità con le quattro possibili combinazioni tra A e B ed il simbolo logico relativo ad una porta AND a due ingressi. Nella colonna Y si sono posti i valori assunti dall’uscita Y che soddisfa la definizione della porta AND.

AND

 

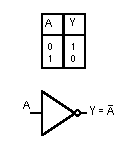
3. Negazione

Si effettua su una sola variabile. L’uscita assume il valore logico opposto a quello applicato in ingresso.

Detta A la variabile di ingresso la negazione si scrive: Y = A e si legge A negato oppure A complementato.

Nella seguente figura si mostra la tabella della verità con le due possibili combinazioni di A ed il simbolo logico relativo ad una porta NOT. Nella colonna Y si sono posti i valori assunti dall’uscita Y che soddisfa la definizione della porta NOT.

NOT

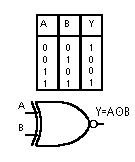
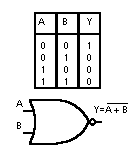
4. Somma logica negata NOR

Si effettua su due o più variabili, l’uscita assume lo stato logico 0 se almeno una variabile di ingresso è allo stato logico 1. In tutti gli altri casi Y=1.

Per due variabili di ingresso A e B:   Y= A+B e si legge A nor B.

Nella seguente figura si mostra la tabella della verità con le quattro possibili combinazioni tra A e B ed il simbolo logico relativo ad una porta NOR a due ingressi. Nella colonna Y si sono posti i valori assunti dall’uscita Y che soddisfa la definizione della porta NOR.

NOR

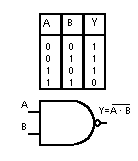
5. Prodotto logico negato NAND

Si effettua su due o più variabili, l’uscita assume lo stato logico 0 se tutte le variabili di ingresso sono allo stato logico 1. In tutti gli altri casi Y=1.

Per due variabili di ingresso A e B: Y = A·B e si legge A nand B.

Nella seguente figura si mostra la tabella della verità con le quattro possibili combinazioni tra A e B ed il simbolo logico relativo ad una porta NAND a due ingressi. Nella colonna Y si sono posti i valori assunti dall’uscita Y che soddisfa la definizione della porta NAND.

NAND

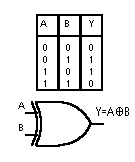
6. OR esclusivo XOR

A differenza delle precedenti porte logiche, l’XOR opera su due soli ingressi. L’uscita vale 1 se gli ingressi assumono valore diverso, vale 0 se gli ingressi sono tra loro uguali. La funzione logica si scrive: e si legge A or esclusivo B oppure A diverso da B.

Nella seguente figura si mostra la tabella della verità con le quattro possibili combinazioni tra A e B ed il simbolo logico relativo ad una porta XOR. Nella colonna Y si sono posti i valori assunti dall’uscita Y che soddisfa la definizione della porta XOR.

XOR

7. NOR esclusivo XNOR

Anche la porta XNOR opera su due soli ingressi. L’uscita vale 1 se gli ingressi assumono valore uguale, vale 0 se gli ingressi sono tra loro diversi. La funzione logica si scrive: e si legge A nor esclusivo B oppure A coincidente con B.

Nella seguente figura si mostra la tabella della verità con le quattro possibili combinazioni tra A e B ed il simbolo logico relativo ad una porta XNOR. Nella colonna Y si sono posti i valori assunti dall’uscita Y che soddisfa la definizione della porta XNOR.

XNOR