
MOTO OSCILLATORIO
Se consideriamo la proiezione P'x sul diametro del cerchio di un punto P che si muove di moto circolare uniforme lungo una circonferenza (Fig. 1), possiamo stabilire che alle diverse posizioni P1, P2, Pn del punto mobile sulla circonferenza in tempi differenti t1, t2, ..tn, corrisponderanno le proiezioni sul diametro AB rispettivamente P'1, P'2, ...P'n.

Fig. 1
Questo tipo di moto Ŕ caratterizzato dall'entitÓ massima dello spostamento rispetto alla posizione di equilibrio, definita ampiezza di oscillazione, e dall'intervallo di tempo che il moto impiega per ripetersi, definito periodo di oscillazione. In stretto rapporto con il periodo (vedi moto circolare) Ŕ la frequenza di oscillazione, definita come il numero di cicli di oscillazione nell'unitÓ di tempo. La frequenza ed il periodo sono l'una l'inverso dell'altra:
![]() (1)
(1)
Dall'anailisi di questo tipo di moto risulta che la velocitÓ ha intensitÓ variabile nel tempo e l'accelerazione Ŕ proporzionale allo spostamento (s); ci˛ dimostra che le variazioni di velocitÓ sono sempre di segno opposto allo spostamento. E' chiaro che la massima accelerazione si ha nei punti A e B (Fig. 1) dove, per un istante, il punto in movimento si arresta prima di invertire il senso del moto e dove la velocitÓ, che cambia di segno, per quell'istante Ŕ nulla.
Indichiamo con s la distanza tra la posizione di un punto proiettato sul diametro ed il centro O e con w la velocitÓ angolare del corrispondente punto situato sulla circonferenza di cui il primo Ŕ la proiezione. Possiamo ora dimostrare mediante l'applicazione della matematica che l'accelerazione istantanea di un moto armonico Ŕ proporzionale alla distanza s:
![]() (2)
(2)
La rappresentazione grafica Ŕ riportata nel diagramma orario di Fig. 2 e corrisponde ad una curva chiamata sinusoide.
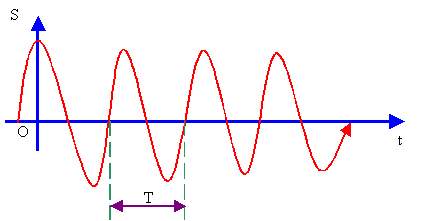
Fig. 2