Moto Circolare Uniforme

    Nel moto circolare la velocità V è costante; eppure si ha un'accelerazione. A che cosa è dovuta?

    Non certo alla variazione della velocità nel tempo, ma alla continua variazione nella direzione  del vettore V (vedi Fig. 1):

Fig. 1

quindi:

(1)

detta accelerazione tangenziale dovuta alla rapidità di variazione della velocità.

    Se leghiamo un corpo di un certo peso ad uno spago e lo facciamo roteare in aria, avremo la sensazione che questo corpo voglia strappare lo spago e "scappare". Questa sensazione reale è data da una forza chiamata Forza centrifuga, cioè forza che "fugge dal centro" e, per la seconda legge della dinamica, ha valore 

F = ma (2)

dove

(3)

ma trattandosi di traiettoria circolare diverrà:

  (4)

    che, per il  terzo principio della dinamica, lo stesso valore è attribuito alla Forza centripeta, cioè forza che "attira verso il centro".

    In questo sistema l'accelerazione a, come mostrato nella (2) non ha valore

(5)

ma bensì

(6)

questo perché l'accelerazione, come visto in premessa, è dovuta alla continua variazione nella direzione  del vettore V.

    Vediamo ora come si dimostra la (6).

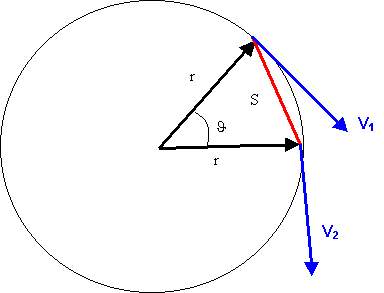
    Con riferimento alla fig. 2, noteremo che il triangolo P₁O P₂ è simile al triangolo composto dal vettore V₁, V₂ e DV.

Fig. 2

    Possiamo quindi trasformare questa similarità in una equazione:

(7)

da cui avremo

(8)

sostituiamo la (8) nella (5) e avremo:

(9)

 sapendo che

(10)

e infine sostituendo la (10) nella (9)

(11)

che altro non è che l'Accelerazione Centripeta (dovuta alla variazione della direzione del vettore V)