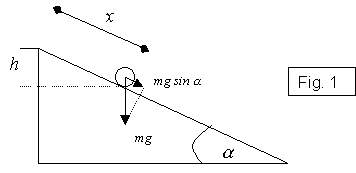
IL PIANO INCLINATO

Con questa tesi si intende dimostrare che una bilia che scende su un piano inclinato arriva a terra allo stesso tempo di una stessa bilia in caduta libera.
Scriviamo la legge di Newton (in equazione) che descrive il moto lungo la guida (escludendo il rotolamento):
![]() (1)
(1)
sappiamo che:
![]() (2)
(2)
integriamo la (2) nella (1):
![]() (3)
(3)
sappiamo anche che:
![]() (4)
(4)
sostituendo la (4) al valore dVx avremo:
![]() (5)
(5)
quindi:
![]() (6)
(6)
questa sarà uguale, trattandosi di piano inclinato a:
![]() (7)
(7)
per cui avremo l’equazione (per la legge di Newton) di:
![]() (8)
(8)
dove m è la massa della bilia e
g è l’accelerazione di gravità, per cui ![]() è la proiezione della forza peso nella direzione parallela alla guida.
è la proiezione della forza peso nella direzione parallela alla guida.
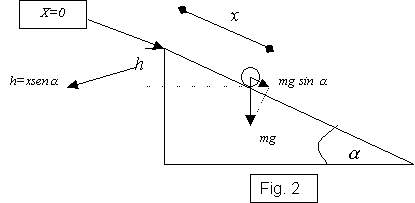
Considerata l’origine dei tempi per x = 0 (come in fig. 2), integrando si hanno velocità e spazio in funzione del tempo:
![]()
quindi:
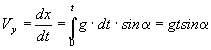 (9)
(9)
ed anche
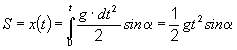 (10)
(10)
dalla (9) avremo che:
![]() (11)
(11)
e dalla (10) avremo invece:
![]() (12)
(12)
quindi elevando al quadrato la (11) risulta che:
![]() (13)
(13)
ed infine l’equazione in funzione del tempo risulta essere:
![]() (14)
(14)
ne risulta che:
![]() (15)
(15)
Con riferimento alla fig. 2 sappiamo che
![]() (18)
(18)
quindi sostituendo la (17) alla (16) avremo:
![]() (19)
(19)
per cui
![]() (20)
(20)
Allo stesso risultato si può giungere subito applicando il principio di conservazione dell’energia:
IN OGNI ISTANTE LA SOMMA DELLE ENERGIE POTENZIALI
E CINETICHE DI UN CORPO E’ COSTANTE
E quindi
Ep=Ec
- ENERGIA POTENZIALE (Ep): è l’energia dipendente dalla quota (h) altimetrica alla quale è posta la massa:
Ep = Forza x spostamento
Dove: F = P (peso della massa unitaria);
s = h (quota altimetrica della massa unitaria)
quindi
Ep = P h = mgh
Ec = Forza x spostamento
Dove: F = massa x aaccellerazione;
Quindi:
![]()
dove
![]() (moto uniformemente accelerato)
(moto uniformemente accelerato)
sostituendo avremo:
![]()
Ma se V = at allora V2 = a2t2 quindi:
![]()
Dalla fisica sappiamo che il peso "P" equivale alla massa "m" per l’accelerazione di gravità "g", quindi tradotto in formula:
![]()
di conseguenza
![]()
sostituendo alla (1) otterremo:
![]()