LEGGI DEI GAS PERFETTI
Per descrivere il comportamento dei fluidi gassosi si assumono equazioni matematiche molto semplici, che legano fra loro tre grandezze:
1) pressione;
2) volume;
3) temperatura.
La loro validità è solo approssimativa e quindi bisogna supporre che i gas si comportino come perfetti (in natura non esistono gas perfetti) trascurando cioè le interazioni tra particelle costituenti e attrito interno.
La prima legge dei gas perfetti riguarda la loro elasticità (relazione fra pressione e volume) a temperatura costante.
Sappiamo che i gas sono più comprimibile dei liquidi. Questa affermazione può essere provata con un esperimento semplice: riempite d'acqua una siringa, tappate il foro d'uscita e premete sullo stantuffo. Noterete che non si notano "compressioni" apparenti. Adesso ripetete l'esperimento riempiendo la siringa con aria anziché con acqua. Noterete che lo stantuffo cala, quindi comprime l'aria. Però man mano che lo stantuffo avanza l'aria opporrà una resistenza sempre maggiore alla compressione. Quale è il motivo?
La LEGGE DI BOYLE MARIOTTE(1) recita che
| IL VOLUME (V) OCCUPATO DA UNA CERTA QUANTITA' DI GAS, A TEMPERATURA COSTANTE, E' INVERSAMENTE PROPORZIONALE ALLA PRESSIONE (p). |
pV = costante
Fra le applicazioni della legge descritta ci sono le bombole di GPL, le bombole di ossigeno dei sub e molti altri.
Adesso vediamo cosa succede all'interno di un'ampolla piena di aria se ne aumentiamo la temperatura, mantenendo la pressione costante.
Poniamo la nostra ampolla in un bagno di acqua. Poniamo all'imboccatura un tappo di sughero con un foro, all'interno del quale infiliamo un tubicino piegato a 90° graduato con una spia (pallina) in posizione "0".
Riscaldiamo l'acqua e osserviamo cosa succede.
Man mano che l'acqua si riscalda, l'aria all'interno dell'ampolla si riscalda a sua volta e causa il movimento della pallina. Ad ogni variazione di temperatura avremo una variazione del volume del gas contenuto nell'ampolla.
Potremo quindi osservare che
| IL VOLUME (V) DEL GAS E' DIRETTAMENTE PROPORZIONALE ALL'AUMENTO DELLA TEMPERATURA QUANDO LA PRESSIONE (p) RIMANE COSTANTE. |
Questa è la Ia LEGGE DI GAY LUSSAC che può essere espressa con la seguente equazione matematica:
DV = Vt - V0 = a V0 (t - t0)
dove Vt è il volume del gas alla temperatura t, V0 il suo volume alla temperatura iniziale t0 e
a il coefficiente di dilatazione cubica (Vt = V0 (1 + at)
Se rappresentiamo in un grafico l'equazione descritta otterremo una retta che interseca l'asse delle ascisse nel punto - 273,16.
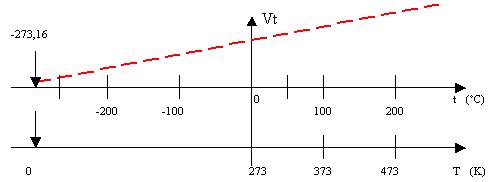
Infatti assumendo t0 = -273,16°C avremo dalla Vt = V0 (1 + at) il seguente risultato
![]()
In pratica significa che se la legge descritta fosse applicabile fino a temperature bassissime, il volume del gas dovrebbe annullarsi per t = -273,16°C (nessun gas si comporta come un gas perfetto fino a tale temperatura).
Il valore di t = -273,16°C corrisponde allo zero assoluto di una scala detta assoluta o scala Kelvin(2)
Adesso proviamo a ripetere l'esperimento descritto sopra con una semplice variante: tappiamo l'ampolla con un tappo di sughero dove abbiamo apposto un manometro. Riscaldiamo l'acqua e osserviamo cosa succede.
Man mano che l'acqua si riscalda, l'aria all'interno dell'ampolla si riscalda a sua volta e causa una pressione maggiore che viene segnalata sul nostro manometro. Ad ogni variazione di temperatura avremo una variazione della pressione nell'ampolla.
Potremo quindi osservare che
| LA PRESSIONE (p) DEL GAS E' DIRETTAMENTE PROPORZIONALE ALL'AUMENTO DELLA TEMPERATURA QUANDO IL VOLUME (V) RIMANE COSTANTE. |
Questa è la IIa LEGGE DI GAY LUSSAC che può essere espressa con la seguente equazione matematica:
Dp = pt - p0 =
b p0 (t - t0)dove pt è la presione del gas alla temperatura t, p0 il suo volume alla temperatura iniziale t0 e
b una costante uguale alla precedente a (coefficiente di dilatazione cubica =quindi per t0 = 0 possiamo scrivere:
pt = p0 (1 + bt)
Se rappresentiamo in un grafico l'equazione descritta otterremo una retta che interseca l'asse delle ascisse nel punto - 273,16.

Infatti assumendo t0 = -273,16°C avremo dalla pt = p0 (1 +
bt) il seguente risultato:![]()
In pratica significa che se la legge descritta fosse applicabile fino a temperature bassissime, la pressione del gas dovrebbe annullarsi per t = -273,16°C (nessun gas si comporta come un gas perfetto fino a tale temperatura).
(1): Stabilita nel 1660 dall'irlandese Boyle e dal francese Mariotte.
(2): Scala inventata dal matematico e fisico britannico William Thomson Kelvin.