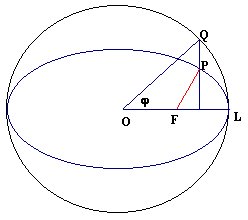

Keplero scoprì che, ovunque fosse il pianeta (P) nella sua orbita, si poteva ottenere in ogni momento la sua distanza dal Sole (F) per mezzo della seguente relazione:
![]()
Ora, questa è la relazione per un punto di una ellisse
avente il Sole in uno dei due fuochi. Il valore e rappresenta l'eccentricità
dell'orbita cioè il rapporto FO/OL.
L'ellisse
è il luogo geometrico dei punti del piano, tali che la somma delle loro
distanze da due punti fissi F' e F'' detti fuochi, è costante, cioè
per qualsiasi punto P che appartiene all'ellisse, la somma delle
lunghezze PF'+PF'' risulta sempre uguale.
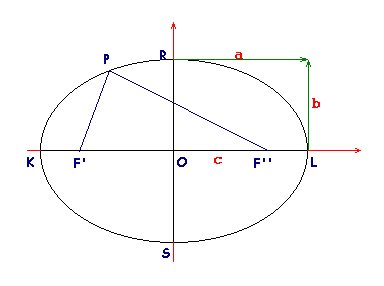
KL è l'asse maggiore, RS l'asse minore. O è il centro dell'ellisse. Se si fissano come assi cartesiani la retta che passa per i fuochi (asse delle x) e la perpendicolare ad essa che passa per il centro (asse delle y), l'equazione dell'ellisse è:
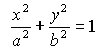
dove a e b sono rispettivamente il semiasse maggiore (OL) e il semiasse minore (OR). Inoltre si ha:
![]()
dove c è la semidistanza focale OF''.
L'eccentricità e di un'ellisse (e=c/a) è un valore minore di 1. Se la semidistanza
focale è nulla (c=0), significa che i
semiassi sono uguali (a=b) e quindi si ottiene una circonferenza
di raggio r=a=b. Maggiore è l'eccentricità (e
si avvicina a 1) tanto più "schiacciata" apparirà la forma
dell'ellisse.
![]()