Galileo Galilei LE MECANICHE Delle utilità che si traggono dalla scienza mecanica e dai suoi instrumenti

ALCUNI AVVERTIMENTI CIRCA LE COSE DETTE

Avendo noi mostrato come i momenti di pesi diseguali vengono pareggiati dall'essere sospesi contrariamente in distanze che abbino la medesima proporzione, non mi pare di doversi passar con silenzio un'altra congruenza e probabilità, dalla quale ci può ragionevolmente essere confermata la medesima verità.

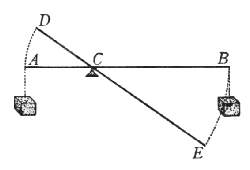
Però che, considerisi la libra AB divisa in parti diseguali nel punto C, ed i pesi, della medesima proporzione che hanno le distanze BC, CA, alternatamente sospesi dalli punti A, B: è già manifesto come l'uno contrapeserà l'altro, e, per consequenza, come, se a uno di essi fusse aggiunto un minimo momento di gravità, si moverebbe al basso inalzando l'altro; sì che, aggiunto insensibile peso al grave B, si moveria la libra, discendendo il punto B verso E, ed ascendendo l'altra estremità A in D. E perché, per fare descendere il peso B, ogni minima gravità accresciutagli è bastante, però, non tenendo noi conto di questo insensibile, non faremo differenza dal potere un peso sostenere un altro al poterlo movere. Ora, considerisi il moto che fa il grave B, discendendo in E, e quello che fa l'altro A, ascendendo in D; e troveremo senza alcun dubbio, tanto esser maggiore lo spazio BE dello spazio AD, quanto la distanza BC è maggiore della CA; formandosi nel centro C due angoli, DCA ed ECB, eguali per essere alla cima, e, per conseguenza, due circonferenze, BE, AD, simili, e aventi tra di sé l'istessa proporzione delli semidiametri BC, CA, dai quali vengono descritte. Viene adunque ad essere la velocità del moto del grave B, discendente, tanto superiore alla velocità dell'altro mobile A, ascendente, quanto la gravità di questo eccede la gravità di quello; né potendo essere alzato il peso A in D, benché lentamente, se l'altro grave B non si muove in E velocemente, non sarà maraviglia, né alieno dalla costituzione naturale, che la velocità del moto del grave B compensi la maggior resistenza del peso A, mentre egli in D pigramente si muove e l'altro in E velocemente descende. E così, all'incontro, posto il grave A nel punto D e l'altro nel punto E, non sarà fuor di ragione che quello possa, calando tardamente in A, alzare velocemente l'altro in B, ristorando, con la sua gravità, quello che per la tardità del moto viene a perdere. E da questo discorso possiamo venire in cognizione, come la velocità del moto sia potente ad accrescere momento nel mobile, secondo quella medesima proporzione con la quale essa velocità di moto viene augumentata.

Un'altra cosa, prima che più oltre si proceda, bisogna che sia considerata; e questa è intorno alle distanze, nelle quali i gravi vengono appesi: per ciò che molto importa il sapere come s'intendano distanze eguali e diseguali, ed in somma in qual maniera devono misurarsi.

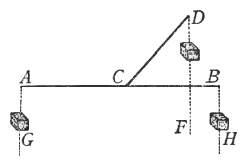
Imperò che, essendo la linea retta AB, e dalli estremi punti di essa pendendo due eguali pesi, preso il punto C nel mezzo di essa linea, si farà sopra di esso l'equilibrio; e questo, per essere la distanza AC eguale alla distanza CB. Ma se, elevando la linea CB e girandola intorno al punto C, sarà trasferita in CD, sì che la libra resti secondo le due linee AC, CD, gli due eguali pesi pendenti dai termini A, D non più peseranno egualmente sopra il punto C; perché la distanza del peso posto in D è fatta minor di quello che era mentre si ritrovava in B. Imperò che, se considereremo le linee per le quali i detti gravi fanno impeto, e discenderebbono quando liberamente si movessero, non è dubbio alcuno che sariano le linee AG, DF, BH: fa dunque momento ed impeto il peso pendente dal punto D secondo la linea DF; ma quando pendeva dal punto B, faceva impeto nella linea BH; e perché essa linea DF resta più vicina al sostegno C di quello che faccia la linea BH, perciò doviamo intendere, gli pesi pendenti dalli punti A, D non essere in distanze eguali dal punto C, ma sì bene quando saranno constituiti secondo la linea retta ACB. E finalmente si deve aver avvertenza di misurare le distanze con linee, che ad angoli retti caschino sopra quelle nelle quali i gravi stanno pendenti, e si moveriano quando liberamente scendessero.

Della stadera e della lieva...