click sulla figura qui sopra per tornare alla copertina

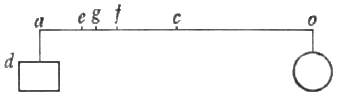
Sì come è assai noto a chi di leggere gli antichi scrittori cura si prende, avere Archimede trovato il furto dell'orefice nella corona d'oro di Ierone, così parmi esser stato sin ora ignoto il modo che sì grand'uomo usar dovesse in tale ritrovamento: atteso che il credere che procedesse, come da alcuni è scritto, co 'l mettere tal corona dentro a l'aqqua, avendovi prima posto altrettanto di oro purissimo e di argento separati, e che dalle differenze del far più o meno ricrescere o traboccare l'aqqua venisse in cognizione della mistione dell'oro con l'argento, di che tal corona era composta, par cosa, per così dirla, molto grossa e lontana dall'esquisitezza; e vie più parrà a quelli che le sottilissime invenzioni di sì divino uomo tra le memorie di lui aranno lette ed intese, dalle quali pur troppo chiaramente si comprende, quando tutti gli altri ingegni a quello di Archimede siano inferiori, e quanta poca speranza possa restare a qualsisia di mai poter ritrovare cose a quelle di esso simiglianti. Ben crederò io che, spargendosi la fama dell'aver Archimede ritrovato tal furto co 'l mezo dell'aqqua, fosse poi da qualche scrittore di quei tempi lasciata memoria di tal fatto; e che il medesimo, per aggiugner qualche cosa a quel poco che per fama avea inteso, dicesse Archimede essersi servito dell'aqqua nel modo che poi è stato dall'universal creduto. Ma il conoscer io che tal modo era in tutto fallace e privo di quella esattezza che si richiede nelle cose matematiche, mi ha più volte fatto pensare in qual maniera, co 'l mezo dell'aqqua, si potesse esquisitamente ritrovare la mistione di due metalli; e finalmente, dopo aver con diligenza riveduto quello che Archimede dimostra nei suoi libri Delle cose che stanno nell'aqqua ed in quelli Delle cose che pesano ugualmente, mi è venuto in mente un modo che esquisitissimamente risolve il nostro quesito: il qual modo crederò io esser l'istesso che usasse Archimede, atteso che, oltre all'esser esattissimo, depende ancora da dimostrazioni ritrovate dal medesimo Archimede.

Il modo è co 'l mezo di una bilancia, la cui fabbrica; ed uso qui apresso sarà posto, dopo che si averà dichiarato quanto a tale intelligenza è necessario. Devesi dunque prima sapere, che i corpi solidi che nell'aqqua vanno al fondo, pesano meno dell'aqqua che nell'aria tanto, quant'è nell'aria la gravità di tant'aqqua in mole quant'è esso solido: il che da Archimede è stato dimostrato; ma perché la sua dimostrazione è assai mediata, per non avere a procedere troppo in lungo, lasciandola da parte, con altri mezi lo dichiarerò. Consideriamo, dunque, che mettendo, per esempio, nell'aqqua una palla di oro, se tal palla fosse di aqqua, non peserebbe nulla, perché l'aqqua nell'aqqua non si muove in giù o in su. Resta dunque che tal [palla] di oro pesi nel[l'aqqua] quel tanto, in che la gravità dell'oro supera la gravità dell'aqqua; ed il simile si deve intendere de gli altri metalli: e perché i metalli son diversi tra di loro in gravità, secondo diverse proporzioni scemerà la lor gravità nell'aqqua. Come, per essempio, poniamo che l'oro pesi venti volte più dell'aqqua; è manifesto dalle cose dette, che l'oro peserà meno nell'aqqua che nell'aria la vigesima parte di tutta la sua gravità: supponiamo ora che l'argento, per esser men grave dell'oro, pesi 12 volte più che l'aqqua; questo, pesato nell'aqqua, scemerà in graveza per la duodecima parte: adunque meno scema nell'aqqua la gravità dell'oro che quella dell'argento, atteso che quella scema per un ventesimo e questa per un duodecimo. Se dunque in una bilancia esquisita noi appenderemo un metallo, e dall'altro braccio un contrapeso che pesi ugualmente co 'l detto metallo in aria; se poi tufferemo il metallo nell'aqqua, lasciando il contrapeso in aria; acciò detto contrapeso equivaglia al metallo, bisognerà ritirarlo verso il perpendicolo. Come, per essempio, sia la bilancia ab, il cui perpendicolo c; ed una massa di qualche metallo sia appesa in b, contrapesata dal peso d. Mettendo il peso b nell'aqqua, il peso d in a peserebbe più: però, acciò che pesasse ugualmente, bisognerebbe ritirarlo verso il perpendicolo c, come, v.g, in e; e quante volte la distanza ca supererà la ae, tante volte il metallo peserà più che l'aqqua. Poniamo dunque che il peso in b sia oro, e che pesato nell'aqqua torni il contrapeso d in e; e poi, facendo il medesimo dell'argento finissimo, che il suo contrapeso, quando si peserà poi nell'aqqua, torni in f: il qual punto sarà più vicino al punto c, sì come l'esperienza ne mostra, per esser l'argento men grave dell'oro; e la differenza che è dalla distanza af alla distanza ac sarà la medesima che la differenza tra la gravità dell'oro e quella de l'argento. Ma se noi aremo un misto di oro e di argento, è chiaro che, per participare di argento, peserà meno che l'oro puro, e, per participar di oro, peserà più che il puro argento: e però, pesato in aria, e volendo che il medesimo contrapeso lo contrapesi quando tal misto sarà tuffato nell'aqqua, sarà di mestiero ritirar detto contrapeso più verso il perpendicolo c che non è il punto e, il quale è il termine dell'oro, e medesimamente più lontano dal c che non è l'f, il quale è il termine dell'argento puro; però cascherà tra i termini e, f, e dalla proporzione nella quale verrà divisa la distanza ef si averà esquisitamente la proporzione dei due metalli, che tal misto compongono. Come, per esempio, intendiamo che il misto di oro ed argento sia in b, contrapesato in aria da d; il qual contrapeso, quando il misto sia posto nell'aqqua, ritorni in g: dico ora che l'oro e l'argento, che compongono tal misto, sono tra di loro nella medesima proporzione che le distanze fg, ge. Ma ci è da avvertire che la distanza gf, terminata nel segno dell'argento, ci denoterà la quantità dell'oro, e la distanza ge, terminata nel segno dell'oro, ci dimostrerà la quantità dell'argento: di maniera che se fg tornerà doppia di ge, il tal misto sarà due d'oro ed uno di argento. E col medesimo ordine procedendo nell'esamine di altri misti, si troverà esquisitamente la quantità dei semplici metalli.

Per fabricar dunque la bilancia, piglisi un regolo lungo almeno due braccia, e quanto più sarà lungo più sarà esatto l'istrumento; e dividasi nel mezo, dove si ponga il perpendicolo; poi si aggiustino le braccia che stiano nell'equilibrio, con l'assottigliare quello che pesasse più; e sopra l'uno delle braccia si notino i termini [dove ritor]nano i contrapesi de i metalli semplici quando saranno pesati nell'aqqua, avvertendo di pesare i metalli più puri che si trovino. Fatto che sarà questo, resta a ritrovar modo col quale si possa con facilità aver la proporzione, [secondo la quale] le distanze tra i termini de i metalli puri verra[nno] divise da i segni de i misti. Il che, al mio giudizio, si conseguirà in questo modo:

Sopra i termini de i metalli semplici avvolgasi un sol filo di corda di acciaio sottilissima; ed intorno agli intervalli, che tra i termini rimangono, avvolgasi un filo di ottone pur sottilissimo; e verranno tali distanze divise in molte particelle uguali. Come, per essempio, sopra i termini e, f avvolgo 2 fili solo di acciaio (e questo per distinguerli dall'ottone); e poi vo riempiendo tutto lo spazio tra e, f con l'avvolgervi un filo sottilissimo di ottone, il quale mi dividerà lo spazio ef in molte particelle uguali; poi, quando io vorrò sapere la proporzione che è tra fg e ge, conterò i fili fg ed i fili ge, e, trovando i fili fg esser 40 ed i ge esser, per essempio, 21, dirò nel misto esser 40 di oro e 21 di argento.

Ma qui è da avvertire che nasce una difficultà nel contare: però che, per essere quei fili sottilissimi, come si richiede all'esquisitezza, non è possibile con la vista numerarli, però che tra sì piccoli spazii si abbaglia l'occhio. Adunque, per numerargli con facilità, piglisi uno stiletto acutissimo, col quale si vada adagio adagio discorrendo sopra detti fili; ché così, parte mediante l'udito, parte mediante il ritrovar la mano ad ogni filo l'impedimento, verranno con facilità detti fili numerati: dal numero de i quali, come ho detto di sopra, si averà l'esquisita quantità de i semplici, de' quali è il misto composto. Avvertendo però, che i semplici risponderanno contrariamente alle distanze: come, per esempio, in un misto d'oro e d'argento, i fili che saranno verso il termine dell'argento ci daranno la quantità dell'oro, e quelli che saranno verso 'l termine dell'oro ci dimostreranno la quantità dell'argento; ed il medesimo intendasi degli altri misti.

- FINE -