Galileo Galilei

DISCORSI E DIMOSTRAZIONI MATEMATICHE
INTORNO A DUE NUOVE SCIENZE
ATTENENTI ALLA MECANICA & I MOVIMENTI LOCALI

GIORNATA PRIMA

Interlocutori:
Salviati, Sagredo e Simplicio

Salv. Largo campo di filosofare a gl'intelletti specolativi parmi che porga la frequente pratica del famoso arsenale di voi, Signori Veneziani, ed in particolare in quella parte che mecanica si domanda; atteso che quivi ogni sorte di strumento e di machina vien continuamente posta da numero grande d'artefici, tra i quali, e per l'osservazioni fatte dai loro antecessori, e per quelle che di propria avvertenza vanno continuamente per se stessi facendo, è forza che ve ne siano de i peritissimi e di finissimo discorso.

Sagr. V. S. non s'inganna punto: ed io, come per natura curioso, frequento per mio diporto la visita di questo luogo e la pratica di questi che noi, per certa preminenza che tengono sopra 'l resto della maestranza, domandiamo proti; la conferenza de i quali mi ha più volte aiutato nell'investigazione della ragione di effetti non solo maravigliosi, ma reconditi ancora e quasi inopinabili. È vero che tal volta anco mi ha messo in confusione ed in disperazione di poter penetrare come possa seguire quello che, lontano da ogni mio concetto, mi dimostra il senso esser vero. E pur quello che poco fa ci diceva quel buon vecchio è un dettato ed una proposizione ben assai vulgata; ma però io la reputava in tutto vana, come molte altre che sono in bocca de i poco intelligenti, credo da loro introdotte per mostrar di saper dir qualche cosa intorno a quello di che non son capaci.

Salv. V. S. vuol forse dire di quell'ultimo pronunziato ch'ei profferì mentre ricercavamo d'intendere per qual ragione facevano tanto maggior apparecchio di sostegni, armamenti ed altri ripari e fortificazioni, intorno a quella gran galeazza che si doveva varare, che non si fa intorno a vasselli minori; dove egli rispose, ciò farsi per evitare il pericolo di direnarsi, oppressa dal gravissimo peso della sua vasta mole, inconveniente al quale non son soggetti i legni minori?

Sagr. Di cotesto intendo, e sopra tutto dell'ultima conclusione ch'ei soggiunse, la quale io ho sempre stimata concetto vano del vulgo; cioè che in queste ed altre simili machine non bisogna argumentare dalle piccole alle grandi, perché molte invenzioni di machine riescono in piccolo, che in grande poi non sussistono. Ma essendo che tutte le ragioni della mecanica hanno i fondamenti loro nella geometria, nella quale non veggo che la grandezza e la piccolezza faccia i cerchi, i triangoli, i cilindri, i coni e qualunque altre figure solide, soggette ad altre passioni queste e ad altre quelle; quando la machina grande sia fabricata in tutti i suoi membri conforme alle proporzioni della minore, che sia valida e resistente all'esercizio al quale ella è destinata, non so vedere perché essa ancora non sia esente da gl'incontri che sopraggiugner gli possono, sinistri e destruttivi.

Salv. Il detto del vulgo è assolutamente vano; e talmente vano, che il suo contrario si potrà profferire con altrettanta verità, dicendo che molte machine si potranno far più perfette in grande che in piccolo: come, per esempio, un oriuolo, che mostri e batta le ore, più giusto si farà d'una tal grandezza che di un'altra minore. Con miglior fondamento usurpano quel medesimo detto altri più intelligenti, i quali della riuscita di tali machine grandi, non conforme a quello che si raccoglie dalle pure ed astratte dimostrazioni geometriche, ne rimettono la causa nell'imperfezzione della materia, che soggiace a molte alterazioni ed imperfezzioni. Ma qui non so s'io potrò, senza inciampare in qualche nota di arroganza, dire che né anco il ricorrere all'imperfezzioni della materia, potenti a contaminare le purissime dimostrazioni matematiche, basti a scusare l'inobbedienza delle machine in concreto alle medesime astratte ed ideali: tuttavia io pure il dirò, affermando che, astraendo tutte l'imperfezzioni della materia e supponendola perfettissima ed inalterabile e da ogni accidental mutazione esente, con tutto ciò il solo esser materiale fa che la machina maggiore, fabbricata dell'istessa materia e con l'istesse proporzioni che la minore, in tutte l'altre condizioni risponderà con giusta simmetria alla minore, fuor che nella robustezza e resistenza contro alle violente invasioni; ma quanto più sarà grande, tanto a proporzione sarà più debole. E perché io suppongo, la materia essere inalterabile, cioè sempre l'istessa, è manifesto che di lei, come di affezzione eterna e necessaria, si possano produr dimostrazioni non meno dell'altre schiette e pure matematiche. Però, Sig. Sagredo, revochi pur l'opinione che teneva, e forse insieme con molti altri che nella mecanica han fatto studio, che le machine e le fabbriche composte delle medesime materie, con puntuale osservanza delle medesime proporzioni tra le loro parti, debban essere egualmente, o, per dir meglio, proporzionalmente, disposte al resistere ed al cedere alle invasioni ed impeti esterni, perché si può geometricamente dimostrare, sempre le maggiori essere a proporzione men resistenti che le minori; sì che ultimamente non solo di tutte le machine e fabbriche artifiziali, ma delle naturali ancora, sia un termine necessariamente ascritto, oltre al quale né l'arte né la natura possa trapassare: trapassar, dico, con osservar sempre l'istesse proporzioni con l'identità della materia.

Sagr. Io già mi sento rivolgere il cervello, e, quasi nugola dal baleno repentinamente aperta, ingombrarmisi la mente da momentanea ed insolita luce, che da lontano mi accenna e subito confonde ed asconde imaginazioni straniere ed indigeste. E da quanto ella ha detto parmi che dovrebbe seguire che fusse impossibil cosa costruire due fabbriche dell'istessa materia simili e diseguali, e tra di loro con egual proporzione resistenti; e quando ciò sia, sarà anco impossibile trovar due sole aste dell'istesso legno tra di loro simili in robustezza e valore, ma diseguali in grandezza.

Salv. Così è, Sig. Sagredo: e per meglio assicurarci che noi convenghiamo nel medesimo concetto, dico che se noi ridurremo un'asta di legno a tal lunghezza e grossezza, che fitta, v. g., in un muro ad angoli retti, cioè parallela all'orizonte, sia ridotta all'ultima lunghezza che si possa reggere, sì che, allungata un pelo più, si spezzasse, gravata dal proprio peso, questa sarà unica al mondo; tal che essendo, per esempio, la sua lunghezza centupla della sua grossezza, nissuna altra asta della medesima materia potrà ritrovarsi che, essendo in lunghezza centupla della sua grossezza, sia, come quella, precisamente abile a sostener se medesima, e nulla di più; ma tutte le maggiori si fiaccheranno, e le minori saranno potenti a sostener, oltre al proprio peso, qualch'altro appresso. E questo che io dico dello stato di regger se medesimo, intendasi detto di ogni altra costituzione; e così se un corrente potrà reggere il peso di dieci correnti suoi eguali, una trave simile a lui non potrà altramente regger il peso di dieci sue eguali. Ma notino in grazia V. S. e 'l Sig. Simplicio nostro, quanto le conclusioni vere, benché nel primo aspetto sembrino improbabili, additate solamente qualche poco, depongono le vesti che le occultavano, e nude e semplici fanno de' lor segreti gioconda mostra. Chi non vede come un cavallo cadendo da un'altezza di tre braccia o quattro si romperà l'ossa, ma un cane da una tale, e un gatto da una di otto o dieci, non si farà mal nissuno, come né un grillo da una torre, né una formica precipitandosi dall'orbe lunare? i piccoli fanciulli restare illesi in cadute, dove i provetti si rompono gli stinchi o la testa? E come gli animali più piccoli sono, a proporzione, più robusti e forti de i maggiori, così le piante minori meglio si sostentano: e già credo che amendue voi apprendiate che una quercia dugento braccia alta non potrebbe sostenere i suoi rami sparsi alla similitudine di una di mediocre grandezza, e che la natura non potrebbe fare un cavallo grande per venti cavalli, né un gigante dieci volte più alto di un uomo, se non o miracolosamente o con l'alterar assai le proporzioni delle membra ed in particolare dell'ossa, ingrossandole molto sopra la simmetria dell'ossa comuni. Il creder parimente che nelle machine artifiziali egualmente siano fattibili e conservabili le grandissime e le piccole, è errore manifesto: e così, per esempio, piccole guglie, colonnette ed altre solide figure, sicuramente si potranno maneggiare distendere e rizzare, senza risico di rompersi, che le grandissime per ogni sinistro accidente andranno in pezzi, e non per altra cagione che per il loro proprio peso. E qui è forza che io vi racconti un caso degno veramente di esser saputo, come sono tutti gli accidenti che accascano fuori dell'aspettazione, e massime quando il partito preso per ovviare a uno inconveniente riesce poi causa potissima del disordine. Era una grossissima colonna di marmo distesa, e posata, presso alle sue estremità, sopra due pezzi di trave; cadde in pensiero dopo certo tempo ad un mecanico che fusse bene, per maggiormente assicurarsi che gravata dal proprio peso non si rompesse nel mezzo, supporgli anco in questa parte un terzo simile sostegno: parve il consiglio generalmente molto opportuno, ma l'esito lo dimostrò essere stato tutto l'opposito, atteso che non passarono molti mesi che la colonna si trovò fessa e rotta, giusto sopra il nuovo appoggio di mezzo.

Simp. Accidente in vero maraviglioso e veramente praeter spem, quando però fusse derivato dall'aggiungervi il nuovo sostegno di mezzo.

Salv. Da quello sicuramente derivò egli, e la riconosciuta cagion dell'effetto leva la maraviglia: perché, deposti in piana terra i due pezzi della colonna, si vedde che l'uno de i travi, su 'l quale appoggiava una delle testate, si era, per la lunghezza del tempo, infracidato ed avvallato, e, restando quel di mezzo durissimo e forte, fu causa che la metà della colonna restasse in aria, abbandonata dall'estremo sostegno; onde il proprio soverchio peso gli fece fare quello che non avrebbe fatto se solo sopra i due primi si fusse appoggiata, perché l'avvallarsi qual si fusse di loro, ella ancora l'arebbe seguito. E qui non si può dubitare che tal accidente non sarebbe avvenuto in una piccola colonna, benché della medesima pietra e di lunghezza rispondente alla sua grossezza con la proporzione medesima della grossezza e lunghezza della colonna grande.

Sagr. Già sin qui resto io assicurato della verità dell'effetto ma non penetro già la ragione come, nel crescersi la materia, non deva con l'istesso ragguaglio multiplicarsi la resistenza e gagliardia; e tanto più mi confondo, quanto per l'opposito veggo in altri casi crescersi molto più la robustezza e la resistenza al rompersi, che non cresce l'ingrossamento della materia: che se, v. g., saranno due chiodi fitti in un muro, l'uno più grosso il doppio dell'altro, quello reggerà non solamente doppio peso di questo, ma triplo e quadruplo.

Salv. Dite pur ottuplo, né direte lontano dal vero: né questo effetto contraria a quello, ancor che in sembiante apparisca così diverso.

Sagr. Adunque, Sig. Salviati, spianateci questi scogli e dichiarateci queste oscurità, se ne avete il modo, ché ben conietturo, questa materia delle resistenze essere un campo pieno di belle ed utili contemplazioni; e se vi contentate che questo sia il soggetto de i nostri ragionamenti di oggi, a me, e credo al Sig. Simplicio, sarà gratissimo.

Salv. Non posso mancar di servirle, purché la memoria serva me in sumministrarmi quello che già appresi dal nostro Accademico, che sopra tal materia aveva fatte molte speculazioni, e tutte, conforme al suo solito, geometricamente dimostrate, in modo che, non senza ragione, questa sua potrebbe chiamarsi una nuova scienza; perché se bene alcune delle conclusioni sono state da altri, e prima di tutti da Aristotele, osservate, tuttavia né sono delle più belle, né (quello che più importa) da i loro primarii e indubitati fondamenti con necessarie dimostrazioni provate. E perché, come dico, voglio dimostrativamente accertarvi, e non con solamente probabili discorsi persuadervi, supponendo che abbiate quella cognizione delle conclusioni mecaniche, da altri sin qui fondatamente trattate, che per il nostro bisogno sarà necessaria, conviene che avanti ogni altra cosa consideriamo qual effetto sia quello che si opera nella frazzione di un legno o di altro solido, le cui parti saldamente sono attaccate; perché questa è la prima nozione, nella qual consiste il primo e semplice principio che come notissimo conviene supporsi.

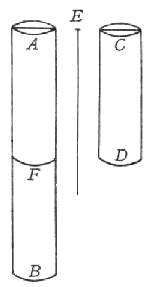
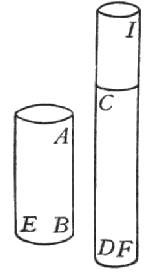
Per più chiara esplicazione di che, segniamo il cilindro o prisma AB di legno o di altra materia solida e coerente, fermato di sopra in A e pendente a piombo, al quale nell'altra estremità B sia attaccato il peso C: è manifesto che, qualunque si sia la tenacità e coerenza tra di loro delle parti di esso solido, pur che non sia infinita, potrà esser superata dalla forza del traente peso C, la cui gravità pongo che possa accrescersi quanto ne piace, e esso solido finalmente si strapperà, a guisa d'una corda. E sì come nella corda noi intendiamo, la sua resistenza derivare dalla moltitudine delle fila della canapa che la compongono, così nel legno si scorgono le sue fibre e filamenti distesi per lungo, che lo rendono grandemente più resistente allo strappamento che non sarebbe qualsivoglia canapo della medesima grossezza: ma nel cilindro di pietra o di metallo la coerenza (che ancora par maggiore) delle sue parti depende da altro glutine che da filamenti o fibre; e pure essi ancora da valido tiramento vengono spezzati.

Simp. Se il negozio procede come voi dite, intendo bene che i filamenti nel legno, che son lunghi quanto l'istesso legno, posson renderlo gagliardo e resistente a gran forza che se gli faccia per romperlo; ma una corda composta di fili di canapa non più lunghi di due o tre braccia l'uno, come potrà ridursi alla lunghezza di cento, restando tanto gagliarda? In oltre vorrei anco sentire la vostra opinione intorno all'attaccamento delle parti de i metalli, delle pietre e di altre materie prive di tali filamenti, che pur, s'io non m'inganno, è anco più tenace.

Salv. In nuove specolazioni, e non molto al nostro intento necessarie, converrà divertire, se dovremo delle promosse difficoltà portar le soluzioni.

Sagr. Ma se le digressioni possono arrecarci la cognizione di nuove verità, che pregiudica a noi, non obbligati a un metodo serrato e conciso, ma che solo per proprio gusto facciamo i nostri congressi, digredir ora per non perder quelle notizie che forse, lasciata l'incontrata occasione, un'altra volta non ci si rappresenterebbe? anzi chi sa che bene spesso non si possano scoprir curiosità più belle delle primariamente cercate conclusioni? Pregovi per tanto io ancora a dar sodisfazione al Sig. Simplicio ed a me, non men di esso curioso e desideroso d'intender qual sia quel glutine che sì tenacemente ritien congiunte le parti de i solidi, che pur finalmente sono dissolubili: cognizione che pur anco è necessaria per intender la coerenza delle parti de gli stessi filamenti, de i quali alcuni de i solidi son composti.

Salv. Eccomi a servirvi, poiché così vi piace. È la prima difficoltà, come possano i filamenti d'una corda lunga cento braccia sì saldamente connettersi insieme (non essendo ciascheduno di essi lungo più di due o tre), che gran violenza ci voglia a disseparargli. Ma ditemi, Sig. Simplicio: non potreste voi d'un sol filo di canapa tener l'una dell'estremità talmente stretta fra le dita, che io, tirando dall'altra, prima che liberarlo dalla vostra mano, lo rompessi? Certo sì. Quando dunque i fili della canapa fusser non solo nell'estremità, ma in tutta la lor lunghezza, con gran forza da chi gli circondasse tenuti stretti, non è manifesta cosa che lo sbarbargli da chi gli strigne sarebbe assai più difficile che il rompergli? Ma nella corda l'istesso atto dell'attorcerla strigne le fila scambievolmente tra di loro in maniera, che tirando poi con gran forza la fune, i suoi filamenti si spezzano, e non si separano l'uno dall'altro; come manifestamente si conosce dal vedersi nella rottura i filamenti cortissimi, e non lunghi almeno un braccio l'uno, come dovria vedersi quando la division della corda si facesse non per lo strappamento delle fila, ma per la sola separazione dell'uno dall'altro strisciando.

Sagr. Aggiungasi, in confermazion di questo, il vedersi tal volta romper la corda non per il tirarla per lo lungo, ma solo per il soverchiamente attorcerla: argumento, par a me, concludente, le fila esser talmente tra di loro scambievolmente compresse, che le comprimenti non permettono alle compresse scorrer quel minimo che, che sarebbe necessario per allungar le spire, acciò potessero circondar la fune che nel torcimento si scorcia ed in consequenza qualche poco s'ingrossa.

Salv. Voi benissimo dite: ma considerate appresso come una verità si tira dietro l'altra. Quel filo che stretto tra le dita non segue chi, con qualche forza tirandolo, vorrebbe di tra esse sottrarlo, resiste perché da doppia compressione vien ritenuto; avvenga che non meno il dito superiore preme contro l'inferiore, che questo si prema contro a quello. E non è dubbio che quando di queste due premure se ne potesse ritenere una sola, resterebbe la metà di quella resistenza che dalle due congiunte dependeva; ma perché non si può con l'alzar, v. g., il dito superiore levar la sua pressione senza rimuover anco l'altra parte, conviene con nuovo artifizio conservarne una di loro, e trovar modo che l'istesso filo comprima se medesimo contro al dito o altro corpo solido sopra 'l quale si posa, e far sì che l'istessa forza che lo tira per separarnelo, tanto più ve lo comprima, quanto più gagliardamente lo tira: e questo si conseguirà con l'avvolgere a guisa di spira il filo medesimo intorno al solido; il che acciò meglio s'intenda, ne segnerò un poco di figura.

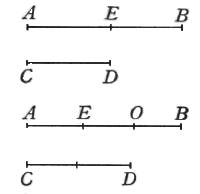
E questi AB, CD siano due cilindri, e tra essi disteso il filo EF, che per maggior chiarezza ce lo figureremo essere una cordicella: non è dubbio, che premendo gagliardamente i due cilindri l'uno contro all'altro, la corda FE, tirata dall'estremità F, resisterà a non piccola violenza prima che scorrere tra i due solidi comprimentila; ma se rimuoveremo l'uno di loro, la corda, benché continui di toccar l'altro, non però da tal toccamento sarà ritenuta che liberamente non scorra. Ma se ritenendola, benché debolmente attaccata verso la sommità del cilindro A, l'avvolgeremo intorno a quello a foggia di spira AFLOTR, e dal capo R la tireremo, è manifesto che ella comincerà a stringere il cilindro; e se le spire e volute saranno molte, sempre più, nel validamente tirare, si comprimerà la corda addosso al cilindro; e facendosi, con la multiplicazione delle spire, più lungo il toccamento, ed in consequenza men superabile, difficile si farà sempre più lo scorrer della corda e l'acconsentir alla traente forza. Or chi non vede che tale è la resistenza delle filamenta, che con mille e mille simili avvolgimenti il grosso canapo contessono? Anzi lo strignimento di simili tortuosità collega tanto tenacemente, che di non molti giunchi, né anco molto lunghi, sì che poche son le spire con le quali tra di loro s'intrecciano, si compongono robustissime funi, che mi par che domandino suste.

Sagr. Cessa per il vostro discorso nella mia mente la maraviglia di due effetti, de i quali le ragioni non bene erano comprese da me. Uno era il vedere come due o al più tre rivolte del canapo intorno al fuso dell'argano potevano non solamente ritenerlo, che, tirato dall'immensa forza del peso che ei sostiene, scorrendo non gli cedesse, ma che di più, girando l'argano, il medesimo fuso, col solo toccamento del canapo che lo strigne, potesse con li succedenti ravvolgimenti tirare e sollevare vastissime pietre, mentre che le braccia d'un debile ragazzo vanno ritenendo e radunando l'altro capo del medesimo canapo. L'altro è d'un semplice ma arguto ordigno, trovato da un giovane mio parente, per poter con una corda calarsi da una finestra senza scorticarsi crudelmente le palme delle mani, come poco tempo avanti gli era intervenuto con sua grandissima offesa. Ne farò, per facile intelligenza, un piccolo schizzo.

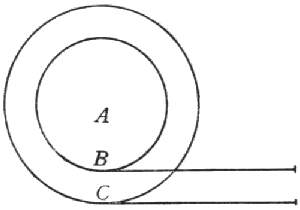
Intorno a un simil cilindro di legno AB, grosso come una canna e lungo circa un palmo, incavò un canaletto in forma di spira, di una voluta e mezo e non più, e di larghezza capace della corda che voleva adoprare; e questa fece entrare per il canale dal termine A ed uscire per l'altro B, circondando poi tal cilindro e corda con un cannone pur di legno, o vero anco di latta, ma diviso per lungo ed ingangherato, sì che liberamente potesse aprirsi e chiudersi: ed abbracciando poi e strignendo con ambe le mani esso cannone, raccomandata la corda a un fermo ritegno di sopra, si sospese su le braccia; e riuscì tale la compressione della corda tra 'l cannone ambiente e 'l cilindro, che, ad arbitrio suo, strignendo fortemente le mani poteva sostenersi senza calare ed allentandole un poco si calava lentamente a suo piacimento.

Salv. Ingegnosa veramente invenzione; e per intera esplicazione della sua natura, mi par di scorgere così per ombra che qualche altra specolazione si potesse aggiugnere: ma non voglio per ora digredir più sopra di questo particolare, e massime volendo voi sentir il mio pensiero intorno alla resistenza allo strapparsi de gli altri corpi, la cui testura non è di filamenti, come quella delle funi e della maggior parte de i legni; ma la coerenza delle parti loro in altre cagioni par che consista, le quali, per mio giudizio, si riducono a due capi: l'uno de i quali è quella decantata repugnanza che ha la natura all'ammettere il vacuo; per l'altro bisogna (non bastando questo del vacuo) introdur qualche glutine, visco o colla, che tenacemente colleghi le particole delle quali esso corpo è composto. Dirò prima del vacuo, mostrando con chiare esperienze quale e quanta sia la sua virtù. E prima, il vedersi, quando ne piaccia, due piastre di marmo, di metallo o di vetro, esquisitamente spianate pulite e lustre, che, posata l'una su l'altra, senza veruna fatica se gli muove sopra strisciando (sicuro argumento che nissun glutine le congiugne), ma che volendo separarle, mantenendole equidistanti, tal repugnanza si trova, che la superiore solleva e si tira dietro l'altra e perpetuamente la ritiene sollevata, ancorché assai grossa e grave, evidentemente ci mostra l'orrore della natura nel dover ammettere, se ben per breve momento di tempo, lo spazio voto che tra di quelle rimarrebbe avanti che il concorso delle parti dell'aria circostante l'avesse occupato e ripieno. Vedesi anco, che quando bene tali due lastre non fussero esattamente pulite, e perciò che il lor contatto non fusse esquisito del tutto, nel volerle separar lentamente niuna renitenza si trova fuor di quella della sola gravità; ma in un alzamento repentino l'inferior pietra si solleva, ma subito ricade, seguendo solamente la sovrana per quel brevissimo tempo che basta per la distrazzione di quella poca d'aria che s'interponeva tra le lastre, che non ben combaciavano, e per l'ingresso dell'altra circunfusa. Tal resistenza, che così sensatamente si scorge tra le due lastre, non si può dubitare che parimente non risegga tra le parti di un solido, e che nel loro attaccamento non entri almanco a parte e come causa concomitante.

Sagr. Fermate di grazia, e concedetemi ch'io dica una particolar considerazione che pur ora mi è caduta in mente: e questa è, che il vedere come la piastra inferiore segue la superiore e che con moto velocissimo vien sollevata, ci rende sicuri che, contro al detto di molti filosofi e forse d'Aristotele medesimo, il moto nel vacuo non sarebbe instantaneo; perché quando fusse tale, le nominate due lastre senza repugnanza veruna si separerebbero, già che il medesimo instante di tempo basterebbe per la loro separazione e per il concorso dell'aria ambiente a riempier quel vacuo che tra esse potesse restare. Dal seguir dunque che fa l'inferior lastra la superiore, si raccoglie come nel vacuo il moto non sarebbe instantaneo; e si raccoglie insieme che pur tra le medesime piastre resti qualche vacuo, almeno per brevissimo tempo, cioè per tutto quello che passa nel movimento dell'ambiente, mentre concorre a riempiere il vacuo; ché se vacuo non vi restasse, né di concorso né di moto di ambiente vi sarebbe bisogno. Converrà dunque dire che, pur per violenza o contro a natura, il vacuo talor si conceda (benché l'opinion mia è che nissuna cosa sia contro a natura, salvo che l'impossibile, il quale poi non è mai). Ma qui mi nasce un'altra difficoltà; ed è che, se ben l'esperienza m'assicura della verità della conclusione, l'intelletto non resta già interamente appagato della causa alla quale cotale effetto viene attribuito. Imperò che l'effetto della separazione delle due lastre è anteriore al vacuo, che in consequenza alla separazione succederebbe: e perché mi pare che la causa debba, se non di tempo, almeno di natura precedere all'effetto, e che d'un effetto positivo positiva altresì debba esser la causa, non resto capace come dell'aderenza delle due piastre e della repugnanza all'esser separate, effetti che già sono in atto, si possa referir la cagione al vacuo, che non è, ma che arebbe a seguire; e delle cose che non sono, nussuna può esser l'operazione, conforme al pronunziato certissimo del Filosofo.

Simp. Ma già che concedete questo assioma ad Aristotele, non credo che siate per negargliene un altro, bellissimo e vero: e questo è, che la natura non intraprende a voler fare quello che repugna ad esser fatto, dal qual pronunziato mi par che dependa la soluzione del vostro dubbio. Perché dunque a se medesimo repugna essere uno spazio vacuo, vieta la natura il far quello in consequenza di che necessariamente succederebbe il vacuo; e tale è la separazione delle due lastre.

Sagr. Ora, ammesso per soluzione adequata del mio dubbio questo che produce il Sig. Simplicio, seguitando il cominciato discorso, parmi che questa medesima repugnanza al vacuo devrebbe esser bastante ritegno delle parti di un solido di pietra o di metallo, o se altre ve ne sono che più saldamente stiano congiunte e renitenti alla divisione. Perché, se di uno effetto una sola è la cagione, sì come io ho inteso e creduto, o, se pur molte se n'assegnano, ad una sola si riducono, perché questa del vacuo, che sicuramente è, non basterà per tutte le resistenze?

Salv. Io per ora non voglio entrare in questa contesa, se il vacuo senz'altro ritegno sia per sé solo bastante a tenere unite le parti disunibili de i corpi consistenti; ma vi dico bene che la ragione del vacuo, che milita e conclude nelle due piastre, non basta per sé sola al saldo collegamento delle parti di un solido cilindro di marmo o di metallo, le quali, violentate da forze gagliarde che dirittamente le tirino, finalmente si separano e si dividono. E quando io trovi modo di distinguer questa già conosciuta resistenza, dependente dal vacuo, da ogni altra, qualunque ella si fusse, che con lei concorresse in fortificar l'attaccamento, e che io vi faccia vedere come essa sola non sia a gran pezzo bastante per tale effetto, non concederete voi che sia necessario introdurne altra? Aiutatelo, Sig. Simplicio, già che egli sta ambiguo sopra quello che debba rispondere.

Simp. È forza che la sospensione del Sig. Sagredo sia per altro rispetto, non restando luogo di dubitare sopra sì chiara e necessaria consequenza.

Sagr. Voi, Sig. Simplicio, l'avete indovinata. Andavo pensando se, non bastando un million d'oro l'anno, che vien di Spagna, per pagar l'esercito, fusse necessario far altra provisione che di danari per le paghe de' soldati. Ma seguitate pur, Sig. Salviati, e supponendo ch'io ammetta la vostra consequenza, mostrateci il modo di separare l'operazione del vacuo dall'altre, e misurandola fateci vedere come ella sia scarsa per l'effetto di che si parla.

Salv. Il vostro demonio vi assiste. Dirò il modo dell'appartar la virtù del vacuo dall'altre, e poi la maniera del misurarla. E per appartarla, piglieremo una materia continua, le cui parti manchino di ogni altra resistenza alla separazione fuor che di quella del vacuo, quale a lungo è stato dimostrato in certo trattato del nostro Accademico esser l'acqua: talché, qualunque volta si disponesse un cilindro d'acqua, e che, attratto, si sentisse resistenza allo staccamento delle sue parti, questo da altra cagione che dalla repugnanza al vacuo non potrebbe riconoscersi. Per far poi una tale esperienza mi son immaginato un artifizio, il quale con l'aiuto di un poco di disegno, meglio che con semplici parole, potrò dichiarare.

Figuro, questo CABD essere il profilo di un cilindro di metallo o di vetro, che sarebbe meglio, voto dentro, ma giustissimamente tornito, nel cui concavo entri con esquisitissimo contatto un cilindro di legno, il cui profilo noto EGHF, il qual cilindro si possa spignere in su e 'n giù; e questo voglio che sia bucato nel mezzo, sì che vi passi un filo di ferro, oncinato nell'estremità K, e l'altro capo I vadia ingrossandosi in forma di cono o turbine, facendo che il foro fatto nel legno sia nella parte di sopra esso ancora incavato in forma di conica superficie, aggiustata puntualmente per ricevere la conica estremità I del ferro IK, qualunque volta si tiri giù dalla parte K. Inserto il legno, o vogliamolo chiamar zaffo, EH nel cavo cilindro AD, non voglio ch'arrivi sino alla superior superficie di esso cilindro, ma che resti lontano due o tre dita; e tale spazio deve esser ripieno di acqua, la quale vi si metterà tenendo il vaso con la bocca CD all'in su e calcandovi sopra il zaffo EH, col tenere il turbine I remoto alquanto dal cavo del legno per lasciar l'esito all'aria, che nel calcare il zaffo se n'uscirà per il foro del legno, che perciò si fa alquanto più largo della grossezza dell'asticciuola di ferro IK. Dato l'esito all'aria e ritirato il ferro, che ben suggelli su 'legno col suo turbine I, si rivolterà il vaso tutto con la bocca all'in giù, ed attaccando all'oncino K un recipiente da mettervi dentro rena o altra materia grave, si caricherà tanto, che finalmente la superior superficie EF del zaffo si staccherà dall'inferiore dell'acqua, alla quale niente altro la teneva congiunta che la repugnanza del vacuo; pesando poi il zaffo col ferro col recipiente e con ciò che vi sarà dentro, aremo la quantità della forza del vacuo: e se, attaccato a un cilindro di marmo o di cristallo, grosso quanto il cilindro dell'acqua, peso tale che, insieme col peso proprio dell'istesso marmo o cristallo, pareggi la gravità di tutte le nominate bagaglie, ne seguirà la rottura, potremo senza verun dubbio affermare, la sola ragion del vacuo tener le parti del marmo e cristallo congiunte; ma non bastando, e che per romperlo bisogni aggiugnervi quattro volte altrettanto peso, converrà dire, la resistenza del vacuo esser delle cinque parti una, e l'altra quadrupla di quella del vacuo.

Simp. Non si può negare che l'invenzione non sia ingegnosa, ma l'ho per soggetta a molte difficoltà, che me la rendono dubbia: perché, chi ci assicura che l'aria non possa penetrar tra 'l vetro e 'l zaffo, ancorché si circondi bene di stoppa o altra materia cedente? e così, acciò che il cono I saldi bene il foro, forse non basterebbe l'ugnerlo con cera o trementina. In oltre, perché non potrebbero le parti dell'acqua distrarsi e rarefarsi? perché non penetrare aria, o esalazioni, o altre sustanze più sottili, per le porosità del legno, o anche dell'istesso vetro?

Salv. Molto destramente ci muove il Sig. Semplicio le difficoltà, ed in parte ci sumministra i rimedii, quanto alla penetrazion dell'aria per il legno, o tra 'l legno e 'l vetro. Ma io, oltre di ciò, noto che potremo nell'istesso tempo accorgerci, con acquisto di nuove cognizioni, se le promosse difficoltà aranno luogo. Imperò che, se l'acqua sarà per natura, se ben con violenza, distraibile, come accade nell'aria, si vedrà il zaffo calare; e se faremo nella parte superiore del vetro un poco di ombelico prominente, come questo V, penetrando, per la sustanza o porosità del vetro o del legno, aria o altra più tenue e spiritosa materia, si vedrà radunare (cedendogli l'acqua) nell'eminenza V: le quali cose quando non si scorgano, verremo assicurati, l'esperienza esser con le debite cautele stata tentata; e conosceremo, l'acqua non esser distraibile, né il vetro esser permeabile da veruna materia, benché sottilissima.

Sagr. Ed io mercé di questi discorsi ritrovo la causa di un effetto che lungo tempo m'ha tenuto la mente ingombrata di maraviglia e vota d'intelligenza. Osservai già una citerna, nella quale, per trarne l'acqua, fu fatta fare una tromba, da chi forse credeva, ma vanamente, di poterne cavar con minor fatica l'istessa o maggior quantità che con le secchie ordinarie; ed ha questa tromba il suo stantuffo e animella su alta, sì che l'acqua si fa salire per attrazzione, e non per impulso, come fanno le trombe che hanno l'ordigno da basso. Questa, sin che nella citerna vi è acqua sino ad una determinata altezza, la tira abbondantemente; ma quando l'acqua abbassa oltre a un determinato segno, la tromba non lavora più. Io credetti, la prima volta che osservai tale accidente, che l'ordigno fusse guasto; e trovato il maestro acciò lo raccomodasse, mi disse che non vi era altrimente difetto alcuno, fuor che nell'acqua, la quale, essendosi abbassata troppo, non pativa d'esser alzata a tanta altezza; e mi soggiunse, né con trombe, né con altra machina che sollevi l'acqua per attrazzione, esser possibile farla montare un capello più di diciotto braccia: e siano le trombe larghe o strette, questa è la misura dell'altezza limitatissima. Ed io sin ora sono stato così poco accorto, che, intendendo che una corda, una mazza di legno e una verga di ferro, si può tanto e tanto allungare che finalmente il suo proprio peso la strappi, tenendola attaccata in alto, non mi è sovvenuto che l'istesso, molto più agevolmente, accaderà di una corda o verga di acqua. E che altro è quello che si attrae nella tromba, che un cilindro di acqua, il quale, avendo la sua attaccatura di sopra, allungato più e più, finalmente arriva a quel termine oltre al quale, tirato dal suo già fatto soverchio peso, non altrimente che se fusse una corda, si strappa?

Salv. Così puntualmente cammina il negozio; e perché la medesima altezza delle diciotto braccia è il prefisso termine dell'altezza alla quale qualsivoglia quantità d'acqua, siano cioè le trombe larghissime o strette o strettissime quanto un fil di paglia, può sostentarsi, tutta volta che noi peseremo l'acqua contenuta in diciotto braccia di cannone, sia largo o stretto, aremo il valore della resistenza del vacuo ne i cilindri di qualsivoglia materia solida, grossi quanto sono i concavi de i cannoni proposti. E già che aviamo detto tanto, mostriamo come di tutti i metalli, pietre, legni, vetri, etc., si può facilmente ritrovare sino a quanta lunghezza si potrebbono allungare cilindri, fili o verghe di qualsivoglia grossezza, oltre alla quale, gravati dal proprio peso, più non potrebber reggersi, ma si strapperebbero. Piglisi, per esempio, un fil di rame di qualsivoglia grossezza e lunghezza, e fermato un de' suoi capi ad alto, si vadia aggiungendo all'altro maggior e maggior peso, sì che finalmente si strappi; e sia il peso massimo che potesse sostenere, v. g., cinquanta libbre: è manifesto che cinquanta libbre di rame, oltre al proprio peso, che sia, per esempio, un ottavo d'oncia, tirato in filo di tal grossezza, sarebbe la lunghezza massima del filo che se stesso potesse reggere. Misurisi poi quanto era lungo il filo che si strappò, e sia, v. g., un braccio: e perché pesò un ottavo d'oncia, e resse se stesso e cinquanta libbre appresso, che sono ottavi d'oncia quattro mila ottocento, diremo, tutti i fili di rame, qualunque si sia la loro grossezza, potersi reggere sino alla lunghezza di quattro mila ottocento un braccio, e non più. E così, una verga di rame potendo reggersi sino alla lunghezza di quattro mila ottocento un braccio, la resistenza che ella trova dependente dal vacuo, rispetto al restante, è tanta, quanto importa il peso d'una verga d'acqua lunga braccia diciotto e grossa quanto quella stessa di rame; e trovandosi, v. g., il rame esser nove volte più grave dell'acqua, di qualunque verga di rame la resistenza allo strapparsi, dependente dalla ragion del vacuo, importa quanto è il peso di due braccia dell'istessa verga. E con simil discorso ed operazione si potranno trovare le lunghezze delle fila o verghe di tutte le materie solide ridotte alla massima che sostener si possa, ed insieme qual parte abbia il vacuo della loro resistenza.

Sagr. Resta ora che ci dichiate in qual cosa consista il resto della resistenza, cioè qual sia il glutine o visco che ritien attaccate le parti del solido, oltre a quello che deriva dal vacuo: perché io non saprei imaginarmi qual colla sia quella che non possa esser arsa e consumata dentro una ardentissima fornace in due, tre e quattro mesi, né in dieci o in cento; dove stando tanto tempo argento oro e vetro liquefatti, cavati, poi tornano le parti loro, nel freddarsi, a riunirsi e rattaccarsi come prima. Oltre che, la medesima difficoltà che ho nell'attaccamento delle parti del vetro, l'arò io nelle parti della colla, cioè che cosa sia quella che le tiene così saldamente congiunte.

Salv. Pur poco fa vi dissi che 'l vostro demonio vi assisteva. Sono io ancora nelle medesime angustie; ed ancor io, toccando con mano come la repugnanza al vacuo è indubitabilmente quella che non permette, se non con gran violenza, la separazione delle due lastre, e più delle due gran parti della colonna di marmo o di bronzo, non so vedere come non abbia ad aver luogo ed esser parimente cagione della coerenza delle parti minori e sino delle minime ultime delle medesime materie: ed essendo che d'un effetto una sola è la vera e potissima causa, mentre io non trovo altro glutine, perché non debbo tentar di vedere se questo del vacuo, che si trova, può bastarci?

Simp. Se di già voi avete dimostrato, la resistenza del gran vacuo, nel separarsi le due gran parti di un solido, esser piccolissima in comparazion di quella che tien congiunte le particole minime, come non volete tener più che per certo, questa esser diversissima da quella?

Salv. A questo rispose il Sig. Sagredo, che pur si pagavano tutti i particolari soldati con danari raccolti da imposizioni generali di soldi e di quattrini, se bene un million d'oro non bastava a pagar tutto l'esercito. E chi sa che altri minutissimi vacui non lavorino per le minutissime particole, sì che per tutto sia dell'istessa moneta quello con che si tengono tutte le parti congiunte? Io vi dirò quello che tal ora mi è passato per l'imaginazione, e ve lo do non come verità risoluta, ma come una qual si sia fantasia, piena anco d'indigestioni, sottoponendola a più alte contemplazioni: cavatene se nulla vi è che vi gusti; il resto giudicatelo come più vi pare. Nel considerar tal volta come, andando il fuoco serpendo tra le minime particole di questo e di quel metallo, che tanto saldamente si trovano congiunte, finalmente le separa e disunisce; e come poi, partendosi il fuoco, tornano con la medesima tenacità di prima a ricongiugnersi, senza diminuirsi punto la quantità nell'oro, e pochissimo in altri metalli, anco per lungo tempo che restino distrutti; pensai che ciò potesse accadere perché le sottilissime particole del fuoco, penetrando per gli angusti pori del metallo (tra i quali, per la loro strettezza, non potessero passare i minimi dell'aria né di molti altri fluidi), col riempiere i minimi vacui tra esse fraposti liberassero le minime particole di quello dalla violenza con la quale i medesimi vacui l'una contro l'altra attraggono, proibendogli la separazione; e così, potendosi liberamente muovere, la lor massa ne divenisse fluida, e tale restasse sin che gl'ignicoli tra esse dimorassero; partendosi poi quelli e lasciando i pristini vacui, tornasse la lor solita attrazzione, ed in consequenza l'attaccamento delle parti. Ed all'istanza del Sig. Simplicio parmi che si possa rispondere, che se bene tali vacui sarebber piccolissimi, ed in consequenza ciascheduno facile ad esser superato, tuttavia l'innumerabile moltitudine innumerabilmente (per così dire) multiplica le resistenze: e quale e quanta sia la forza che da numero immenso di debolissimi momenti insieme congiunti risulta, porgacene evidentissimo argomento il veder noi un peso di milioni di libbre, sostenuto da canapi grossissimi, cedere e finalmente lasciarsi vincere e sollevare dall'assalto de gl'innumerabili atomi di acqua, li quali, o spinti dall'austro, o pur che, distesi in tenuissima nebbia, si vadano movendo per l'aria, vanno a cacciarsi tra fibra e fibra de i canapi tiratissimi, né può l'immensa forza del pendente peso vietargli l'entrata; sì che, penetrando per gli angusti meati, ingrossano le corde e per consequenza le scorciano, onde la mole gravissima a forza vien sollevata.

Sagr. Ei non è dubbio alcuno che mentre una resistenza non sia infinita, può dalla moltitudine di minimissime forze esser superata, sì che anco un numero di formiche stracicherebbe per terra una nave carica di grano; perché il senso ci mostra cotidianamente che una formica destramente porta un granello, e chiara cosa è che nella nave non sono infiniti granelli, ma compresi dentro a qualche numero, del quale se ne può prendere un altro quattro e sei volte maggiore, al quale se se ne prenderà un altro di formiche eguale, e si porranno in opera, condurranno per terra il grano e la nave ancora. È ben vero che bisognerà che il numero sia grande, come anco, per mio parere, quello de i vacui che tengono attaccati i minimi del metallo.

Salv. Ma quando bisognasse che fussero anche infiniti, l'avete voi forse per impossibile?

Sagr. No, quando quel metallo fusse una mole infinita: altrimenti...

Salv. Altrimenti che? Orsù, già che si è messo mano a i paradossi, veggiamo se in qualche maniera si potesse dimostrare, come in una continua estensione finita non repugni il potersi ritrovar infiniti vacui; e nell'istesso tempo ci verrà, se non altro, almeno arrecata una soluzione del più ammirabil problema che sia da Aristotele messo tra quelli che esso medesimo addimanda ammirandi, dico tra le questioni mecaniche; e la soluzione potrebbe esser per avventura non meno esplicante e concludente di quella che egli medesimo ne arreca, e diversa anco da quello che molto acutamente vi considera il dottissimo Monsig. di Guevara. Ma bisogna prima dichiarare una proposizione non toccata da altri, dalla quale depende lo scioglimento della questione, che poi, s'io non m'inganno, si tira dietro altre notizie nuove ed ammirande: per intelligenza di che, accuratamente descriveremo la figura.

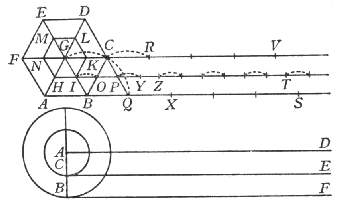
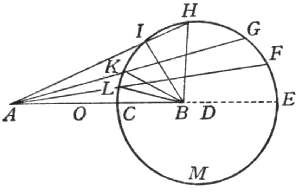
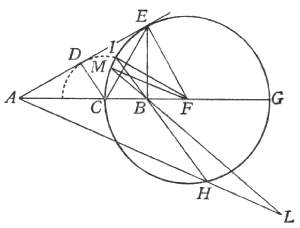
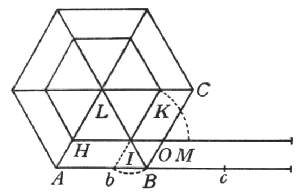
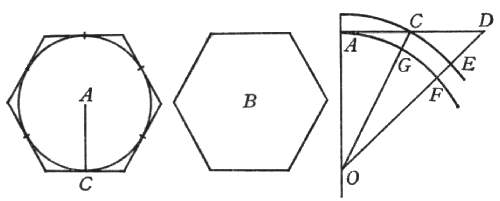
Però intendiamo un poligono equilatero ed equiangolo, di quanti lati esser si voglia, descritto intorno a questo centro G, e sia per ora un esagono ABCDEF; simile al quale, e ad esso concentrico, ne descriveremo un altro minore, quale noteremo HIKLMN: e del maggiore si prolunghi un lato AB indeterminatamente verso S, e del minore il rispondente lato HI sia verso la medesima parte similmente prodotto, segnando la linea HT parallela all'AS, e per il centro passi l'altra, alle medesime equidistante, GV. Fatto questo, intendiamo il maggior poligono rivolgersi sopra la linea AS, portando seco l'altro poligono minore. È chiaro che, stando fisso il punto B, termine del lato AB, mentre si comincia la revoluzione, l'angolo A si solleverà, e 'l punto C s'abbasserà descrivendo l'arco CQ, sì che il lato BC si adatti alla linea a se stesso eguale BQ: ma in tal conversione l'angolo I del minor poligono si eleverà sopra la linea IT, per esser la IB obliqua sopra l'AS, né prima tornerà il punto I su la parallela IT, se non quando il punto C sarà pervenuto in Q; allora l'I sarà caduto in O, dopo aver descritto l'arco IO fuori della linea HT, ed allora il lato IK sarà passato in OP: ma il centro G tra tanto sempre averà caminato fuori della linea GV, su la quale non sarà tornato se non dopo aver descritto l'arco GC. Fatto questo primo passo, il poligono maggiore sarà trasferito a posare co 'l lato BC su la linea BQ, il lato IK del minore sopra la linea OP, avendo saltato tutta la parte IO senza toccarla, e 'l centro G pervenuto in C, facendo tutto il suo corso fuori della parallela GV, e finalmente tutta la figura si sarà rimessa in un posto simile al primo: sì che continuandosi la revoluzione e venendo al secondo passo, il lato del maggior poligono CD si adatterà alla parte QX, il KL del minore (avendo prima saltato l'arco PY) caderà in YZ, ed il centro, procedendo sempre fuori della GV, in essa caderà solamente in R, dopo il gran salto CR: ed in ultimo, finita una intera conversione, il maggior poligono avrà calcate sopra la sua AS sei linee eguali al suo perimetro, senza veruna interposizione; il poligono minore arà parimente impresse sei linee eguali all'ambito suo, ma discontinuate dall'interposizione de' cinque archi, sotto i quali restano le corde, parti della parallela HT, non tocche dal poligono; e finalmente il centro G non è convenuto mai con la parallela GV, salvo che in sei punti. Di qui potete comprendere come lo spazio passato dal minor poligono è quasi eguale al passato del maggiore, cioè la linea HT alla AS, della quale è solamente minore quanto è la corda d'uno di questi archi, intendendo però la linea HT insieme con li spazii de i cinque archi. Ora questo, che vi ho esposto e dichiarato nell'esempio di questi essagoni, vorrei che intendeste accadere di tutti gli altri poligoni, di quanti lati esser si voglino, purché siano simili, concentrici e congiunti, e che alla conversion del maggiore s'intenda rigirarsi anco l'altro, quanto si voglia minore; che intendeste, dico, le linee da essi passate esser prossimamente eguali, computando nello spazio passato dal minore gl'intervalli sotto gli archetti, non tocchi da parte veruna del perimetro di esso minor poligono. Passa dunque il gran poligono di mille lati, e misura consequentemente, una linea retta eguale al suo ambito; e nell'istesso tempo il piccolo passa una prossimamente egual linea, ma interrottamente composta di mille particelle eguali a i suoi mille lati con l'interposizione di mille spazii vacui, che tali possiamo chiamargli in relazione alle mille lineette toccate da i lati del poligono: ed il detto sin qui non ha veruna difficoltà o dubitazione. Ma ditemi: se intorno a un centro, qual sia, v. g., questo punto A, noi descriveremo due cerchi concentrici ed insieme uniti, e che da i punti C, B de i lor semidiametri siano tirate le tangenti CE, BF, e ad esse per il centro A la parallela AD, intendendo girato il cerchio maggiore sopra la linea BF (posta eguale alla di lui circonferenza, come parimente le altre due CE, AD), compita che abbia una revoluzione, che averà fatto il minor cerchio, e che il centro? Questo sicuramente averà scorsa e toccata tutta la linea AD, e la circonferenza di quello averà con li suoi toccamenti misurata tutta la CE, facendo l'istesso che fecero i poligoni di sopra: in questo solamente differenti, che la linea HT non fu tocca in tutte le sue parti del perimetro del minor poligono, ma ne furon lasciate tante intatte, con l'interposizione de' vacui saltati, quante furon le parti tocche da i lati; ma qui ne i cerchi mai non si separa la circonferenza del minor cerchio della linea CE, sì che alcuna sua parte non venga tocca, né mai quello che tocca della circonferenza è manco del toccato nella retta. Or come dunque può senza salti scorrere il cerchio minore una linea tanto maggiore della sua circonferenza?

Sagr. Andava pensando se si potesse dire, che sì come il centro del cerchio, esso solo, stracicato copra AD, la tocca tutta, essendo anco un punto solo, così potessero i punti della circonferenza minore, tirati dal moto della maggiore, andare strascicandosi per qualche particella della linea CE.

Salv. Questo non può essere, per due ragioni. Prima, perché non sarebbe maggior ragione che alcuno de i toccamenti simili al C andassero stracicando per qualche parte della linea CE, ed altri no; e quando questo fusse, essendo tali toccamenti (perché son punti) infiniti, gli strascichi sopra la CE sarebbero infiniti, ed essendo quanti, farebbero una linea infinita; ma la CE è finita. L'altra ragione è, che mutando il cerchio grande, nella sua conversione, continuamente contatto, non può non mutarlo parimente il minor cerchio, non si potendo da altro punto che dal punto B tirare una linea retta sino al centro A e che passasse per il punto C; sì che mutando contatto la circonferenza grande, lo muta ancora la piccola, né punto alcuno della piccola tocca più d'un punto della sua retta CE. Oltre che, anco nella conversione de i poligoni nissun punto del perimetro del minore si adattava a più d'un punto della linea che dal medesimo perimetro veniva misurata; come si può facilmente intendere considerando la linea IK esser parallela alla BC, onde sin che la BC non si schiaccia sopra la BQ, la IK resta sollevata sopra la IP, né prima la calca se non nel medesimo instante che la BC si unisce con la BQ, ed allora tutta insieme la IK si unisce con la OP, e poi immediatamente se gli eleva sopra.

Sagr. Il negozio è veramente molto intrigato, né a me sovviene scioglimento alcuno: però diteci quello che a voi sovviene.

Salv. Io ricorrerei alla considerazione de i poligoni sopra considerati, l'effetto de i quali è intelligibile e di già compreso: e direi, che sì come ne i poligoni di cento mila lati alla linea passata e misurata dal perimetro del maggiore, cioè da i cento mila suoi lati continuamente distesi, è eguale la misurata da i cento mila lati del minore, ma con l'interposizione di cento mila spazii vacui traposti; così direi, ne i cerchi (che son poligoni di lati infiniti) la linea passata da gl'infiniti lati del cerchio grande, continuamente disposti, esser pareggiata in lunghezza dalla linea passata da gl'infiniti lati del minore, ma da questi con l'interposizion d'altrettanti vacui tra essi; e sì come i lati non son quanti, ma bene infiniti, così gl'interposti vacui non son quanti, ma infiniti: quelli, cioè, infiniti punti tutti pieni; e questi, infiniti punti parte pieni e parte vacui. E qui voglio che notiate, come risolvendo e dividendo una linea in parti quante, e per consequenza numerate, non è possibile disporle in una estensione maggiore di quella che occupavan mentre stavano continuate e congiunte senza l'interposizione d'altrettanti spazii vacui; ma imaginandola risoluta in parti non quante, cioè ne' suoi infiniti indivisibili, la possiamo concepire distratta in immenso senza l'interposizione di spazii quanti vacui, ma sì bene d'infiniti indivisibili vacui. E questo, che si dice delle semplici linee, s'intenderà detto delle superficie e de' corpi solidi, considerandogli composti di infiniti atomi non quanti: che mentre gli vorremo dividere in parti quante, non è dubbio che non potremo disporle in spazii più ampli del primo occupato dal solido se non con l'interposizione di spazii quanti vacui, vacui, dico, almeno della materia del solido; ma se intenderemo l'altissima ed ultima resoluzione fatta ne i primi componenti non quanti ed infiniti potremo concepire tali componenti distratti in spazio immenso senza l'interposizione di spazii quanti vacui, ma solamente di vacui infiniti non quanti: ed in questa guisa non repugna distrarsi, v. g., un piccolo globetto d'oro in uno spazio grandissimo senza ammettere spazii quanti vacui; tutta volta però che ammettiamo, l'oro esser composto di infiniti indivisibili.

Simp. Parmi che voi caminiate alla via di quei vacui disseminati di certo filosofo antico.

Salv. Ma però voi non soggiugnete «il quale negava la Providenza divina», come in certo simil proposito, assai poco a proposito, soggiunse un tale antagonista del nostro Accademico.

Simp. Veddi bene, e non senza stomaco, il livore del mal affetto contradittore: ma io non solamente per termine di buona creanza non toccherei simili tasti, ma perché so quanto sono discordi dalla mente ben temperata e bene organizzata di V. S., non solo religiosa e pia, ma cattolica e santa. Ma ritornando su 'l proposito, molte difficoltà sento nascermi da gli auti discorsi, dalle quali veramente io non saprei liberarmi. E per una mi si para avanti questa, che se le circonferenze de i due cerchi sono eguali alle due rette CE, BF, questa continuamente presa, e quella con l'interposizione d'infiniti punti vacui, l'AD descritta dal centro, che è un punto solo, in qual maniera si potrà chiamare ad esso eguale, contenendone infiniti? In oltre, quel comporre la linea di punti, il divisibile di indivisibili, il quanto di non quanti, mi paiono scogli assai duri da passargli e l'istesso dover ammettere il vacuo, tanto concludentemente reprovato da Aristotele, non manca delle medesime difficoltà.

Salv. Ci sono veramente coteste, e dell'altre: ma ricordiamoci che siamo tra gl'infiniti e gl'indivisibili, quelli incomprensibili dal nostro intelletto finito per la lor grandezza, e questi per la lor piccolezza. Con tutto ciò veggiamo che l'umano discorso non vuol rimanersi dall'aggirarsegli attorno; dal che pigliando io ancora qualche libertà, produrrei alcuna mia fantasticheria, se non concludente necessariamente, almeno, per la novità, apportatrice di qualche maraviglia. Ma forse il divertir tanto lungamente dal cominciato cammino potrebbe parervi importuno, e però poco grato.

Sagr. Di grazia, godiamo del benefizio e privilegio che s'ha dal parlar con i vivi e tra gli amici, e più di cose arbitrarie e non necessarie, differente dal trattar co' i libri morti, li quali ti eccitano mille dubbi e nissuno te ne risolvono. Fateci dunque partecipi di quelle considerazioni che il corso de i nostri ragionamenti vi suggerisce, ché non ci mancherà tempo, mercé dell'esser noi disobbligati da funzioni necessarie, di continuar e risolvere l'altre materie intraprese; ed in particolare i dubbii toccati dal Sig. Simplicio non si trapassino in tutti i modi.

Salv. Così si faccia, poiché tale è il vostro gusto: e cominciando dal primo, che fu come si possa mai capire che un sol punto sia eguale ad una linea, vedendo di non ci poter far altro per ora, procurerò di quietare o almeno temperare una improbabilità con un'altra simile o maggiore, come talvolta una maraviglia si attutisce con un miracolo. E questo sarà col mostrarvi, due superficie eguali, ed insieme due corpi pur eguali e sopra le medesime dette superficie, come basi loro, collocati, andarsi continuamente ed egualmente, e queste e quelli, nel medesimo tempo diminuendo, restando sempre tra di loro eguali i loro residui, e finalmente andare, sì le superficie come i solidi, a terminare le lor perpetue egualità precedenti, l'uno de i solidi con l'una delle superficie in una lunghissima linea, e l'altro solido con l'altra superficie in un sol punto, cioè, questi in un sol punto, e quelli in infiniti.

Sagr. Ammirabil proposta veramente mi par cotesta; però sentiamone l'esplicazione e la dimostrazione.

Salv. È necessario farne la figura, perché la prova è pura geometrica.

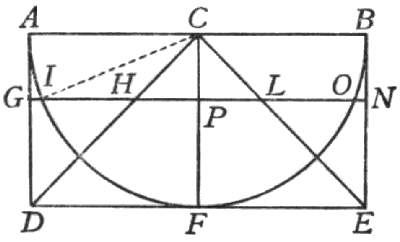
Per tanto intendasi il mezzo cerchio AFB, il cui centro C, ed intorno ad esso il parallellogrammo rettangolo ADEB, e dal centro a i punti D, E siano tirate le rette linee CD, CE; figurandoci poi il semidiametro CF, perpendicolare a una delle due AB, DE, immobile, intendiamo intorno a quello girarsi tutta questa figura: è manifesto che dal rettangolo ADEB verrà descritto un cilindro, dal semicircolo AFB una mezza sfera, e dal triangolo CDE un cono. Inteso questo, voglio che ci immaginiamo esser levato via l'emisferio, lasciando però il cono e quello che rimarrà del cilindro, il quale, dalla figura che riterrà simile a una scodella, chiameremo pure scodella: della quale e del cono prima dimostreremo che sono eguali; e poi, un piano tirato parallelo al cerchio che è base della scodella, il cui diametro è la linea DE e centro F, dimostreremo, tal piano, che passasse, v. g., per la linea GN, segando la scodella ne i punti G, I, O, N, ed il cono ne' punti H, L, tagliare la parte del cono CHL eguale sempre alla parte della scodella, il cui profilo ci rappresentano i triangoli GAI, BON; e di più si proverà, la base ancora del medesimo cono, cioè il cerchio il cui diametro HL, esser eguale a quella circolar superficie che è base della parte della scodella, che è come se dicessimo un nastro di larghezza quanta è la linea GI (notate intanto che cosa sono le definizioni de i matematici, che sono una imposizion di nomi, o vogliam dire abbreviazioni di parlare, ordinate ed introdotte per levar lo stento tedioso che voi ed io sentiamo di presente per non aver convenuto insieme di chiamar, v. g., questa superficie, nastro circolare, e quel solido acutissimo della scodella rasoio rotondo): or comunque vi piaccia chiamargli, bastivi intendere che il piano prodotto per qualsivoglia distanza, pur che sia parallelo alla base, cioè al cerchio il cui diametro DE, taglia sempre i due solidi, cioè la parte del cono CHL e la superior parte della scodella, eguali tra di loro, e parimente le due superficie basi di tali solidi, cioè il detto nastro e 'l cerchio HL, pur tra loro eguali. Del che ne segue la maraviglia accennata: cioè, che se intenderemo il segante piano successivamente inalzato verso la linea AB, sempre le parti de i solidi tagliate sono eguali, come anco le superficie, che son basi loro, pur sempre sono eguali; e finalmente, alzando e alzando tanto li due solidi (sempre eguali) quanto le lor basi (superficie pur sempre eguali), vanno a terminare l'una coppia di loro in una circonferenza di un cerchio, e l'altra in un sol punto, ché tali sono l'orlo supremo della scodella e la cuspide del cono. Or mentre che nella diminuzione de i due solidi si va, sino all'ultimo, mantenendo sempre tra essi la egualità, ben par conveniente il dire che gli altissimi ed ultimi termini di tali menomamenti restino tra di loro eguali, e non l'uno infinitamente maggior dell'altro: par dunque che la circonferenza di un cerchio immenso possa chiamarsi eguale a un sol punto. E questo che accade ne i solidi, accade parimente nelle superficie, basi loro, che esse ancora, conservando nella comune diminuzione sempre la egualità, vanno in fine ad incontrare, nel momento della loro ultima diminuzione, quella per suo termine la circonferenza di un cerchio, e questa un sol punto; li quali perché non si devon chiamare eguali, se sono le ultime reliquie e vestigie lasciate da grandezze eguali? E notate appresso, che quando ben fussero tali vasi capaci de gl'immensi emisferii celesti, tanto gli orli loro supremi e le punte de i contenuti coni, servando sempre tra loro l'egualità, andrebbero a terminare, quelli in circonferenze eguali a quelle de i cerchi massimi de gli orbi celesti, e questi in semplici punti. Onde, conforme a quello che tali specolazioni ne persuadono, anco tutte le circonferenze de' cerchi quanto si voglia diseguali, posson chiamarsi tra loro eguali, e ciascheduna eguale a un punto solo.

Sagr. La specolazione mi par tanto gentile e peregrina, che io, quando ben potessi, non me gli vorrei opporre, ché mi parrebbe un mezzo sacrilegio lacerar sì bella struttura, calpestandola con qualche pedantesco affronto: però per intera sodisfazione recateci pur la prova, che dite geometrica, del mantenersi sempre l'egualità tra quei solidi e quelle basi loro, che penso che non possa esser se non molto arguta, essendo così sottile la filosofica meditazione che da tal conclusione depende.

Salv. La dimostrazione è anco breve e facile. Ripigliamo la segnata figura, nella quale, per esser l'angolo IPC retto, il quadrato del semidiametro IC è eguale alli due quadrati de i lati IP, PC: ma il semidiametro IC è eguale alla AC, e questa alla GP, e la CP è eguale alla PH; adunque il quadrato della linea GP è eguale alli due quadrati delle IP, PH e 'l quadruplo e i quadrupli, cioè il quadrato del diametro GN è eguale alli due quadrati IO, HL: e perché i cerchi son tra loro come i quadrati de' lor diametri, il cerchio il cui diametro GN sarà eguale alli due cerchi i cui diametri IO, HL, e tolto via il comune cerchio il cui diametro IO, il residuo del cerchio GN sarà eguale al cerchio il cui diametro è HL. E questo è quanto alla prima parte: quanto poi all'altra parte, lasceremo per ora la dimostrazione, sì perché, volendola noi vedere, la troveremo nella duodecima proposizione del libro secondo De centro gravitatis solidorum posta dal Sig. Luca Valerio, nuovo Archimede dell'età nostra, il quale per un altro suo proposito se ne servì, sì perché nel caso nostro basta l'aver veduto come le superficie già dichiarate siano sempre eguali, e che, diminuendosi sempre egualmente, vadano a terminare l'una in un sol punto e l'altra nella circonferenza d'un cerchio, maggiore anco di qualsivoglia grandissimo, perché in questa consequenza sola versa la nostra maraviglia.

Sagr. Ingegnosa la dimostrazione, quanto mirabile la reflessione fattavi sopra. Or sentiamo qualche cosa circa l'altra difficoltà promossa dal Sig. Simplicio, se però avete alcuna particolarità da dirvi sopra, che crederei che non potesse essere, essendo una controversia stata tanto esagitata.

Salv. Avrò qualche mio pensiero particolare, replicando prima quel che poco fa dissi, cioè che l'infinito è per sé solo da noi incomprensibile, come anco gl'indivisibili; or pensate quel che saranno congiunti insieme: e pur se vogliamo compor la linea di punti indivisibili, bisogna fargli infiniti; e così conviene apprender nel medesimo tempo l'infinito e l'indivisibile. Le cose che in più volte mi son passate per la mente in tal proposito, son molte, parte delle quali, e forse le più considerabili, potrebb'esser che, così improvvisamente, non mi sovvenissero; ma nel progresso del ragionamento potrà accadere che, destando io a voi, ed in particolare al Sig. Simplicio, obbiezzioni e difficoltà, essi all'incontro mi facessero ricordar di quello che senza tale eccitamento restasse dormendo nella fantasia: e però con la solita libertà sia lecito produrre in mezzo i nostri umani capricci, ché tali meritamente possiamo nominargli in comparazione delle dottrine sopranaturali, sole vere e sicure determinatrici delle nostre controversie, e scorte inerranti ne i nostri oscuri e dubbii sentieri o più tosto labirinti.
Tra le prime istanze che si sogliono produrre contro a quelli che compongono il continuo d'indivisibili, suol esser quella che uno indivisibile aggiunto a un altro indivisibile non produce cosa divisibile, perché, se ciò fusse, ne seguirebbe che anco l'indivisibile fusse divisibile; perché quando due indivisibili, come, per esempio, due punti congiunti facessero una quantità, qual sarebbe una linea divisibile, molto più sarebbe tale una composta di tre, di cinque, di sette e di altre moltitudini dispari; le quali linee essendo poi segabili in due parti eguali, rendon segabile quell'indivisibile che nel mezzo era collocato. In questa ed altre obbiezzioni di questo genere si dà sodisfazione alla parte con dirgli, che non solamente due indivisibili, ma né dieci, né cento, né mille non compongono una grandezza divisibile e quanta, ma sì bene infiniti.

Simp. Qui nasce subito il dubbio, che mi pare insolubile: ed è, che sendo noi sicuri trovarsi linee una maggior dell'altra, tutta volta che amendue contenghino punti infiniti, bisogna confessare trovarsi nel medesimo genere una cosa maggior dell'infinito, perché la infinità de i punti della linea maggiore eccederà l'infinità de i punti della minore. Ora questo darsi un infinito maggior dell'infinito mi par concetto da non poter esser capito in verun modo.

Salv. Queste son di quelle difficoltà che derivano dal discorrer che noi facciamo col nostro intelletto finito intorno a gl'infiniti, dandogli quelli attributi che noi diamo alle cose finite e terminate; il che penso che sia inconveniente, perché stimo che questi attributi di maggioranza, minorità ed egualità non convenghino a gl'infiniti, de i quali non si può dire, uno esser maggiore o minore o eguale all'altro. Per prova di che già mi sovvenne un sì fatto discorso, il quale per più chiara esplicazione proporrò per interrogazioni al Sig. Simplicio, che ha mossa la difficoltà.
Io suppongo che voi benissimo sappiate quali sono i numeri quadrati, e quali i non quadrati.

Simp. So benissimo che il numero quadrato è quello che nasce dalla moltiplicazione d'un altro numero in se medesimo: e così il quattro, il nove, etc., son numeri quadrati, nascendo quello dal dua, e questo dal tre, in se medesimi moltiplicati.

Salv. Benissimo: e sapete ancora, che sì come i prodotti si dimandano quadrati, i producenti, cioè quelli che si multiplicano, si chiamano lati o radici; gli altri poi, che non nascono da numeri multiplicati in se stessi, non sono altrimenti quadrati. Onde se io dirò, i numeri tutti, comprendendo i quadrati e i non quadrati, esser più che i quadrati soli, dirò proposizione verissima: non è così?

Simp. Non si può dir altrimenti.

Salv. Interrogando io di poi, quanti siano i numeri quadrati, si può con verità rispondere, loro esser tanti quante sono le proprie radici, avvenga che ogni quadrato ha la sua radice, ogni radice il suo quadrato, né quadrato alcuno ha più d'una sola radice, né radice alcuna più d'un quadrato solo.

Simp. Così sta.

Salv. Ma se io domanderò, quante siano le radici, non si può negare che elle non siano quante tutti i numeri, poiché non vi è numero alcuno che non sia radice di qualche quadrato; e stante questo, converrà dire che i numeri quadrati siano quanti tutti i numeri, poiché tanti sono quante le lor radici, e radici son tutti i numeri: e pur da principio dicemmo, tutti i numeri esser assai più che tutti i quadrati, essendo la maggior parte non quadrati. E pur tuttavia si va la moltitudine de i quadrati sempre con maggior proporzione diminuendo, quanto a maggior numeri si trapassa; perché sino a cento vi sono dieci quadrati, che è quanto dire la decima parte esser quadrati; in dieci mila solo la centesima parte sono quadrati, in un millione solo la millesima: e pur nel numero infinito, se concepir lo potessimo, bisognerebbe dire, tanti essere i quadrati quanti tutti i numeri insieme.

Sagr. Che dunque si ha da determinare in questa occasione?

Salv. Io non veggo che ad altra decisione si possa venire, che a dire, infiniti essere tutti i numeri, infiniti i quadrati, infinite le loro radici, né la moltitudine de' quadrati esser minore di quella di tutti i numeri, né questa maggior di quella, ed in ultima conclusione, gli attributi di eguale maggiore e minore non aver luogo ne gl'infiniti, ma solo nelle quantità terminate. E però quando il Sig. Simplicio mi propone più linee diseguali, e mi domanda come possa essere che nelle maggiori non siano più punti che nelle minori, io gli rispondo che non ve ne sono né più né manco né altrettanti, ma in ciascheduna infiniti: o veramente se io gli rispondessi, i punti nell'una esser quanti sono i numeri quadrati, in un'altra maggiore quanti tutti i numeri, in quella piccolina quanti sono i numeri cubi, non potrei io avergli dato sodisfazione col porne più in una che nell'altra, e pure in ciascheduna infiniti? E questo è quanto alla prima difficoltà.

Sagr. Fermate in grazia, e concedetemi che io aggiunga al detto sin qui un pensiero, che pur ora mi giugne: e questo è, che, stanti le cose dette sin qui, parmi che non solamente non si possa dire, un infinito esser maggiore d'un altro infinito, ma né anco che e' sia maggior d'un finito, perché se 'l numero infinito fusse maggiore, v. g., del millione, ne seguirebbe, che passando dal millione ad altri e ad altri continuamente maggiori, si camminasse verso l'infinito; il che non è: anzi, per l'opposito a quanto maggiori numeri facciamo passaggio, tanto più ci discostiamo dal numero infinito; perché ne i numeri, quanto più si pigliano grandi, sempre più e più rari sono i numeri quadrati in esso contenuti; ma nel numero infinito i quadrati non possono esser manco che tutti i numeri, come pur ora si è concluso; adunque l'andar verso numeri sempre maggiori e maggiori è un discostarsi dal numero infinito.

Salv. E così dal vostro ingegnoso discorso si conclude, gli attributi di maggiore minore o eguale non aver luogo non solamente tra gl'infiniti, ma né anco tra gl'infiniti e i finiti.

Passo ora ad un'altra considerazione, ed è, che stante che la linea ed ogni continuo sian divisibili in sempre divisibili, non veggo come si possa sfuggire, la composizione essere di infiniti indivisibili, perché una divisione e subdivisione che si possa proseguir perpetuamente, suppone che le parti siano infinite, perché altramente la subdivisione sarebbe terminabile; e l'esser le parti infinite si tira in consequenza l'esser non quante, perché quanti infiniti fanno un'estensione infinita: e così abbiamo il continuo composto d'infiniti indivisibili.

Simp. Ma se noi possiamo proseguir sempre la divisione in parti quante, che necessità abbiamo noi di dover, per tal rispetto, introdur le non quante?

Salv. L'istesso poter proseguir perpetuamente la divisione in parti quante, induce la necessità della composizione di infiniti non quanti. Imperò che, venendo più alle strette, io vi domando che resolutamente mi diciate, se le parti quante nel continuo, per vostro credere, son finite o infinite?

Simp. Io vi rispondo, essere infinite e finite: infinite, in potenza; e finite, in atto: infinite in potenza, cioè innanzi alla divisione; ma finite in atto, cioè dopo che son divise; perché le parti non s'intendono attualmente esser nel suo tutto, se non dopo esser divise o almeno segnate; altramente si dicono esservi in potenza.

Salv. Sì che una linea lunga, v. g., venti palmi non si dice contener venti linee di un palmo l'una attualmente, se non dopo la divisione in venti parti eguali; ma per avanti si dice contenerle solamente in potenza. Or sia come vi piace; e ditemi se, fatta l'attual divisione di tali parti, quel primo tutto cresce o diminuisce, o pur resta della medesima grandezza?

Simp. Non cresce, né scema.

Salv. Così credo io ancora. Adunque le parti quante nel continuo, o vi siano in atto o vi siano in potenza, non fanno la sua quantità maggiore né minore: ma chiara cosa è, che parti quante attualmente contenute nel lor tutto, se sono infinite, lo fanno di grandezza infinita: adunque parti quante, benché in potenza solamente, infinite, non possono esser contenute se non in una grandezza infinita; adunque nella finita parti quante infinite, né in atto né in potenza possono esser contenute.

Sagr. Come dunque potrà esser vero che il continuo possa incessabilmente dividersi in parti capaci sempre di nuova divisione?

Salv. Par che quella distinzione d'atto e di potenza vi renda fattibile per un verso quel che per un altro sarebbe impossibile. Ma io vedrò d'aggiustar meglio queste partite con fare un altro computo; ed al quesito che domanda se le parti quante nel continuo terminato sian finite o infinite, risponderò tutto l'opposto di quel che rispose dianzi il Sig. Simplicio, cioè non esser né finite né infinite.

Simp. Ciò non arei saputo mai risponder io, non pensando che si trovasse termine alcuno mezzano tra 'l finito e l'infinito, sì che la divisione o distinzione che pone, una cosa o esser finita o infinita, fusse manchevole e difettosa.

Salv. A me par ch'ella sia. E parlando delle quantità discrete, parmi che tra le finite e l'infinite ci sia un terzo medio termine, che è il rispondere ad ogni segnato numero; sì che, domandato, nel presente proposito, se le parti quante nel continuo siano finite o infinite, la più congrua risposta sia il dire, non esser né finite né infinite, ma tante che rispondono ad ogni segnato numero: per il che fare è necessario che elle non siano comprese dentro a un limitato numero, perché non risponderebbono ad un maggiore; ma né anco è necessario che elle siano infinite, perché niuno assegnato numero è infinito: e così ad arbitrio del domandante una proposta linea gliela potremo assegnare segata in cento parti quante, e in mille e in cento mila, conforme a qual numero più gli piacerà; ma divisa in infinite, questo non già. Concedo dunque a i Signori filosofi che il continuo contiene quante parti quante piace loro, e gli ammetto che le contenga in atto o in potenza, a lor gusto e beneplacito; ma gli soggiungo poi, che nel modo che in una linea di dieci canne si contengono dieci linee d'una canna l'una, e quaranta d'un braccio l'una, e ottanta di mezzo braccio, etc., così contiene ella punti infiniti: chiamateli poi in atto o in potenza, come più vi piace, ché io, Sig. Simplicio, in questo particolare mi rimetto al vostro arbitrio e giudizio.

Simp. Io non posso non laudare il vostro discorso: ma ho gran paura che questa parità dell'esser contenuti i punti come le parti quante non corra con intera puntualità, né che a voi sarà così agevole il dividere la proposta linea in infiniti punti, come a quei filosofi in dieci canne o in quaranta braccia: anzi ho per impossibile del tutto il ridurr'ad effetto tal divisione, sì che questa sarà una di quelle potenze che mai non si riducono in atto.

Salv. L'esser una cosa fattibile se non con fatica o diligenza, o in gran lunghezza di tempo, non la rende impossibile, perché penso che voi altresì non così agevolmente vi sbrighereste da una divisione da farsi d'una linea in mille parti, e molto meno dovendo dividerla in 937 o altro gran numero primo. Ma se questa, che voi per avventura stimate divisione impossibile, io ve la riducessi a così spedita come se altri la dovesse segare in quaranta, vi contentereste voi di ammetterla più placidamente nella nostra conversazione?

Simp. Io gusto del vostro trattar, come fate talora con qualche piacevolezza; ed al quesito vi rispondo, che la facilità mi parrebbe grande più che a bastanza, quando il risolverla in punti non fusse più laborioso che il dividerla in mille parti.

Salv. Qui voglio dirvi cosa che forse vi farà maravigliare, in proposito del volere o poter risolver la linea ne' suoi infiniti tenendo quell'ordine che altri tiene nel dividerla in quaranta, sessanta o cento parti, cioè con l'andarla dividendo in due e poi in quattro etc.: col qual ordine chi credesse di trovare i suoi infiniti punti, s'ingannerebbe indigrosso, perché con tal progresso né men alla division di tutte le parti quante si perverrebbe in eterno; ma de gli indivisibili tanto è lontano il poter giugner per cotal strada al cercato termine, che più tosto altri se ne discosta, e mentre pensa, col continuar la divisione e col multiplicar la moltitudine delle parti, di avvicinarsi alla infinità, credo che sempre più se n'allontani: e la mia ragione è questa. Nel discorso auto poco fa concludemmo, che nel numero infinito bisognava che tanti fussero i quadrati o i cubi quanti tutti i numeri, poiché e questi e quelli tanti sono quante le radici loro, e radici son tutti i numeri. Vedemmo appresso, che quanto maggiori numeri si pigliavano, tanto più radi si trovavano in essi i lor quadrati, e più radi ancora i lor cubi: adunque è manifesto, che a quanto maggiori numeri noi trapassiamo, tanto più ci discostiamo dal numero infinito; dal che ne séguita che, tornando in dietro (poiché tal progresso sempre più ci allontana dal termine ricercato), se numero alcuno può dirsi infinito, questo sia l'unità. E veramente in essa son quelle condizioni e necessarii requisiti del numero infinito, dico del contener in sé tanti quadrati quanti cubi e quanti tutti i numeri.

Simp. Io non capisco bene come si deva intender questo negozio.

Salv. Il negozio non ha in sé dubbio veruno, perché l'unità è quadrato, è cubo, è quadrato quadrato e tutte le altre dignità, né vi è particolarità veruna essenziale a i quadrati, a i cubi, etc., che non convenga all'uno: come, v. g., proprietà di due numeri quadrati è l'aver tra di loro un numero medio proporzionale; pigliate qualsivoglia numero quadrato per l'uno de' termini e per l'altro l'unità, sempre ci troverete un numero medio proporzionale. Siano due numeri quadrati 9 e 4: eccovi, tra 'l 9 e l'uno, medio proporzionale il 3; fra 'l 4 e l'uno media il 2; e tra i due quadrati 9 e 4 vi è il 6 in mezzo. Proprietà de i cubi è l'esser tra essi necessariamente due numeri medii proporzionali: ponete 8 e 27, già tra loro son medii 12 e 18; e tra l'uno e l'8 mediano il 2 e 'l 4; e tra l'uno e 'l 27, il 3 e 'l 9. Concludiamo per tanto, non ci essere altro numero infinito che l'unità. E queste sono delle maraviglie che superano la capacità della nostra immaginazione, e che devriano farci accorti quanto gravemente si erri mentre altri voglia discorrere intorno a gl'infiniti con quei medesimi attributi che noi usiamo intorno a i finiti, le nature de i quali non hanno veruna convenienza tra di loro.

In proposito di che non voglio tacervi un mirabile accidente che pur ora mi sovviene, esplicante l'infinita differenza, anzi repugnanza e contrarietà di natura, che incontrerebbe una quantità terminata nel trapassar all'infinita.

Segniamo questa linea retta AB di qualsivoglia lunghezza; e preso in lei qualsivoglia punto C, che in parti diseguali la divida, dico che partendosi coppie di linee da i termini A, B, che, ritenendo fra di loro la medesima proporzione che hanno le parti AC, BC, vadiano a concorrere insieme, i punti de i lor concorsi cadranno tutti nella circonferenza di un medesimo cerchio: come, per esempio, partendosi le AL, BL da i punti A, B, ed avendo tra di loro la medesima proporzione che hanno le parti AC, BC, ed andando a concorrere nel punto L, e ritenendo l'istessa proporzione altre due AK, BK, concorrendo in K, altre AI, BI, AH, HB, AG, GB, AF, FB, AE, EB, dico che i punti de i concorsi L, K, I, H, G, F, E cascano tutti nella circonferenza di un istesso cerchio; talché se ci immagineremo, il punto C muoversi continuamente con tal legge, che le linee da esso prodotte sino a i termini fissi A, B mantenghino sempre la proporzione medesima che hanno le prime parti AC, CB, tal punto C descriverà la circonferenza d'un cerchio, come appresso vi dimostrerò; ed il cerchio in cotal modo descritto sarà sempre maggiore e maggiore infinitamente, secondo che il punto C sarà preso più vicino al punto di mezzo, che sia O, e minore sarà quel cerchio che dal punto più vicino all'estremità B sarà descritto; in maniera che da i punti infiniti che pigliar si possono nella linea OB si descriveranno cerchi (movendogli con l'esplicata legge) di qualsivoglia grandezza, minori della luce dell'occhio d'una pulce, e maggiori dell'equinoziale del primo mobile. Ora, se alzandosi qualsivoglia de i punti compresi tra i termini O, B, da tutti si descrivono cerchi, e immensi da i punti prossimi all'O, alzando l'istesso O e continuando di muoverlo con l'osservanza dell'istesso decreto, cioè che le linee da esso prodotte sino a i termini A, B ritenghino la proporzione che hanno le prime linee AO, OB, che linea verrà segnata? Segnerassi la circonferenza d'un cerchio, ma d'un cerchio maggiore di tutti gli altri massimi, di un cerchio, dunque, infinito; ma si segna anco una linea retta e perpendicolare sopra la BA, eretta dal punto O e prodotta in infinito senza mai tornare a riunire il suo termine ultimo col suo primo, come ben tornavano l'altre: imperò che la segnata per il moto limitato del punto C, dopo segnato il mezzo cerchio superiore CHE, continuava di segnare l'inferiore EMC, riunendo insieme i suoi estremi termini nel punto C; ma il punto O, mossosi per segnar, come tutti gli altri della linea AB (perché i punti presi nell'altra parte OA descriveranno essi ancora i lor cerchi, ed i massimi i punti prossimi all'O), il suo cerchio, per farlo massimo di tutti, e per conseguenza infinito, non può più ritornare nel suo primo termine, ed in somma descrive una linea retta infinita per circonferenza del suo infinito cerchio. Considerate ora qual differenza sia da un cerchio finito a un infinito, poiché questo muta talmente l'essere, che totalmente perde l'essere e il poter essere: ché già ben chiaramente comprendiamo, non si poter dare un cerchio infinito; il che si tira poi in consequenza, né meno poter essere una sfera infinita, né altro qualsivoglia corpo o superficie figurata e infinita. Or che diremo di cotali metamorfosi nel passar dal finito all'infinito? e perché doviamo sentir repugnanza maggiore, mentre, cercando l'infinito ne i numeri, andiamo a concluderlo nell'uno? e mentre che rompendo un solido in molte parti e seguitando di ridurlo in minutissima polvere, risoluto che si fusse ne gl'infiniti suoi atomi non più divisibili, perché non potremo dire, quello esser ritornato in un solo continuo, ma forse fluido come l'acqua o 'l mercurio o 'l medesimo metallo liquefatto? e non vediamo noi, le pietre liquefarsi in vetro, ed il vetro medesimo, co 'l molto fuoco, farsi fluido più che l'acqua?

Sagr. Doviamo dunque credere, i fluidi esser tali, perché sono risoluti ne i primi infiniti indivisibili, suoi componenti?

Salv. Io non so trovar miglior ripiego per risolver alcune sensate apparenze, tra le quali una è questa. Mentre io piglio un corpo duro, o sia pietra o metallo, e che con martello o sottilissima lima lo vo al possibile dividendo in minutissima ed impalpabile polvere, chiara cosa è che i suoi minimi, ancor che per la lor piccolezza siano impercettibili a uno a uno dalla nostra vista e dal tatto, tuttavia son eglino ancor quanti, figurati e numerabili: e di essi accade che, accumulati insieme, si sostengono ammucchiati; e scavati sino a certo segno, resta la cavità, senza che le parti d'intorno scorrano a riempirla; agitati e commossi, subito si fermano tantosto che il motore esterno gli abbandona: e questi medesimi effetti fanno ancora tutti gli aggregati di corpuscoli maggiori e maggiori, e di ogni figura, ancora che sferica, come veggiamo ne i monti di miglio, di grano, di migliarole di piombo e d'ogni altra materia. Ma se noi tenteremo di vedere tali accidenti nell'acqua, nissuno ve ne troveremo; ma, sollevata, immediatamente si spiana, se da vaso o altro esterno ritegno non sia sostenuta; incavata, subito scorre a riempire la cavità; ed agitata, per lunghissimo tempo va fluttuando, e per spazii grandissimi distendendo le sue onde. Da questo mi par di potere molto ragionevolmente arguire, i minimi dell'acqua, ne i quali ella pur sembra esser risoluta (poiché ha minor consistenza di qualsivoglia sottilissima polvere, anzi non ha consistenza nissuna), esser differentissimi da i minimi quanti e divisibili; né saprei ritrovarci altra differenza, che l'esser indivisibili. Parmi anco che la sua esquisitissima trasparenza ce ne porga assai ferma coniettura: perché se noi piglieremo del più trasparente cristallo che sia e lo cominceremo a rompere e pestare, ridotto in polvere perde la trasparenza, e sempre più quanto più sottilmente si trita; ma l'acqua, che pure è sommamente trita, è anco sommamente diafana. L'oro e l'argento, con acque forti polverizzati più sottilmente che con qualsivoglia lima, pur restano in polvere, ma non divengon fluidi, né prima si liquefanno che gl'indivisibili del fuoco o de i raggi del Sole gli dissolvano, credo ne i lor primi altissimi componenti, infiniti, indivisibili.

Sagr. Questo che V. S. ha toccato della luce, ho io più volte veduto con maraviglia; veduto, dico, con uno specchio concavo di tre palmi di diametro, liquefare il piombo in un instante: onde io son venuto in opinione, che quando lo specchio fusse grandissimo e ben terso e di figura parabolica, liquefarebbe non meno ogni altro metallo in brevissimo tempo, vedendo che quello, né molto grande né ben lustro e di cavità sferica, con tanta forza liquefaceva il piombo ed abbruciava ogni materia combustibile; effetti che mi rendon credibili le maraviglie de gli specchi d'Archimede.

Salv. Intorno a gli effetti de gli specchi d'Archimede mi rese credibile ogni miracolo, che si legge in più scrittori, la lettura de i libri dell'istesso Archimede, già da me con infinito stupore letti e studiati; e se nulla di dubbio mi fusse restato, quello che ultimamente ha dato in luce intorno allo Specchio Ustorio il P. Bonaventura Cavalieri, e che io con ammirazione ho letto, è bastato a cessarmi ogni difficoltà.

Sagr. Veddi ancor io cotesto trattato, e con gusto e maraviglia grande lo lessi; e perché per avanti avevo conoscenza della persona, mi andai confermando nel concetto che di esso avevo già preso, ch'ei fusse per riuscire uno de' principali matematici dell'età nostra. Ma tornando all'effetto maraviglioso de i raggi solari nel liquefare i metalli, doviamo noi credere che tale e sì veemente operazione sia senza moto, o pur che sia con moto, ma velocissimo?

Salv. Gli altri incendii e dissoluzioni veggiamo noi farsi con moto, e con moto velocissimo: veggansi le operazioni de i fulmini, della polvere nelle mine e ne i petardi, ed in somma quanto il velocitar co' i mantici la fiamma de i carboni, mista con vapori grossi e non puri, accresca di forza nel liquefare i metalli: onde io non saprei intendere che l'azzione della luce, benché purissima, potesse esser senza moto, ed anco velocissimo.

Sagr. Ma quale e quanta doviamo noi stimare che sia questa velocità del lume? forse instantanea, momentanea, o pur, come gli altri movimenti, temporanea? né potremo con esperienza assicurarci qual ella sia?

Simp. Mostra l'esperienza quotidiana, l'espansion del lume esser instantanea; mentre che vedendo in gran lontananza sparar un'artiglieria, lo splendor della fiamma senza interposizion di tempo si conduce a gli occhi nostri, ma non già il suono all'orecchie, se non dopo notabile intervallo di tempo.

Sagr. Eh, Sig. Simplicio, da cotesta notissima esperienza non si raccoglie altro se non che il suono si conduce al nostro udito in tempo men breve di quello che si conduca il lume; ma non mi assicura, se la venuta del lume sia per ciò istantanea, più che temporanea ma velocissima. Né simile osservazione conclude più che l'altra di chi dice: «Subito giunto il Sole all'orizonte, arriva il suo splendore a gli occhi nostri»; imperò che chi mi assicura che prima non giugnessero i suoi raggi al detto termine, che alla nostra vista?

Salv. La poca concludenza di queste e di altre simili osservazioni mi fece una volta pensare a qualche modo di poterci senza errore accertar, se l'illuminazione, cioè se l'espansion del lume, fusse veramente instantanea; poiché il moto assai veloce del suono ci assicura, quella della luce non poter esser se non velocissima: e l'esperienza che mi sovvenne, fu tale. Voglio che due piglino un lume per uno, il quale, tenendolo dentro lanterna o altro ricetto, possino andar coprendo e scoprendo, con l'interposizion della mano, alla vista del compagno, e che, ponendosi l'uno incontro all'altro in distanza di poche braccia, vadano addestrandosi nello scoprire ed occultare il lor lume alla vista del compagno, sì che quando l'uno vede il lume dell'altro, immediatamente scuopra il suo; la qual corrispondenza, dopo alcune risposte fattesi scambievolmente, verrà loro talmente aggiustata, che, senza sensibile svario, alla scoperta dell'uno risponderà immediatamente la scoperta dell'altro, sì che quando l'uno scuopre il suo lume, vedrà nell'istesso tempo comparire alla sua vista il lume dell'altro. Aggiustata cotal pratica in questa piccolissima distanza, pongansi i due medesimi compagni con due simili lumi in lontananza di due o tre miglia, e tornando di notte a far l'istessa esperienza, vadano osservando attentamente se le risposte delle loro scoperte ed occultazioni seguono secondo l'istesso tenore che facevano da vicino; che seguendo, si potrà assai sicuramente concludere, l'espansion del lume essere instantanea: ché quando ella ricercasse tempo, in una lontananza di tre miglia, che importano sei per l'andata d'un lume e venuta dell'altro, la dimora dovrebbe esser assai osservabile. E quando si volesse far tal osservazione in distanze maggiori, cioè di otto o dieci miglia, potremmo servirci del telescopio, aggiustandone un per uno gli osservatori al luogo dove la notte si hanno a mettere in pratica i lumi; li quali, ancor che non molto grandi, e per ciò invisibili in tanta lontananza all'occhio libero, ma ben facili a coprirsi e scoprirsi, con l'aiuto de i telescopii già aggiustati e fermati potranno esser commodamente veduti.

Sagr. L'esperienza mi pare d'invenzione non men sicura che ingegnosa. Ma diteci quello che nel praticarla avete concluso.

Salv. Veramente non l'ho sperimentata, salvo che in lontananza piccola, cioè manco d'un miglio, dal che non ho potuto assicurarmi se veramente la comparsa del lume opposto sia instantanea; ma ben, se non instantanea, velocissima, e direi momentanea, è ella, e per ora l'assimiglierei a quel moto che veggiamo farsi dallo splendore del baleno veduto tra le nugole lontane otto o dieci miglia; del qual lume distinguiamo il principio, e dirò il capo e fonte, in un luogo particolare tra esse nugole, ma bene immediatamente segue la sua espansione amplissima per le altre circostanti; che mi pare argomento, quella farsi con qualche poco di tempo; perché quando l'illuminazione fusse fatta tutta insieme, e non per parti, non par che si potesse distinguer la sua origine, e dirò il suo centro, dalle sue falde e dilatazioni estreme. Ma in quai pelaghi ci andiamo noi inavvertentemente pian piano ingolfando? tra i vacui, tra gl'infiniti, tra gli indivisibili, tra i movimenti instantanei, per non poter mai, dopo mille discorsi, giugnere a riva?

Sagr. Cose veramente molto sproporzionate al nostro intendimento. Ecco: l'infinito, cercato tra i numeri, par che vadia a terminar nell'unità; da gl'indivisibili nasce il sempre divisibile; il vacuo non par che risegga se non indivisibilmente mescolato tra 'l pieno: ed in somma in queste cose si muta talmente la natura delle comunemente intese da noi, che sin alla circonferenza d'un cerchio doventa una linea retta infinita; che, s'io ho ben tenuto a memoria, è quella proposizione che voi, Sig. Salviati, dovevi con geometrica dimostrazione far manifesta. Però, quando vi piaccia, sarà bene, senza più digredire, arrecarcela.

Salv. Eccomi a servirle, dimostrando per piena intelligenza il seguente problema:

Data una linea retta divisa secondo qualsivoglia proporzione in parti diseguali, descrivere un cerchio, alla cui circonferenza prodotte, a qualsivoglia punto di essa, due linee rette da i termini della data linea, ritenghino la proporzion medesima che hanno tra di loro le parti di essa linea data, sì che omologhe siano quelle che si partono da i medesimi termini.

Sia la data retta linea AB, divisa in qualsivoglia modo in parti diseguali nel punto C: bisogna descrivere il cerchio, a qualsivoglia punto della cui circonferenza concorrendo due rette prodotte da i termini A, B, abbiano tra di loro la proporzion medesima che hanno tra di loro le parti AC, BC, sì che omologhe sian quelle che si partono dall'istesso termine. Sopra 'l centro C, con l'intervallo della minor parte CB, intendasi descritto un cerchio, alla circonferenza del quale venga tangente dal punto A la retta AD, indeterminatamente prolungata verso E, e sia il contatto in D, e congiungasi la CD, che sarà perpendicolare alla AE; ed alla BA sia perpendicolare la BE, la quale prodotta concorrerà con la AE, essendo l'angolo A acuto; sia il concorso in E, di dove si ecciti la perpendicolare alla AE, che prodotta vadia a concorrere con la AB, infinitamente prolungata, in F: dico primieramente, le due rette FE, FC esser eguali. Imperò che, tirata la EC, aremo ne i due triangoli DEC, BEC li due lati dell'uno DE, EC eguali alli due dell'altro BE, EC, essendo le due DE, EB tangenti del cerchio DB, e le basi DC, CB parimente eguali; onde li due angoli DEC, BEC saranno eguali. E perché all'angolo BCE per esser retto manca quanto è l'angolo CEB, ed all'angolo CEF, pur per esser retto, manca quanto è l'angolo CED, essendo tali mancamenti eguali, gli angoli FCE, FEC saranno eguali, ed in consequenza i lati FE, FC; onde fatto centro il punto F, e con l'intervallo FE descrivendo un cerchio, passerà per il punto C. Descrivasi, e sia CEG: dico, questo esser il cerchio ricercato, a qualsivoglia punto della circonferenza del quale ogni coppia di linee che vi concorrano, partendosi da i termini A, B, aranno la medesima proporzione tra di loro che hanno le due parti AC, BC, le quali di già vi concorrono nel punto C. Questo, delle due che concorrono nel punto E, cioè delle AE, BE, è manifesto, essendo l'angolo E del triangolo AEB diviso in mezzo dalla CE; per lo che qual proporzione ha la AC alla CB, tale ha la AE alla BE. L'istesso proveremo delle due AG, BG, terminate nel punto G. Imperò che, essendo (per la similitudine de' triangoli AFE, EFB) come AF ad FE così EF ad FB, cioè come AF ad FC così CF ad FB, sarà, dividendo, come AC a CF (cioè ad FG) così CB a FB, e tutta AB a tutta BG come una CB ad una BF, e, componendo, come AG a GB così CF ad FB, cioè FE ad FB, cioè AE ad EB, ed AC a CB: il che bisognava provare. Prendasi ora qualsivoglia altro punto nella circonferenza, e sia H, al quale concorrano le due AH, BH: dico parimente, come AC a CB, così essere AH ad HB. Prolunghisi HB sino alla circonferenza in I, e congiungasi IF: e perché già si è visto, come AB a BG, così essere CB a BF, sarà il rettangolo ABF eguale al rettangolo CBG, cioè IBH, e però come AB a BH, così IB a BF; e sono gli angoli al B eguali; adunque AH ad HB sta come IF, cioè EF, ad FB, ed AE ad EB.

Dico, oltre a ciò, che è impossibile che le linee che abbiano tal proporzione, partendosi da i termini A, B, concorrano a verun punto o dentro o fuori del cerchio CEG. Imperò che, se è possibile, concorrano due tali linee al punto L, posto fuori, e siano le AL, BL, e prolunghisi la LB sino alla circonferenza in M, e congiungasi MF. Se dunque la AL alla BL è come la AC alla BC, cioè come la MF alla FB, aremo due triangoli ALB, MFB, li quali intorno alli due angoli ALB, MFB hanno i lati proporzionali, gli angoli alla cima nel punto B eguali, e li due rimanenti FMB, LAB minori che retti (imperò che l'angolo retto al punto M ha per base tutto il diametro CG, e non la sola parte BF; e l'altro al punto A è acuto, perché la linea AL, omologa della AC, è maggiore della BL, omologa della BC); adunque i triangoli ABL, MBF son simili, e però come AB a BL così MB a BF, onde il rettangolo ABF sarà eguale al rettangolo MBL: ma il rettangolo ABF s'è dimostrato eguale al CBG: adunque il rettangolo MBL è eguale al rettangolo CBG, il che è impossibile: adunque il concorso non può cader fuor del cerchio. E nel medesimo modo si dimostrerà, non poter cader dentro: adunque tutti i concorsi cascano nella circonferenza stessa.

Ma è tempo che torniamo a dar sodisfazione al desiderio del Sig. Simplicio, mostrandogli come il risolver la linea ne' suoi infiniti punti non è non solamente impossibile, ma né meno ha in sé maggior difficoltà che 'l distinguere le sue parti quante, fatto però un supposto, il quale penso, Sig. Simplicio, che non siate per negarmi: e questo è, che non mi ricercherete che io vi separi i punti l'uno dall'altro e ve li faccia veder a uno a uno distinti sopra questa carta, perché io ancora mi contenterei che, senza staccar l'una dall'altra le quattro o le sei parti d'una linea, mi mostraste le sue divisioni segnate, o al più piegate ad angoli, formandone un quadrato o un essagono; perché mi persuado pure che allora le chiamereste a bastanza distinte ed attuate.

Simp. Veramente sì.

Salv. Ora, se l'inflettere una linea ad angoli, formandone ora un quadrato, ora un ottangolo, ora un poligono di quaranta, di cento o mille angoli, è mutazione bastante a ridurre all'atto quelle quattro, otto, quaranta, cento e mille parti che prima nella linea diritta erano, per vostro detto, in potenza, quando io formi di lei un poligono di lati infiniti, cioè quando io la infletta nella circonferenza d'un cerchio, non potrò io con pari licenza dire d'aver ridotto all'atto quelle parti infinite, che voi prima, mentre era retta, dicevi esser in lei contenute in potenza? Né si può negare, tal risoluzione esser fatta ne' suoi infiniti punti non meno che quella delle sue quattro parti nel formarne un quadrato, o nelle sue mille nel formarne un millagono; imperò che in lei non manca veruna delle condizioni che si trovano nel poligono di mille e di cento mila lati. Questo, applicato a una linea retta, se gli posa sopra toccandola con uno de' suoi lati, cioè con una sua centomillesima parte; il cerchio, che è un poligono di lati infiniti, tocca la medesima retta con uno de' suoi lati, che è un sol punto, diverso da tutti i suoi collaterali, e perciò da quelli diviso e distinto non meno che un lato del poligono da i suoi conterminali: e come il poligono rivoltato sopra un piano stampa con i toccamenti conseguenti de' suoi lati una linea retta eguale al suo perimetro, così il cerchio girato sopra un tal piano descrive con gl'infiniti suoi successivi contatti una linea retta egual alla propria circonferenza. Non so adesso, Sig. Simplicio, se i Signori Peripatetici, a i quali io ammetto, come verissimo concetto, il continuo esser divisibile in sempre divisibili, sì che continuando una tal divisione e suddivisione mai non si perverrebbe alla fine, si contenteranno di concedere a me, niuna delle tali loro divisioni esser l'ultima, come veramente non è, poiché sempre ve ne resta un'altra, ma bene l'ultima ed altissima esser quella che lo risolve in infiniti indivisibili, alla quale concedo che non si perverrebbe mai dividendo successivamente in maggiore e maggior moltitudine di parti; ma servendosi della maniera che propongo io, di distinguere e risolvere tutta la infinità in un tratto solo (artifizio che non mi dovrebbe esser negato), crederei che dovessero quietarsi, ed ammetter questa composizione del continuo di atomi assolutamente indivisibili, e massime essendo questa una strada forse più d'ogni altra corrente per trarci fuori di molto intrigati laberinti, quali sono, oltre a quello già toccato dalla coerenza delle parti de i solidi, il comprender come stia il negozio della rarefazzione e della condensazione, senza incorrer per causa di quella nell'inconveniente di dovere ammettere spazii vacui, e per questa la penetrazione de i corpi: inconvenienti, che amendue mi pare ch'assai destramente vengano schivati con l'ammetter detta composizione d'indivisibili.

Simp. Io non so quello che i Peripatetici fusser per dire, atteso che le considerazioni fatte da voi credo che gli giugnerebbero per la maggior parte nuove, e come tali converrebbe esaminarle; e potrebbe accadere che quelli vi ritrovassero risposte e soluzioni potenti a sciorre quei nodi, che io, per la brevità del tempo e per la debolezza del mio ingegno, non saprei di presente risolvere. Però sospendendo per ora questa parte, sentirei ben volentieri come l'introduzzione di questi indivisibili faciliti l'intelligenza della condensazione e della rarefazzione, schivando nell'istesso tempo il vacuo e la penetrazion de i corpi.

Sagr. Sentirò io ancora con gran brama la medesima cosa, all'intelletto mio tanto oscura; con questo però, che io non rimanga defraudato di sentire, conforme a quello che poco fa disse il Sig. Simplicio, le ragioni d'Aristotele in confutazion del vacuo, ed in consequenza le soluzioni che voi gli arrecate, come convien fare mentre voi ammettete quello che esso nega.

Salv. Faremo l'uno e l'altro. E quanto al primo, è necessario che, sì come in grazia della rarefazzione ci serviamo della linea descritta dal minor cerchio, maggiore della propria circonferenza, mentre vien mosso alla revoluzione del maggiore, così per intelligenza della condensazione mostriamo come alla conversione fatta dal minor cerchio il maggiore descriva una linea retta minore della sua circonferenza; per la cui più chiara esplicazione, porremo innanzi la considerazione di quello che accade ne i poligoni.

In una descrizzione simile a quell'altra, siano due essagoni circa il comune centro L, che siano questi ABC, HIK, con le linee parallele HOM, ABc, sopra le quali si abbiano a far le revoluzioni; e fermato l'angolo I del poligono minore, volgasi esso poligono sin che il lato IK caschi sopra la parallela, nel qual moto il punto K descriverà l'arco KM, e 'l lato KI si unirà con la parte IM: tra tanto bisogna vedere quel che farà il lato CB del poligono maggiore. E perché il rivolgimento si fa sopra il punto I, la linea IB col termine suo B descriverà, tornando indietro, l'arco Bb sotto alla parallela cA, tal che quando il lato KI si congiugnerà con la linea MI, il lato BC si unirà con la linea bc, con l'avanzarsi per l'innanzi solamente quanto è la parte Bc e ritirando in dietro la parte suttesa all'arco Bb, la quale vien sopraposta alla linea BA. Ed intendendo continuarsi nell'istesso modo la conversione fatta dal minor poligono, questo descriverà bene e passerà sopra la sua parallela una linea eguale al suo perimetro; ma il maggiore passerà una linea minore del suo perimetro la quantità di tante linee bB quanti sono uno manco de' suoi lati; e sarà tal linea prossimamente eguale alla descritta dal poligono minore, eccedendola solamente di quanto è la bB. Qui dunque senza veruna repugnanza si scorge la cagione per la quale il maggior poligono non trapassi (portato dal minore) con i suoi lati linea maggiore della passata dal minore; che è perché una parte di ciascheduno de' lati si soprappone al suo precedente conterminale.

Ma se considereremo i due cerchi intorno al centro A, li quali sopra le lor parallele posino, toccando il minore la sua nel punto B, ed il maggiore la sua nel punto C, qui nel cominciar a far la revoluzione del minore non avverrà che il punto B resti per qualche tempo immobile, sì che la linea BC dando in dietro trasporti il punto C, come accadeva ne i poligoni, che restando fisso il punto I sin che il lato KI cadesse sopra la linea IM, la linea IB riportava in dietro il B, termine del lato CB, sino in b, onde il lato BC cadeva in bc, soprapponendo alla linea BA la parte Bb e solo avanzandosi per l'innanzi la parte Bc, eguale alla IM, cioè a un lato del poligono minore; per le quali soprapposizioni, che sono gli eccessi de i lati maggiori sopra i minori, gli avanzi che restano, eguali a i lati del minor poligono, vengono a comporre nell'intera revoluzione la linea retta eguale alla segnata e misurata dal poligono minore. Ma qui dico, che se noi vorremo applicare un simil discorso all'effetto de i cerchi, converrà dire, che dove i lati di qualsivoglia poligono son compresi da qualche numero, i lati del cerchio sono infiniti: quelli son quanti e divisibili; questi, non quanti e indivisibili: i termini de i lati del poligono nella revoluzione stanno per qualche tempo fermi, cioè ciascheduno tal parte del tempo di una intera conversione, qual parte esso è di tutto il perimetro; ne i cerchi similmente le dimore de' termini de' suoi infiniti lati son momentanee, perché tal parte è un instante d'un tempo quanto, qual è un punto d'una linea, che ne contiene infiniti: i regressi in dietro fatti da i lati del maggior poligono sono non di tutto 'l lato, ma solamente dell'eccesso suo sopra 'l lato del minore, acquistando per l'innanzi tanto di spazio quanto è il detto minor lato; ne i cerchi il punto o lato C, nella quiete instantanea del termine B, si ritira in dietro quanto è il suo eccesso sopra 'l lato B, acquistando per l'innanzi quanto è il medesimo B: ed in somma gl'infiniti lati indivisibili del maggior cerchio con gl'infiniti indivisibili ritiramenti loro, fatti nell'infinite instantanee dimore de gl'infiniti termini de gl'infiniti lati del minor cerchio, e con i loro infiniti progressi, eguali a gl'infiniti lati di esso minor cerchio, compongono e disegnano una linea eguale alla descritta dal minor cerchio, contenente in sé infinite soprapposizioni non quante, che fanno una costipazione e condensazione senza veruna penetrazione di parti quante, quale non si può intendere farsi nella linea divisa in parti quante, quale è il perimetro di qualsivoglia poligono, il quale, disteso in linea retta, non si può ridurre in minor lunghezza se non col far che i lati si soprapponghino e penetrino l'un l'altro. Questa costipazione di parti non quante ma infinite, senza penetrazione di parti quante, e la prima distrazzione di sopra dichiarata de gl'infiniti indivisibili con l'interposizione di vacui indivisibili, credo che sia il più che dir si possa per la condensazione e rarefazzione de i corpi, senza necessità d'introdurre la penetrazione de i corpi e gli spazii quanti vacui. Se ci è cosa che vi gusti, fatene capitale; se no, reputatela vana, e 'l mio discorso ancora, e ricercate da qualche altro esplicazione di maggior quiete per l'intelletto. Solo queste due parole vi replico, che noi siamo tra gl'infiniti e gl'indivisibili.

Sagr. Che il pensiero sia sottile, ed a' miei orecchi nuovo e peregrino, lo confesso liberamente; se poi nel fatto stesso la natura proceda con tal ordine, non saprei che risolvermi: vero è che sin ch'io non sentissi cosa che maggiormente mi quietassi, per non rimaner muto affatto, m'atterrei a questa. Ma forse il Sig. Simplicio avrà (quello che sin qui non ho incontrato) modo di esplicare l'esplicazione che in materia così astrusa da i filosofi si arreca; ché in vero quel che sin qui ho letto circa la condensazione è per me così denso, e quel della rarefazzione così sottile, che la mia debol vista questo non comprende e quello non penetra.

Simp. Io son pieno di confusione, e trovo duri intoppi nell'un sentiero e nell'altro, ed in particolare in questo nuovo: perché, secondo questa regola, un'oncia d'oro si potrebbe rarefare e distrarre in una mole maggiore di tutta la Terra, e tutta la Terra condensare e ridurre in minor mole di una noce, cose che io non credo, né credo che voi medesimo crediate; e le considerazioni e dimostrazioni sin qui fatte da voi, come che son cose matematiche, astratte e separate dalla materia sensibile, credo che applicate alle materie fisiche e naturali non camminerebbero secondo coteste regole.

Salv. Che io vi sia per far vedere l'invisibile, né io lo saprei fare, né credo voi lo ricerchiate; ma per quanto da i nostri sensi può esser compreso, già che voi avete nominato l'oro, non veggiam noi farsi immensa distrazzione delle sue parti? Non so se vi sia occorso di veder le maniere che tengono gli artefici in condur l'oro tirato, il quale non è veramente oro se non in superficie, ma la materia interna è argento: ed il modo del condurlo è tale. Pigliano un cilindro, o volete dire una verga, d'argento, lunga circa mezzo braccio e grossa per tre o quattro volte il dito pollice, e questa indorano con foglie d'oro battuto, che sapete esser così sottile che quasi va vagando per l'aria, e di tali foglie ne soprappongono otto o dieci, e non più. Dorato che è, cominciano a tirarlo con forza immensa, facendolo passare per fori della filiera; e tornando a farlo ripassare molte e molte volte successivamente per fori più angusti, dopo molte e molte ripassate lo riducono alla sottigliezza d'un capello di donna, se non maggiore: e tuttavia resta dorato in superficie. Lascio ora considerare a voi quale sia la sottigliezza e distrazzione alla quale si è ridotta la sustanza dell'oro.

Simp. Io non veggo che da questa operazione venga in consequenza un assottigliamento della materia dell'oro da farne quelle maraviglie che voi vorreste: prima, perché già la prima doratura fu di dieci foglie d'oro, che vengono a far notabile grossezza; secondariamente, se ben, nel tirare e assottigliar quell'argento, cresce in lunghezza, scema però anco tanto in grossezza, che, compensando l'una dimensione con l'altra, la superficie non si agumenta tanto, che per vestir l'argento di oro, bisogni ridurlo a sottigliezza maggiore di quella delle prime foglie.

Salv. V'ingannate d'assai, Sig. Simplicio, perché l'accrescimento della superficie è sudduplo dell'allungamento, come io potrei geometricamente dimostrarvi.

Sagr. Io, e per me e per il Sig. Simplicio, vi pregherei a recarci tal dimostrazione, se però credete che da noi possa esser capita.

Salv. Vedrò se così improvisamente mi torna a memona. Già è manifesto, che quel primo grosso cilindro d'argento ed il filo lunghissimo tirato sono due cilindri eguali, essendo l'istesso argento; tal che s'io mostrerò qual proporzione abbiano tra di loro le superficie de i cilindri eguali, averemo l'intento. Dico per tanto che:

Le superficie de i cilindri eguali, trattone le basi, son tra di loro in sudduplicata proporzione delle loro lunghezze.

Siano due cilindri eguali, l'altezze de i quali AB, CD, e sia la linea E media proporzionale tra esse: dico, la superficie del cilindro AB, trattone le basi, alla superficie del cilindro CD, trattone parimente le basi, aver la medesima proporzione che la linea AB alla linea E, che è suddupla dalla proporzione di AB a CD. Taglisi la parte del cilindro AB in F, e sia l'altezza AF eguale alla CD: e perché le basi de' cilindri eguali rispondon contrariamente alle loro altezze, il cerchio base del cilindro CD al cerchio base del cilindro AB sarà come l'altezza BA alla DC; e perché i cerchi son tra loro come i quadrati de i diametri, aranno detti quadrati la medesima proporzione che la BA alla CD; ma come BA a CD, così il quadrato BA al quadrato della E: son dunque tali quattro quadrati proporzionali; e però i lor lati ancora saranno proporzionali, e come la linea AB alla E, così il diametro del cerchio C al diametro del cerchio A. Ma come i diametri, così sono le circonferenze, e come le circonferenze così sono ancora le superficie de' cilindri egualmente alti: adunque come la linea AB alla E, così la superficie del cilindro CD alla superficie del cilindro AF. Perché dunque l'altezza AF alla AB sta come la superficie AF alla superficie AB; e come l'altezza AB alla linea E, così la superficie CD alla AF: sarà, per la perturbata, come l'altezza AF alla E, così la superficie CD alla superficie AB: e convertendo, come la superficie del cilindro AB alla superficie del cilindro CD, così la linea E alla AF, cioè alla CD, o vero la AB alla E, che è proporzione suddupla della AB alla CD: che è quello che bisognava provare.

Ora, se noi applicheremo questo, che si è dimostrato, al nostro proposito, presupposto che quel cilindro d'argento, che fu dorato mentre non era più lungo di mezzo braccio e grosso tre o quattro volte più del dito pollice, assottigliato alla finezza d'un capello si sia allungato sino in venti mila braccia (che sarebbe anche più assai), troveremo, la sua superficie esser cresciuta dugento volte più di quello che era; ed in consequenza quelle foglie d'oro, che furon soprapposte dieci in numero, distese in superficie dugento volte maggiore, ci assicurano, l'oro, che cuopre la superficie delle tante braccia di filo, restar non più grosso che la ventesima parte d'una foglia dell'ordinario oro battuto. Considerate ora voi qual sia la sua sottigliezza, e se è possibile concepirla fatta senza una immensa distrazzione di parti, e se questa vi pare una esperienza che tenda anche ad una composizione d'infiniti indivisibili nelle materie fisiche: se ben di ciò non mancano altri più gagliardi e concludenti rincontri.

Sagr. La dimostrazione mi par tanto bella, che quando non avesse forza di persuader quel primo intento per il quale è stata prodotta (che pur mi par che ve l'abbia grande), ad ogni modo benissimo si è impiegato questo breve tempo che per sentirla si è speso.

Salv. Già che veggo che gustate tanto di queste geometriche dimostrazioni, apportatrici di guadagni sicuri, vi dirò la compagna di questa, che sodisfà ad un quesito curioso assai. Nella passata aviamo quello che accaggia de i cilindri eguali, ma diversi di altezze o vero lunghezze: è ben sentire quello che avvenga a i cilindri eguali di superficie, ma diseguali d'altezze; intendendo sempre delle superficie sole che gli circondano intorno, cioè non comprendendo le due basi, superiore e inferiore. Dico dunque che:

I cilindri retti, le superfici de i quali, trattone le basi, siano eguali, hanno fra di loro la medesima proporzione che le loro altezze contrariamente prese.

Siano eguali le superficie de i due cilindri AE, CF, ma l'altezza di questo CD maggiore dell'altezza dell'altro AB: dico, il cilindro AE al cilindro CF aver la medesima proporzione che l'altezza CD alla AB. Perché dunque la superficie CF è uguale alla superficie AE, sarà il cilindro CF minore dell'AE, perché se li fusse eguale, la sua superficie, per la passata proposizione, sarebbe maggiore della superficie AE, e molto più se il medesimo cilindro CF fusse maggiore dell'AE. Intendasi il cilindro ID eguale all'AE; adunque, per la precedente, la superficie del cilindro ID alla superficie dell'AE starà come l'altezza IF alla media tra IF, AB. Ma essendo, per il dato, la superficie AE eguale alla CF, ed avendo la superficie ID alla CF la medesima proporzione che l'altezza IF alla CD, adunque la CD è media tra le IF, AB; in oltre, essendo il cilindro ID eguale al cilindro AE, aranno amendue la medesima proporzione al cilindro CF: ma l'ID al CF sta come l'altezza IF alla CD: adunque il cilindro AE al cilindro CF arà la medesima proporzione che la linea IF alla CD, cioè che la CD alla AB, che è l'intento.

Di qui s'intende la ragione d'un accidente che non senza maraviglia vien sentito dal popolo; ed è, come possa essere che il medesimo pezzo di tela più lungo per un verso che per l'altro, se se ne facesse un sacco da tenervi dentro del grano, come si costuma fare con un fondo di tavola, terrà più servendoci per l'altezza del sacco della minor misura della tela e con l'altra circondando la tavola del fondo, che facendo per l'opposito: come se, v. g., la tela per un verso fusse sei braccia e per l'altro dodici, più terrà quando con la lunghezza di dodici si circondi la tavola del fondo, restando il sacco alto braccia sei, che se si circondasse un fondo di sei braccia, avendone dodici per altezza. Ora, da quello che si è dimostrato, alla generica notizia del capir più per quel verso che per questo, si aggiugne la specifica e particolare scienza del quanto ei contenga più; che è, che tanto più terrà quanto sarà più basso, e tanto meno quanto più alto: e così, nelle misure assegnate essendo la tela il doppio più lunga che larga, cucita per la lunghezza terrà la metà manco che per l'altro verso; e parimente avendo una stuoia, per fare una bugnola, lunga venticinque braccia e larga, v. g., sette, piegata per lo lungo terrà solamente sette misure di quelle che per l'altro verso ne terrebbe venticinque.

Sagr. E così con nostro gusto particolare andiamo continuamente acquistando nuove cognizioni curiose e non ignude di utilità. Ma nel proposito toccato adesso, veramente non credo che tra quelli che mancano di qualche cognizione di geometria se ne trovassero quattro per cento che non restassero a prima giunta ingannati, che quei corpi che da superficie eguali son contenuti, non fussero ancora in tutto eguali; sì come nell'istesso errore incorrono parlando delle superficie, che per determinar, come spesse volte accade, delle grandezze di diverse città, intera cognizione gli par d'averne qualunque volta sanno la quantità de i recinti di quelle, ignorando che può essere un recinto eguale a un altro, e la piazza contenuta da questo assai maggiore della piazza di quello: il che accade non solamente tra le superficie irregolari, ma tra le regolari, delle quali quelle di più lati son sempre più capaci di quelle di manco lati, sì che in ultimo il cerchio, come poligono di lati infiniti, è capacissimo sopra tutti gli altri poligoni di egual circuito; di che mi ricordo averne con gusto particolare veduta la dimostrazione studiando la Sfera del Sacrobosco con un dottissimo commentario sopra.

Salv. È verissimo: ed avendo io ancora incontrato cotesto luogo, mi dette occasione di ritrovare, come con una sola e breve dimostrazione si concluda, il cerchio esser maggiore di tutte le figure regolari isoperimetre; e, dell'altre, quelle di più lati, maggiori di quelle di manco.

Sagr. Ed io, che sento tanto diletto in certe proposizioni e dimostrazioni scelte e non triviali, importunandovi vi prego che me ne facciate partecipe.

Salv. In brevi parole vi spedisco, dimostrando il seguente teorema, cioè:

Il cerchio è medio proporzionale tra qualsivoglino due poligoni regolari tra di loro simili, de i quali uno gli sia circoscritto e l'altro gli sia isoperimetra. In oltre, essendo egli minore di tutti i circoscritti, all'incontro massimo di tutti gl'isoperimetri. De i medesimi poi circoscritti, quelli che hanno più angoli son minori di quelli che ne hanno manco; ma all'incontro, de gl'isoperimetri quelli di più angoli son maggiori.

Delli due poligoni simili A, B sia l'A circoscritto al cerchio A, e l'altro B ad esso cerchio sia isoperimetro: dico, il cerchio esser medio proporzionale tra essi. Imperò che (tirato il semidiametro AC), essendo il cerchio eguale a quel triangolo rettangolo, de i lati del quale che sono intorno all'angolo retto, uno sia eguale al semidiametro AC e l'altro alla circonferenza; e similmente essendo il poligono A eguale al triangolo rettangolo, che intorno all'angolo retto ha uno de i lati eguali alla medesima retta AC, e l'altro al perimetro del medesimo poligono; è manifesto, il circoscritto poligono aver al cerchio la medesima proporzione che ha il suo perimetro alla circonferenza di esso cerchio, cioè al perimetro del poligono B, che alla circonferenza detta si pone eguale: ma il poligono A al B ha doppia proporzione che 'l suo perimetro al perimetro di B (essendo figure simili): adunque il cerchio A è medio proporzionale tra i due poligoni A, B. Ed essendo il poligono A maggior del cerchio A, è manifesto, esso cerchio A esser maggiore del poligono B suo isoperimetro, ed in consequenza massimo di tutti i poligoni regolari suoi isoperimetri.

Quanto all'altra parte, cioè di provare che de i poligoni circoscritti al medesimo cerchio, quello di manco lati sia maggior di quello di più lati; ma che all'incontro, de i poligoni isoperimetri quello di più lati sia maggiore di quello di manco lati; dimostreremo così. Nel cerchio, il cui centro O, semidiametro OA, sia la tangente AD, ed in essa pongasi, per esempio, AD esser la metà del lato del pentagono circoscritto, ed AC metà del lato dell'ettagono, e tirinsi le rette OGC, OFD, e, centro O, intervallo OC, descrivasi l'arco ECI. E perché il triangolo DOC è maggiore del settore EOC, e 'l settore COI maggiore del triangolo COA, maggior proporzione arà il triangolo DOC al triangolo COA, che 'l settore EOC al settore COI, cioè che 'l settore FOG al settore GOA; e componendo e permutando, il triangolo DOA al settore FOA arà maggior proporzione che il triangolo COA al settore GOA, e dieci triangoli DOA a dieci settori FOA aranno maggior proporzione che quattordici triangoli COA a quattordici settori GOA, cioè il pentagono circoscritto arà maggior proporzione al cerchio che non gli ha l'ettagono; e però il pentagono sarà maggior dall'ottagono. Intendansi ora un ettagono ed un pentagono isoperimetri al medesimo cerchio: dico, l'ettagono esser maggior del pentagono. Imperò che, essendo l'istesso cerchio medio proporzionale tra 'l pentagono circoscritto e 'l pentagono suo isoperimetro, e parimente medio tra 'l circoscritto e l'isoperimetro ettagono; essendosi provato, il circoscritto pentagono esser maggiore del circoscritto ettagono; avrà esso pentagono maggior proporzione al cerchio che l'ettagono, cioè il cerchio arà maggior proporzione al suo isoperimetro pentagono che all'isoperimetro ettagono: adunque il pentagono è minore dell'isoperimetro ettagono: che si doveva dimostrare.

Sagr. Gentilissima dimostrazione e molto acuta. Ma dove siamo trascorsi a ingolfarci nella geometria? mentre eramo su 'l considerare le difficoltà promosse dal Sig. Simplicio, che veramente son di gran considerazione; ed in particolare quella della condensazione mi par durissima.

Salv. Se la condensazione e la rarefazzione son moti opposti, dove si vegga una immensa rarefazzione, non si potrà negare una non men grandissima condensazione; ma rarefazzioni immense, e, quel che accresce la maraviglia, quasi che momentanee, le veggiamo noi tutto 'l giorno. E quale sterminata rarefazzione è quella di una poca quantità di polvere d'artiglieria, risoluta in una mole vastissima di fuoco? e quale, oltre a questa, l'espansione, direi quasi senza termine, della sua luce? E se quel fuoco e questo lume si riunissero insieme, che pur non è impossibile, poiché dianzi stettero dentro quel piccolo spazio, qual condensamento sarebbe questo? Voi, discorrendo, troverete mille di tali rarefazzioni, che sono molto più in pronto ad esser osservate che le condensazioni, perché le materie dense son più trattabili e sottoposte a i nostri sensi, che ben maneggiamo le legne e le vediamo risolvere in fuoco e in luce, ma non così veggiamo il fuoco e 'l lume condensarsi a costituire il legno; veggiamo i frutti, i fiori e mille altre solide materie risolversi in gran parte in odori, ma non così osserviamo gli atomi odorosi concorrere alla costituzione de i solidi odorati. Ma dove manca la sensata osservazione, si deve supplir col discorso, che basterà per farci capaci non men del moto alla rarefazzione e resoluzione de i solidi, che alla condensazione delle sustanze tenui e rarissime. In oltre, noi trattiamo come si possa far la condensazione e rarefazzione de i corpi che si possono rarefare e condensare, specolando in qual maniera ciò possa esser fatto senza l'introduzzion del vacuo e della penetrazione de i corpi; il che non esclude che in natura possano esser materie che non ammettono tali accidenti, ed in consequenza non danno luogo a quelli che voi chiamate inconvenienti e impossibili. E finalmente. Sig. Simplicio, io, in grazia di voi altri, Signori filosofi, mi sono affaticato in specolare come si possa intendere, farsi la condensazione e la rarefazzione senza ammetter la penetrazione de i corpi e l'introduzzione de gli spazii vacui, effetti da voi negati ed aborriti; che quando voi gli voleste concedere, io non vi sarei così duro contradittore. Però, o ammettete questi inconvenienti, o gradite le mie specolazioni, o trovatene di più aggiustate.

Sagr. Alla negativa della penetrazione son io del tutto con i filosofi peripatetici. A quella del vacuo vorrei sentir ben ponderare la dimostrazione d'Aristotele, con la quale ei l'impugna, e quello che voi, Sig. Salviati, gli opponete. Il Sig. Simplicio mi farà grazia di arrecar puntualmente la prova del Filosofo, e voi Sig. Salviati, la risposta.

Simp. Aristotele, per quanto mi sovviene, insurge contro alcuni antichi, i quali introducevano il vacuo come necessario per il moto, dicendo che questo senza quello non si potrebbe fare. A questo contrapponendosi Aristotele, dimostra che, all'opposito, il farsi (come veggiamo) il moto distrugge la posizione del vacuo; e 'l suo progresso è tale. Fa due supposizioni: l'una è di mobili diversi in gravità, mossi nel medesimo mezzo; l'altra è dell'istesso mobile mosso in diversi mezzi. Quanto al primo, suppone che mobili diversi in gravità si muovano nell'istesso mezzo con diseguali velocità, le quali mantengano tra di loro la medesima proporzione che le gravità; sì che, per esempio, un mobile dieci volte più grave di un altro si muova dieci volte più velocemente. Nell'altra posizione piglia che le velocità del medesimo mobile in diversi mezzi ritengano tra di loro la proporzione contraria di quella che hanno le grossezze o densità di essi mezzi; talmente che, posto, v. g., che la crassizie dell'acqua fusse dieci volte maggiore di quella dell'aria, vuole che la velocità nell'aria sia dieci volte più che la velocità nell'acqua. E da questo secondo supposto trae la dimostrazione in cotal forma; Perché la tenuità del vacuo supera d'infinito intervallo la corpulenza, ben che sottilissima, di qualsivoglia mezzo pieno, ogni mobile che nel mezzo pieno si movesse per qualche spazio in qualche tempo, nel vacuo dovrebbe muoversi in uno istante; ma farsi moto in uno instante è impossibile; adunque darsi il vacuo in grazia del moto è impossibile.

Salv. L'argomento si vede che è ad hominem, cioè contro a quelli che volevano il vacuo come necessario per il moto: che se io concederò l'argomento come concludente, concedendo insieme che nel vacuo non si farebbe il moto, la posizion del vacuo, assolutamente presa e non in relazione al moto, non vien destrutta. Ma per dire quel che per avventura potrebber rispondere quegli antichi, acciò meglio si scorga quanto concluda la dimostrazione d'Aristotele, mi par che si potrebbe andar contro a gli assunti di quello, negandogli amendue. E quanto al primo, io grandemente dubito che Aristotele non sperimentasse mai quanto sia vero che due pietre, una più grave dell'altra dieci volte, lasciate nel medesimo instante cader da un'altezza, v. g., di cento braccia, fusser talmente differenti nelle lor velocità, che all'arrivo della maggior in terra, l'altra si trovasse non avere né anco sceso dieci braccia.

Simp. Si vede pure dalle sue parole ch'ei mostra d'averlo sperimentato, perché ei dice: Veggiamo il più grave; or quel vedersi accenna l'averne fatta l'esperienza.

Sagr. Ma io, Sig. Simplicio, che n'ho fatto la prova, vi assicuro che una palla d'artiglieria, che pesi cento, dugento e anco più libbre, non anticiperà di un palmo solamente l'arrivo in terra della palla d'un moschetto, che ne pesi una mezza, venendo anco dall'altezza di dugento braccia.

Salv. Ma, senz'altre esperienze, con breve e concludente dimostrazione possiamo chiaramente provare, non esser vero che un mobile più grave si muova più velocemente d'un altro men grave, intendendo di mobili dell'istessa materia, ed in somma di quelli de i quali parla Aristotele. Però ditemi, Sig. Simplicio, se voi ammettete che di ciascheduno corpo grave cadente sia una da natura determinata velocità, sì che accrescergliela o diminuirgliela non si possa se non con usargli violenza o opporgli qualche impedimento.

Simp. Non si può dubitare che l'istesso mobile nell'istesso mezzo abbia una statuita e da natura determinata velocità, la quale non se gli possa accrescere se non con nuovo impeto conferitogli, o diminuirgliela salvo che con qualche impedimento che lo ritardi.

Salv. Quando dunque noi avessimo due mobili, le naturali velocità de i quali fussero ineguali, è manifesto che se noi congiugnessimo il più tardo col più veloce, questo dal più tardo sarebbe in parte ritardato, ed il tardo in parte velocitato dall'altro più veloce. Non concorrete voi meco in quest'opinione?

Simp. Parmi che così debba indubitabilmente seguire.

Salv. Ma se questo è, ed è insieme vero che una pietra grande si muova, per esempio, con otto gradi di velocità, ed una minore con quattro, adunque, congiugnendole amendue insieme, il composto di loro si moverà con velocità minore di otto gradi: ma le due pietre, congiunte insieme, fanno una pietra maggiore che quella prima, che si moveva con otto gradi di velocità: adunque questa maggiore si muove men velocemente che la minore; che è contro alla vostra supposizione. Vedete dunque come dal suppor che 'l mobile più grave si muova più velocemente del men grave, io vi concludo, il più grave muoversi men velocemente.

Simp. Io mi trovo avviluppato, perché mi par pure che la pietra minore aggiunta alla maggiore le aggiunga peso, e aggiugnendole peso, non so come non debba aggiugnerle velocità, o almeno non diminuirgliela.

Salv. Qui commettete un altro errore, Sig. Simplicio, perché non è vero che quella minor pietra accresca peso alla maggiore.

Simp. Oh, questo passa bene ogni mio concetto.

Salv. Non lo passerà altrimente, fatto ch'io v'abbia accorto dell'equivoco nel quale voi andate fluttuando: però avvertite che bisogna distinguere i gravi posti in moto da i medesimi costituiti in quiete. Una gran pietra messa nella bilancia non solamente acquista peso maggiore col soprapporgli un'altra pietra, ma anco la giunta di un pennecchio di stoppa la farà pesar più quelle sei o dieci once che peserà la stoppa; ma se voi lascerete liberamente cader da un'altezza la pietra legata con la stoppa, credete voi che nel moto la stoppa graviti sopra la pietra, onde gli debba accelerar il suo moto, o pur credete che ella la ritarderà, sostenendola in parte? Sentiamo gravitarci su le spalle mentre vogliamo opporci al moto che farebbe quel peso che ci sta addosso; ma se noi scendessimo con quella velocità che quel tal grave naturalmente scenderebbe, in che modo volete che ci prema e graviti sopra? Non vedete che questo sarebbe un voler ferir con la lancia colui che vi corre innanzi con tanta velocità, con quanta o con maggiore di quella con la quale voi lo seguite? Concludete pertanto che nella libera e naturale caduta la minor pietra non gravita sopra la maggiore, ed in consequenza non le accresce peso, come fa nella quiete.

Simp. Ma chi posasse la maggior sopra la minore?

Salv. Le accrescerebbe peso, quando il suo moto fusse più veloce: ma già si è concluso che quando la minore fusse più tarda, ritarderebbe in parte la velocità della maggiore, tal che il loro composto si moverebbe men veloce, essendo maggiore dell'altra; che è contro al vostro assunto. Concludiamo per ciò, che i mobili grandi e i piccoli ancora, essendo della medesima gravità in spezie, si muovono con pari velocità.

Simp. Il vostro discorso procede benissimo veramente: tuttavia mi par duro a credere che una lagrima di piombo si abbia a muover così veloce come una palla d'artiglieria.

Salv. Voi dovevi dire, un grano di rena come una macina da guado. Io non vorrei, Sig. Simplicio, che voi faceste come molt'altri fanno, che, divertendo il discorso dal principale intento, vi attaccaste a un mio detto che mancasse dal vero quant'è un capello, e che sotto questo capello voleste nasconder un difetto d'un altro, grande quant'una gomona da nave. Aristotele dice: «una palla di ferro di cento libbre, cadendo dall'altezza di cento braccia, arriva in terra prima che una di una libbra sia scesa un sol braccio»; io dico ch'ell'arrivano nell'istesso tempo; voi trovate, nel farne l'esperienza, che la maggiore anticipa due dita la minore, cioè che quando la grande percuote in terra, l'altra ne è lontana due dita: ora vorreste dopo queste due dita appiattare le novantanove braccia di Aristotele, e parlando solo del mio minimo errore, metter sotto silenzio l'altro massimo. Aristotele pronunzia che mobili di diversa gravità nel medesimo mezzo si muovono (per quanto depende dalla gravità) con velocitadi proporzionate a i pesi loro, e l'esemplifica con mobili ne i quali si possa scorgere il puro ed assoluto effetto del peso, lasciando l'altre considerazioni sì delle figure come de i minimi momenti, le quali cose grande alterazione ricevono dal mezzo, che altera il semplice effetto della sola gravità: che perciò si vede l'oro, gravissimo sopra tutte l'altre materie, ridotto in una sottilissima foglia andar vagando per aria; l'istesso fanno i sassi pestati in sottilissima polvere. Ma se voi volete mantenere la proposizione universale, bisogna che voi mostriate, la proporzione delle velocità osservarsi in tutti i gravi, e che un sasso di venti libbre si muova dieci volte più veloce che uno di due; il che vi dico esser falso, e che, cadendo dall'altezza di cinquanta o cento braccia, arrivano in terra nell'istesso momento.

Simp. Forse da grandissime altezze di migliaia di braccia seguirebbe quello che in queste altezze minori non si vede accadere.

Salv. Se Aristotele avesse inteso questo, voi gli addossereste un altro errore, che sarebbe una bugia; perché, non si trovando in terra tali altezze perpendicolari, chiara cosa è che Aristotele non ne poteva aver fatta esperienza: e pur ci vuol persuadere d'averla fatta, mentre dice che tale effetto si vede.

Simp. Aristotele veramente non si serve di questo principio, ma di quell'altro, che non credo che patisca queste difficoltà.

Salv. E l'altro ancora non è men falso di questo; e mi maraviglio che per voi stesso non penetriate la fallacia, e che non v'accorghiate che quando fusse vero che l'istesso mobile in mezzi di differente sottilità e rarità, ed in somma di diversa cedenza, quali, per esempio, son l'acqua e l'aria, si movesse con velocità nell'aria maggiore che nell'acqua secondo la proporzione della rarità dell'aria a quella dell'acqua, ne seguirebbe che ogni mobile che scendesse per aria, scenderebbe anco nell'acqua: il che è tanto falso, quanto che moltissimi corpi scendono nell'aria, che nell'acqua non pur non descendono, ma sormontano all'in su.

Simp. Io non intendo la necessità della vostra consequenza; e più dirò che Aristotele parla di quei mobili gravi che descendono nell'un mezzo e nell'altro, e non di quelli che scendono nell'aria, e nell'acqua vanno all'in su.

Salv. Voi arrecate per il Filosofo di quelle difese che egli assolutamente non produrrebbe, per non aggravar il primo errore. Però ditemi se la corpulenza dell'acqua, o quel che si sia che ritarda il moto, ha qualche proporzione alla corpulenza dell'aria, che meno lo ritarda; ed avendola, assegnatela a vostro beneplacito.

Simp. Halla, e ponghiamo ch'ella sia in proporzione decupla; e che però la velocità di un grave che descenda in amendue gli elementi, sarà dieci volte più tardo nell'acqua che nell'aria.

Salv. Piglio adesso un di quei gravi che vanno in giù nell'aria, ma nell'acqua no, qual sarebbe una palla di legno, e vi domando che voi gli assegniate qual velocità più vi piace, mentre scende per aria.

Simp. Ponghiamo che ella si muova con venti gradi di velocità.

Salv. Benissimo. Ed è manifesto che tal velocità a qualche altra minore può avere la medesima proporzione che la corpulenza dell'acqua a quella dell'aria, e che questa sarà la velocità di due soli gradi; tal che veramente, a filo e a dirittura, conforme all'assunto d'Aristotele, si doverebbe concludere che la palla di legno, che nell'aria, dieci volte più cedente dell'acqua, si muove scendendo con venti gradi di velocità, nell'acqua dovrebbe scendere con due, e non venir a galla dal fondo, come fa: se già voi non voleste dire che nell'acqua il venir ad alto, nel legno, sia l'istesso che 'l calare a basso con due gradi di velocità; il che non credo. Ma già che la palla del legno non cala al fondo, credo pure che mi concederete che qualche altra palla d'altra materia, diversa dal legno, si potrebbe trovare, che nell'acqua scendesse con due gradi di velocità.

Simp. Potrebbesi senza dubbio, ma di materia notabilmente più grave del legno.

Salv. Questo è quel ch'io vo cercando. Ma questa seconda palla, che nell'acqua descende con due gradi di velocità, con quanta velocità descenderà nell'aria? Bisogna (se volete servar la regola d'Aristotele) che rispondiate che si moverà con venti gradi: ma venti gradi di velocità avete voi medesimo assegnati alla palla di legno: adunque questa e l'altra assai più grave si moveranno per l'aria con egual velocità. Or come accorda il Filosofo questa conclusione con l'altra sua, che i mobili di diversa gravità nel medesimo mezzo si muovano con diverse velocità, e diverse tanto quanto le gravità loro? Ma senza molto profonde contemplazioni, come avete voi fatto a non osservar accidenti frequentissimi e palpabilissimi, e non badare a due corpi che nell'acqua si moveranno l'uno cento volte più velocemente dell'altro, ma che nell'aria poi quel più veloce non supererà l'altro di un sol centesimo? come, per esempio, un uovo di marmo scenderà nell'acqua cento volte più presto che alcuno di gallina, che per l'aria nell'altezza di venti braccia non l'anticiperà di quattro dita; ed in somma tal grave andrà al fondo in tre ore in dieci braccia d'acqua, che in aria le passerà in una battuta o due di polso, e tale (come sarebbe una palla di piombo) le passerà in tempo facilmente men che doppio. E qui so ben, Sig. Simplicio, che voi comprendete che non ci ha luogo distinzione o risposta veruna. Concludiamo per tanto, che tale argomento non conclude nulla contro al vacuo; e quando concludesse, distruggerebbe solamente gli spazii notabilmente grandi, quali né io né credo che quelli antichi supponessero naturalmente darsi, se ben forse con violenza si possan fare, come par che da varie esperienze si raccolga, le quali troppo lungo sarebbe il voler al presente arrecare.

Sagr. Vedendo che il Sig. Simplicio tace, piglierò io campo di dire alcuna cosa. Già che assai apertamente avete dimostrato, come non è altrimenti vero che mobili disegualmente gravi si muovano nel medesimo mezzo con velocità proporzionate alle gravità loro, ma con eguale, intendendo de i gravi dell'istessa materia o vero dell'istessa gravità in specie, ma non già (come credo) di gravità differenti in specie (perché non penso che voi intendiate di concluderci ch'una palla di sughero si muova con pari velocità ch'una di piombo); ed avendo, di più, dimostrato molto chiaramente, come non è vero che 'l medesimo mobile in mezzi di diverse resistenze ritenga nella velocità e tardità sue la medesima proporzione che le resistenze; a me sarebbe cosa gratissima il sentire, quali siano le proporzioni che nell'un caso e nell'altro vengono osservate.

Salv. I quesiti son belli, ed io ci ho molte volte pensato: vi dirò il discorso fattoci attorno, e quello che ne ho in ultimo ritratto. Dopo essermi certificato, non esser vero che il medesimo mobile in mezzi di diversa resistenza osservi nella velocità la proporzione delle cedenze di essi mezzi; né meno che nel medesimo mezzo mobili di diversa gravità ritengano nelle velocità loro la proporzione di esse gravità (intendendo anco delle gravità diverse in specie); cominciai a comporre insieme amendue questi accidenti, avvertendo quello che accadesse de i mobili differenti di gravità posti in mezzi di diverse resistenze: e m'accorsi, le disegualità delle velocità trovarsi tuttavia maggiori ne i mezzi più resistenti che ne i più cedenti, e ciò con diversità tali, che di due mobili che scendendo per aria pochissimo differiranno in velocità di moto, nell'acqua l'uno si moverà dieci volte più veloce dell'altro; anzi che tale che nell'aria velocemente descende, nell'acqua non solo non scenderà, ma resterà del tutto privo di moto, e, quel che è più, si moverà all'in su: perché si potrà tal volta trovare qualche sorte di legno, o qualche nodo o radica di quello, che nell'acqua potrà stare, in quiete, che nell'aria velocemente descenderà.

Sagr. Io più volte mi son messo con una estrema flemma per veder di ridurre una palla di cera, che per se stessa non va a fondo, con l'aggiugnerli grani di rena, a segno tale di gravità simile all'acqua, che nel mezzo di quella si fermasse; né mai, per diligenza usata, mi successe il poterlo conseguire: onde non so se altra materia solida si ritrovi tanto naturalmente simile in gravità all'acqua, che, posta in essa, in ogni luogo potesse fermarsi.

Salv. Sono in questo, come in mille altre operazioni, assai più diligenti molti animali, che non siamo noi altri. E nel vostro caso i pesci vi arebber potuto porger qualche documento, essendo in questo esercizio così dotti, che ad arbitrio loro si equilibrano non solo con un'acqua, ma con differenti notabilmente o per propria natura o per una sopravvenente torbida o per salsedine, che fa differenza assai grande; si equilibrano, dico, tanto esattamente, che senza punto muoversi restano in quiete in ogni luogo; e ciò, per mio credere, fanno eglino servendosi dello strumento datogli dalla natura a cotal fine, cioè di quella vescichetta che hanno in corpo, la quale per uno assai angusto meato risponde alla lor bocca, e per quello a posta loro o mandano fuori parte dell'aria che in dette vesciche si contiene, o, venendo col nuoto a galla, altra ne attraggono, rendendosi con tale arte or più or meno gravi dell'acqua, ed a lor beneplacito equilibrandosegli.

Sagr. Io con un altro artifizio ingannai alcuni amici, appresso i quali mi ero vantato di ridurre quella palla di cera al giusto equilibrio con l'acqua; ed avendo messo nel fondo del vaso una parte di acqua salata, e sopra quella dolce, mostrai loro la palla che a mezz'acqua si fermava, e spinta nel fondo o sospinta ad alto né in questo né in quel sito restava, ma ritornava nel mezzo.

Salv. Non è cotesta esperienza priva di utilità: perché trattandosi da i medici in particolare delle diverse qualità di acque, e tra l'altre principalmente della leggerezza o gravità più di questa che di quella, con una simil palla, aggiustata sì che resti ambigua, per così dire, tra lo scendere e 'l salire in un'acqua, per minima che sia la differenza di peso tra due acque, se, in una, tal palla scenderà, nell'altra, che sia più grave, salirà; ed è talmente esatta cotale esperienza, che la giunta di due grani di sale solamente, che si mettino in sei libbre d'acqua, farà risalire dal fondo alla superficie quella palla che vi era pur allora scesa. E più vi voglio dire, in confermazione dell'esattezza di questa esperienza ed insieme per chiara prova della nulla resistenza dell'acqua all'esser divisa, che non solamente l'ingravirla, con la mistione di qualche materia più grave di lei, induce tanto notabil differenza, ma il riscaldarla o raffreddarla un poco produce il medesimo effetto, e con sì sottile operazione, che l'infonder quattro gocciole d'altra acqua un poco più calda o un poco più fredda delle sei libbre, farà che la palla vi scenda o vi sormonti: vi scenderà infondendovi la calda, e monterà per l'infusione della fredda. Or vedete quanto s'ingannino quei filosofi che voglion metter nell'acqua viscosità o altra congiunzione di parti, che la facciano resistente alla divisione e penetrazione.

Sagr. Veddi molto concludenti discorsi intorno a questo argomento in un trattato del nostro Accademico: tuttavia mi resta un gagliardo scrupolo, il quale non so rimuovere; perché se nulla di tenacità e coerenza risiede tra le parti dell'acqua, come possono sostenersi assai grandi pezzi e molto rilevati, in particolare sopra le foglie de i cavoli, senza spargersi e spianarsi?

Salv. Ancor che vero sia che colui che ha dalla sua la conclusione vera, possa risolvere tutte l'instanze che vengono opposte in contrario, non però mi arrogherei io il poter ciò fare; né la mia impotenza deve denigrare la candidezza della verità. Io, primieramente, vi confesso che non so come vadia il negozio del sostenersi quei globi d'acqua assai rilevati e grandi, se bene io so di certo che da tenacità interna, che sia tra le sue parti, ciò non deriva; onde resta necessario che la cagione di cotal effetto risegga fuori. Che ella non sia interna, oltre all'esperienze mostrate ve lo posso confermare con un'altra efficacissima. Se le parti di quell'acqua che, rilevata, si sostiene mentre è circondata dall'aria, avessero cagione interna per ciò fare, molto più si sosterrebbono circondate che fussero da un mezzo nel quale avessero minor propensione di descendere che nell'aria ambiente non hanno: ma un mezzo tale sarebbe ogni fluido più grave dell'aria, come, v. g., il vino; e però infondendo intorno a quel globo d'acqua del vino, se gli potrebbe alzare intorno intorno, senza che le parti dell'acqua, conglutinate dall'interna viscosità, si dissolvessero: ma ciò non accad'egli; anzi non prima se gli accosterà il liquore sparsogli intorno, che, senza aspettar che molto se gli elevi intorno, si dissolverà e spianerà, restandogli di sotto, se sarà vino rosso: è dunque esterna, e forse dell'aria ambiente, la cagione di tale effetto. E veramente si osserva una gran dissensione tra l'aria e l'acqua, la quale ho io in un'altra esperienza osservata; e questa è, che s'io empio d'acqua una palla di cristallo, che abbia un foro angusto quant'è la grossezza d'un fil di paglia, e così piena la volto con la bocca all'in giù, non però l'acqua, benché gravissima e pronta a scender per aria, e l'aria, altrettanto disposta a salire, come leggerissima, per l'acqua, si accordano, quella a scendere uscendo per il foro, e questa a salire entrandovi, ma restano amendue ritrose e contumaci; all'incontro poi, se io presenterò a quel foro un vaso con del vino rosso, che quasi insensibilmente è men grave dell'acqua, lo vedremo subito con tratti rosseggianti lentamente ascendere per mezzo l'acqua, e l'acqua con pari tardità scender per il vino, senza punto mescolarsi, sin che finalmente la palla si empirà tutta di vino e l'acqua calerà tutta nel fondo del vaso di sotto. Or che si deve qui dire o che argumentarne, fuor che una disconvenienza tra l'acqua e l'aria, occulta a me, ma forse...

Simp. Mi vien quasi da ridere nel veder la grande antipatia che ha il Sig. Salviati con l'antipatia, che né pur vuol nominarla; e pur è tanto accommodata a scior la difficoltà.

Salv. Or sia questa, in grazia del Sig. Simplicio, la soluzione del nostro dubbio: e lasciato il digredire, torniamo al nostro proposito. Veduto come la differenza di velocità, ne i mobili di gravità diverse, si trova esser sommamente maggiore ne i mezzi più e più resistenti; ma che più? nel mezzo dell'argento vivo l'oro non solamente va in fondo più velocemente del piombo, ma esso solo vi descende, e gli altri metalli e pietre tutti vi si muovono in su e vi galleggiano, dove che tra palle d'oro, di piombo, di rame, di porfido, o di altre materie gravi, quasi del tutto insensibile sarà la disegualità del moto per aria, ché sicuramente una palla d'oro nel fine della scesa di cento braccia non preverrà una di rame di quattro dita; veduto, dico, questo, cascai in opinione che se si levasse totalmente la resistenza del mezzo, tutte le materie descenderebbero con eguali velocità.

Simp. Gran detto è questo, Sig. Salviati. Io non crederò mai che nell'istesso vacuo, se pur vi si desse il moto, un fiocco di lana si movesse così veloce come un pezzo di piombo.

Salv. Pian piano, Sig. Simplicio: la vostra difficoltà non è tanto recondita, né io così inavveduto, che si debba credere che non mi sia sovvenuta, e che in consequenza io non vi abbia trovato ripiego. Però, per mia dichiarazione e vostra intelligenza, sentite il mio discorso. Noi siamo su 'l volere investigare quello che accaderebbe a i mobili differentissimi di peso in un mezzo dove la resistenza sua fusse nulla, sì che tutta la differenza di velocità, che tra essi mobili si ritrovasse, referir si dovesse alla sola disuguaglianza di peso; e perché solo uno spazio del tutto voto d'aria e di ogni altro corpo, ancor che tenue e cedente, sarebbe atto a sensatamente mostrarci quello che ricerchiamo, già che manchiamo di cotale spazio, andremo osservando ciò che accaggia ne i mezzi più sottili e meno resistenti, in comparazione di quello che si vede accadere ne gli altri manco sottili e più resistenti: ché se noi troveremo, in fatto, i mobili differenti di gravità meno e meno differir di velocità secondo che in mezzi più e più cedenti si troveranno e che finalmente, ancor che estremamente diseguali di peso, nel mezzo più d'ogni altro tenue, se ben non voto, piccolissima si scorga e quasi inosservabile la diversità della velocità, parmi che ben potremo con molto probabil coniettura credere che nel vacuo sarebbero le velocità loro del tutto eguali. Per tanto consideriamo ciò che accade nell'aria: dove, per aver una figura di superficie ben terminata e di materia leggierissima, voglio che pigliamo una vescica gonfiata, nella quale l'aria che vi sarà dentro peserà, nel mezzo dell'aria stessa, niente o poco, perché poco vi si potrà comprimere; talché la gravità è solo quella poca della stessa pellicola, che non sarebbe la millesima parte del peso d'una mole di piombo grande quanto la medesima vescica gonfiata. Queste, Sig. Simplicio, lasciate dall'altezza di quattro o sei braccia, di quanto spazio stimereste che 'l piombo fusse per anticipare la vescica nella sua scesa? siate sicuro che non l'anticiperebbe del triplo, né anco del doppio, se ben già l'aresti fatto mille volte più veloce.

Simp. Potrebbe esser che nel principio del moto, cioè nelle prime quattro o sei braccia, accadesse cotesto che dite: ma nel progresso ed in una lunga continuazione, credo che 'l piombo se la lascerebbe indietro non solamente delle dodici parti dello spazio le sei, ma anco le otto e le dieci.

Salv. Ed io ancora credo l'istesso, e non dubito che in distanze grandissime potesse il piombo aver passato cento miglia di spazio, prima che la vescica ne avesse passato un solo: ma questo, Sig. Simplicio mio, che voi proponete come effetto contrariante alla mia proposizione, è quello che massimamente la conferma. È (torno a dire) l'intento mio dichiarare, come delle diverse velocità di mobili di differente gravità non ne sia altramente causa la diversa gravità, ma che ciò dependa da accidenti esteriori ed in particolare dalla resistenza del mezzo, sì che, tolta questa, tutti i mobili si moverebber con i medesimi gradi di velocità: e questo deduco io principalmente da quello che ora voi stesso ammettete e che è verissimo, cioè che di mobili differentissimi di peso le velocità più e più differiscono secondo che maggiori e maggiori sono gli spazii che essi van trapassando; effetto che non seguirebbe quando ei dependesse dalle differenti gravità. Imperò che, essendo esse sempre le medesime, medesima dovrebbe mantenersi sempre la proporzione tra gli spazii passati, la qual proporzione noi veggiamo andar, nella continuazion del moto, sempre crescendo; poiché l'un mobile gravissimo nella scesa d'un braccio non anticiperà il leggierissimo della decima parte di tale spazio, ma nella caduta di dodici braccia lo preverrà della terza parte, in quella di cento l'anticiperà di 90/100, etc.

Simp. Tutto bene: ma, seguitando le vostre vestigie, se la differenza di peso in mobili di diversa gravità non può cagionare la mutazion di proporzione nelle velocità loro, atteso che le gravità non si mutano, né anco il mezzo, che sempre si suppone mantenersi l'istesso, potrà cagionar alterazion alcuna nella proporzione delle velocità.

Salv. Voi acutamente fate instanza contro al mio detto, la quale è ben necessario di risolvere. Dico per tanto che un corpo grave ha da natura intrinseco principio di muoversi verso 'l comun centro de i gravi, cioè del nostro globo terrestre, con movimento continuamente accelerato, ed accelerato sempre egualmente, cioè che in tempi eguali si fanno aggiunte eguali di nuovi momenti e gradi di velocità. E questo si deve intender verificarsi tutta volta che si rimovessero tutti gl'impedimenti accidentarii ed esterni, tra i quali uno ve ne ha che noi rimuover non possiamo, che è l'impedimento del mezzo pieno, mentre dal mobile cadente deve esser aperto e lateralmente mosso: al qual moto trasversale il mezzo, benché fluido cedente e quieto, si oppone con resistenza or minore ed or maggiore, secondo che lentamente o velocemente ei deve aprirsi per dar il transito al mobile; il quale, perché, come ho detto, si va per sua natura continuamente accelerando, vien per consequenza ad incontrar continuamente resistenza maggiore nel mezzo, e però ritardamento e diminuzione nell'acquisto di nuovi gradi di velocità, sì che finalmente la velocità perviene a tal segno, e la resistenza del mezzo a tal grandezza, che, bilanciandosi fra loro, levano il più accelerarsi, e riducono il mobile in un moto equabile ed uniforme, nel quale egli continua poi di mantenersi sempre. È dunque, nel mezzo, accrescimento di resistenza, non perché si muti la sua essenza, ma perché si altera la velocità con la quale ei deve aprirsi e lateralmente muoversi per cedere il passaggio al cadente, il quale va successivamente accelerandosi. Ora il vedere che la resistenza dell'aria al poco momento della vescica è grandissima, ed al gran peso del piombo è piccolissima, mi fa tener per fermo che chi la rimovesse del tutto, con l'arrecare alla vescica grandissimo commodo, ma ben poco al piombo, le velocità loro si pareggerebbero. Posto dunque questo principio, che nel mezzo dove, o per esser vacuo o per altro, non fusse resistenza veruna che ostasse alla velocità del moto, sì che di tutti i mobili le velocità fusser pari; potremo assai congruamente assegnar le proporzioni delle velocità di mobili simili e dissimili nell'istesso ed in diversi mezzi pieni, e però resistenti: e ciò conseguiremo col por mente quanto la gravità del mezzo detrae alla gravità del mobile, la qual gravità è lo strumento col quale il mobile si fa strada, rispingendo le parti del mezzo alle bande, operazione che non accade nel mezzo vacuo, e che però differenza nissuna si ha da attendere dalla diversa gravità; e perché è manifesto, il mezzo detrarre alla gravità del corpo da lui contenuto quant'è il peso d'altrettanta della sua materia, scemando con tal proporzione la velocità de i mobili, che nel mezzo non resistente sarebbero (come si è supposto) eguali, aremo l'intento. Come, per esempio, posto che il piombo sia dieci mila volte più grave dell'aria, ma l'ebano mille volte solamente; delle velocità di queste due materie, che, assolutamente prese, cioè rimossa ogni resistenza, sarebbero eguali, l'aria al piombo detrae delli dieci mila gradi uno, ma all'ebano suttrae de' mille gradi uno, o vogliam dire dei dieci mila dieci: quando dunque il piombo e l'ebano scenderanno per aria da qualsivoglia altezza, la quale, rimosso 'l ritardamento dell'aria, avrebbon passata nell'istesso tempo, l'aria alla velocità del piombo detrarrà de i dieci mila gradi uno; ma all'ebano detrae de i decimila dieci; che è quanto a dire, che divisa quella altezza, dalla quale si partono tali mobili, in dieci mila parti, il piombo arriverà in terra restando in dietro l'ebano dieci, anzi pur nove, delle dette dieci mila parti. E che altro è questo, salvo che, cadendo una palla di piombo da una torre alta dugento braccia, trovar che ella anticiperà una d'ebano di manco di quattro dita? Pesa l'ebano mille volte più dell'aria; ma quella vescica così gonfia pesa solamente quattro volte tanto: l'aria, dunque, dalla intrinseca e naturale velocità dell'ebano detrae de' mille gradi uno; ma a quella che pur della vescica assolutamente sarebbe stata l'istessa, l'aria ne toglie delle quattro parti una: allora dunque che la palla d'ebano, cadendo dalla torre, giugnerà in terra, la vescica ne averà passati i tre quarti solamente. Il piombo è più grave dell'acqua dodici volte, ma l'avorio il doppio solamente; l'acqua, dunque, alle assolute velocità loro, che sarebbero eguali, toglie al piombo la duodecima parte, ma all'avorio la metà: nell'acqua adunque, quando il piombo arà sceso undici braccia, l'avorio ne arà scese sei. E discorrendo con tal regola, credo che troveremo, l'esperienze molto più aggiustatamente risponder a cotal computo che a quello d'Aristotele. Con simil progresso troveremo la proporzione tra le velocità del medesimo mobile in diversi mezzi fluidi, paragonando non le diverse resistenze de i mezzi, ma considerando gli eccessi di gravità del mobile sopra le gravità de i mezzi: v. g., lo stagno è mille volte più grave dell'aria, e dieci più dell'acqua; adunque, divisa la velocità assoluta dello stagno in mille gradi, nell'aria, che glie ne detrae la millesima parte, si moverà con gradi novecento novanta nove, ma nell'acqua con novecento solamente, essendo che l'acqua gli detrae solo la decima parte della sua gravità, e l'aria la millesima. Posto un solido poco più grave dell'acqua, qual sarebbe, v. g., il legno di rovere, una palla del quale pesando, diremo, mille dramme, altrettanta acqua ne pesasse novecencinquanta, ma tanta aria ne pesasse due, è manifesto, che posto che la velocità sua assoluta fusse di mille gradi, in aria resterebbe di novecennovant'otto, ma in acqua solamente cinquanta, atteso che l'acqua de i mille gradi di gravità glie ne toglie novecencinquanta, e glie ne lascia solamente cinquanta: tal solido dunque si muoverebbe quasi venti volte più velocemente in aria che in acqua, sì come l'eccesso della gravità sua sopra quella dell'acqua è la vigesima parte della sua propria. E qui voglio che consideriamo, che non potendo muoversi in giù nell'acqua se non materie più gravi in spezie di lei, e, per consequenza, per molte centinaia di volte più gravi dell'aria, nel ricercare qual sia la proporzione delle velocità loro in aria e in acqua, possiamo senza notabile errore far conto che l'aria non detragga cosa di momento dalla assoluta gravità, ed in consequenza dall'assoluta velocità, di tali materie; onde, speditamente trovato l'eccesso della gravità loro sopra la gravità dell'acqua, diremo, la velocità loro per aria alla velocità loro per acqua aver la medesima proporzione che la loro totale gravità all'eccesso di questa sopra la gravità dell'acqua. Per esempio, una palla d'avorio pesa venti once, altrettanta acqua pesa once diciasette; adunque la velocità dell'avorio in aria alla sua velocità in acqua è, prossimamente, come venti a tre.

Sagr. Grandissimo acquisto ho fatto in una materia per se stessa curiosa e nella quale, ma senza profitto, ho molte volte affaticata la mente; né mancherebbe altro, per poter anche praticare queste specolazioni, se non il trovar modo di poter venire in cognizione di quanta sia la gravità dell'aria rispetto all'acqua, ed in consequenza all'altre materie gravi.

Simp. Ma quando si trovasse che l'aria, in vece di gravità, avesse leggerezza, che si dovrebbe dire de gli auti discorsi, per altro molto ingegnosi?

Salv. Converrebbe dire che fussero stati veramente aerei, leggieri e vani. Ma vorrete voi dubitare se l'aria sia grave, mentre avete il testo chiaro d'Aristotele che l'afferma, dicendo che tutti gli elementi, eccetto il fuoco, hanno gravità, anco l'aria stessa? segno di che (soggiugne egli) ne è che l'otro gonfiato pesa più che sgonfiato.

Simp. Che l'otro o pallone gonfiato pesi più, crederei io che procedesse non da gravità che sia nell'aria, ma ne i molti vapori grossi tra essa mescolati in queste nostre regioni basse; mercé de i quali direi io che cresce la gravità dell'otro.

Salv. Non vorrei che lo diceste voi, e molto meno che lo faceste dire ad Aristotele; perché, parlando egli de gli elementi e volendomi persuadere che l'elemento dell'aria è grave, facendomelo veder con l'esperienza, se nel venire alla prova ei mi dicesse: «Piglia un otro e empilo di vapori grossi, ed osserva che il suo peso crescerà», io gli direi che più ancora peserebbe chi l'empiesse di semola; ma soggiugnerei dopo, che tali esperienze provano che le semole ed i vapori grossi son gravi, ma quanto all'elemento dell'aria resterei nel medesimo dubbio di prima. L'esperienza, dunque, di Aristotele è buona, e la proposizion vera. Ma non direi già così di cert'altra ragione, presa pure a signo, di un tal filosofo del quale non mi sovviene il nome, ma so che l'ho letta, il quale argomenta, l'aria esser più grave che leggiera, perché più facilmente porta i gravi all'in giù che i leggieri all'in su.

Sagr. Bene, per mia fé. Adunque, per questa ragione, l'aria sarà molto più grave dell'acqua, avvenga che tutti i gravi son portati più facilmente in giù per aria che per acqua, e tutti i leggieri più agevolmente in questa che in quella; anzi infiniti gravi scendono per l'aria, che nell'acqua ascendono, ed infinite materie salgono per acqua, che per aria calano a basso. Ma sia la gravità dell'otro, Sig. Simplicio, o per i vapori grossi o per l'aria pura, questo niente osta al proposito nostro, che cerchiamo quel che accade a mobili che si muovono in questa nostra regione vaporosa. Però, ritornando a quello che più mi preme, vorrei, per intera ed assoluta instruzzione della presente materia, non solo restare assicurato che l'aria sia (come io tengo per fermo) grave, ma vorrei, se è possibile, saper quanta sia la sua gravità. Però, Sig. Salviati, se avete da sodisfarmi in questo ancora, vi prego a farmene favore.

Salv. Che nell'aria risegga gravità positiva, e non altrimente, come alcuni hanno creduto, leggerezza, la quale forse in veruna materia non si ritrova, assai concludente argomento ce ne porge l'esperienza del pallone gonfiato, posta da Aristotele; perché se qualità di assoluta e positiva leggerezza fusse nell'aria, multiplicata e compressa l'aria, crescerebbe la leggerezza, e 'n consequenza la propensione di andare in su: ma l'esperienza mostra l'opposito. Quanto all'altra domanda, che è del modo d'investigare la sua gravità, io l'ho praticato in cotal maniera. Ho preso un fiasco di vetro assai capace e col collo strozzato, al quale ho applicato un ditale di cuoio, legato bene stretto nella strozzatura del fiasco, avendo in capo al detto ditale inserta e saldamente fermata un'animella da pallone, per la quale con uno schizzatoio ho per forza fatto passar nel fiasco molta quantità d'aria; della quale, perché patisce d'esser assaissimo condensata, se ne può cacciare due e tre altri fiaschi oltre a quella che naturalmente vi capisce. In una esattissima bilancia ho poi pesato molto precisamente tal fiasco con l'aria dentrovi compressa, aggiustando il peso con minuta arena. Aperta poi l'animella e dato l'esito all'aria, violentemente nel vaso contenuta, e rimessolo in bilancia, trovandolo notabilmente alleggerito, sono andato detraendo dal contrappeso tant'arena, salvandola da parte, che la bilancia resti in equilibrio col residuo contrappeso, cioè col fiasco: e qui non è dubbio che 'l peso della rena salvata è quello dell'aria che forzatamente fu messa nel fiasco e che ultimamente n'è uscita. Ma tale esperienza sin qui non mi assicura d'altro, se non che l'aria contenuta violentemente nel vaso pesò quanto la salvata arena; ma quanto resolutamente e determinatamente pesi l'aria rispetto all'acqua o ad altra materia grave, non per ancora so io, né posso sapere, se io non misuro la quantità di quell'aria compressa: ed a questa investigazione bisogna trovar regola, nella quale ho trovato di potere in due maniere procedere. L'una delle quali è di pigliar un altro simil fiasco, pur, come 'l primo, strozzato, alla strozzatura del quale sia strettamente legato un altro ditale, che dall'altra sua testa abbracci l'animella dell'altro, e intorno a quella con saldissimo nodo sia legato. Questo secondo fiasco convien che nel fondo sia forato, in modo che per tal foro si possa mettere uno stile di ferro, con il quale si possa, quando vorremo, aprir la detta animella per dar l'esito alla soverchia aria dell'altro vaso, pesata ch'ella sia: ma deve questo secondo fiasco esser pieno d'acqua. Apparecchiato il tutto nella maniera detta ed aprendo con lo stile l'animella, l'aria, uscendo con impeto e passando nel vaso dell'acqua, la caccerà fuora per il foro del fondo; ed è manifesto, la quantità dell'acqua che in tal guisa verrà cacciata, essere eguale alla mole e quantità d'aria che dall'altro vaso sarà uscita. Salvata dunque tale acqua, e tornato a pesare il vaso alleggerito dell'aria compressa (il quale suppongo che fusse pesato anche prima, con detta aria sforzata), e detratto, al modo già dichiarato, l'arena superflua, è manifesto, questa essere il giusto peso di tanta aria in mole, quanta è la mole dell'acqua scacciata e salvata; la quale peseremo, e vedremo quante volte il peso suo conterrà il peso della serbata arena, e senza errore potremo affermar, tante volte esser più grave l'acqua dell'aria: la quale non sarà dieci volte altrimenti, come par che stimasse Aristotele, ma ben circa quattrocento, come tale esperienza ne mostra. L'altro modo è più speditivo, e puossi fare con un vaso solo, cioè col primo, accomodato nel modo detto; nel quale non voglio che mettiamo altra aria oltre a quella che naturalmente vi si ritrova, ma voglio che vi cacciamo dell'acqua senza lasciare uscir punto di aria, la quale, dovendo cedere alla sopravvenente acqua, è forza che si comprima. Spintavi dunque più acqua che sia possibile, che pure senza molta violenza vi se ne potrà mettere i tre quarti della tenuta del fiasco, mettasi su la bilancia, e diligentissimamente si pesi; il che fatto, tenendo il vaso col collo in su, si apra l'animella, dando l'uscita all'aria, della quale ne scapperà fuora giustamente quanta è l'acqua contenuta nel fiasco. Uscita che sia l'aria, si torni a metter il vaso in bilancia, il quale per la partita dell'aria si troverà alleggerito; e detratto dal contrappeso il peso superfluo, da esso aremo la gravità di tant'aria quanta è l'acqua del fiasco.

Simp. Gli artifizii ritrovati da voi non si può dire che non siano sottili e molto ingegnosi: ma mentre mi pare che in apparenza diano intera sodisfazzione all'intelletto, mi metton per un altro verso in confusione. Imperò che, essendo indubitabilmente vero che gli elementi nelle proprie regioni non sono né leggieri né gravi, non posso intender come e dove quella porzione d'aria che parve pesasse, v. g., quattro dramme di rena, debba poi realmente aver tale gravità nell'aria, nella quale ben la ritiene la rena che la contrappesò; e però mi pare che l'esperienza dovesse esser praticata non nell'elemento dell'aria, ma in un mezzo dove l'aria stessa potesse esercitare il suo talento del peso, se ella veramente ne possiede.

Salv. Acuta certo è l'opposizione del Sig. Simplicio, e però è necessario o che ella sia insolubile o che la soluzione sia non men sottile. Che quell'aria la quale, compressa, mostrò pesare quanto quella rena, posta in libertà nel suo elemento non sia più per pesare, ma sì ben la rena, è cosa chiarissima: e però per far tale esperienza conveniva eleggere un luogo e un mezzo, dove l'aria, non men che la rena, potesse gravitare; perché, come più volte si è detto, il mezzo detrae dal peso d'ogni materia che vi s'immerge, tanto quant'è il peso d'altrettanta parte dell'istesso mezzo, quant'è la mole immersa, sì che l'aria all'aria leva tutta la gravità: l'operazione dunque, acciò fusse fatta esattamente, converrebbe farla nel vacuo, dove ogni grave eserciterebbe il suo momento senza diminuzione alcuna. Quando dunque, Sig. Simplicio, noi pesassimo una porzione d'aria nel vacuo, restereste allora sincerato e assicurato del fatto?

Simp. Veramente sì; ma questo è un desiderare o richieder l'impossibile.

Salv. E però grandissimo converrà che sia l'obbligo che mi dovrete, qual volta per amor vostro io effettui un impossibile. Ma io non voglio vendervi quel che già vi ho donato, perché di già nell'addotta esperienza pesiamo noi l'aria nel vacuo, e non nell'aria o in altro mezzo pieno. Che alla mole, Sig. Simplicio, che nel mezzo fluido s'immerge, venga dall'istesso mezzo detratto della gravità, ciò proviene perché ei resiste all'esser aperto, discacciato e finalmente sollevato; segno di che ne dà la prontezza sua nel ricorrer subito a riempier lo spazio che l'immersa mole in lui occupava, qualunque volta essa ne parta: che quando di tale immersione ei nulla sentisse, niente opererebbe egli contro di quella. Ora ditemi: mentre voi avete in aria il fiasco di già pieno della medesima aria naturalmente contenutavi, qual divisione, scacciamento, o in somma qual mutazione, riceve l'aria esterna ambiente dalla seconda aria che nuovamente s'infonde con forza nel vaso? Forse s'ingrandisce il fiasco, onde l'ambiente debba maggiormente ritirarsi per cedergli luogo? certo no: e però possiam dire che la seconda aria non si immerge nell'ambiente, non vi occupando ella spazio, ma è come se si mettesse nel vacuo; anzi pur vi si mette ella realmente, e si trapone ne i vacui non ben ripieni dalla prima aria non condensata. E veramente non so conoscere differenza nissuna tra due costituzioni d'ambito ed ambiente, mentre in questa l'ambiente niente preme l'ambito, ed in quella l'ambito punto non spinge contr'all'ambiente: e tali sono la locazione di qualche materia nel vacuo e la seconda aria compressa nel fiasco. Il peso, dunque, che si trova in tal aria condensata, è quello che ella arebbe liberamente sparsa nel vacuo. Ben è vero che 'l peso della rena che la contrappesò, come quella che era nell'aria libera, nel vacuo sarebbe stato un poco più del giusto; e però convien dire che l'aria pesata sia veramente alquanto men grave della rena che la contrappesò, cioè tanto quanto peserebbe altrettanta aria nel vacuo.

Simp. Pur mi pareva che nell'addotte esperienze vi fusse qualche cosa da desiderare; ma ora mi quieto interamente.

Salv. Le cose da me sin qui prodotte, ed in particolare questa, che la differenza di gravità, ben che grandissima, non abbia parte veruna nel diversificare le velocità de i mobili, sì che, per quanto da quella depende, tutti si moverebbero con egual celerità, è tanto nuova e, nella prima apprensione, remota dal verisimile, che quando non si avesse modo di dilucidarla e renderla più chiara che 'l Sole, meglio sarebbe il tacerla che 'l pronunziarla; però, già che me la sono lasciata scappar di bocca, convien ch'io non lasci indietro esperienza o ragione che possa corroborarla.

Sagr. Non questa sola, ma molte altre insieme delle vostre proposizioni son così remote dalle opinioni e dottrine communemente ricevute, che spargendosi in publico vi conciterebber numero grande di contradittori, essendo che l'innata condizione de gli uomini non vede con buon occhio che altri nel loro esercizio scuopra verità o falsità non scoperte da loro; e col dar titolo di innovatori di dottrine, poco grato a gli orecchi di molti, s'ingegnano di tagliar quei nodi che non possono sciorre, e con mine sotterranee dissipar quelli edifizii che sono stati, con gli strumenti consueti, da pazienti artefici costrutti. Ma con esso noi, lontani da simili pretensioni, l'esperienze e le ragioni sin qui addotte bastano a quietarci: tuttavia, quando abbiate altre più palpabili esperienze e ragioni più efficaci, le sentiremo molto volentieri.

Salv. L'esperienza fatta con due mobili quanto più si possa differenti di peso, col fargli scendere da un'altezza per osservar se la velocità loro sia eguale, patisce qualche difficoltà: imperò che se l'altezza sarà grande, il mezzo, che dall'impeto del cadente deve esser aperto e lateralmente spinto, di molto maggior pregiudizio sarà al piccol momento del mobile leggierissimo che alla violenza del gravissimo, per lo che per lungo spazio il leggiero rimarrà indietro; e nell'altezza piccola si potrebbe dubitare se veramente non vi fusse differenza, o pur se ve ne fusse, ma inosservabile. E però sono andato pensando di reiterar tante volte la scesa da piccole altezze, ed accumulare insieme tante di quelle minime differenze di tempo, che potessero intercedere tra l'arrivo al termine del grave e l'arrivo del leggiero, che così congiunte facessero un tempo non solo osservabile, ma grandemente osservabile. In oltre, per potermi prevaler di moti quanto si possa tardi, ne i quali manco lavora la resistenza del mezzo in alterar l'effetto che depende dalla semplice gravità, sono andato pensando di fare scendere i mobili sopra un piano declive, non molto elevato sopra l'orizontale; ché sopra questo, non meno che nel perpendicolo, potrà scorgersi quello che facciano i gravi differenti di peso; e passando più avanti, ho anco voluto liberarmi da qualche impedimento che potesse nascer dal contatto di essi mobili su 'l detto piano declive: e finalmente ho preso due palle, una di piombo ed una di sughero, quella ben più di cento volte più grave di questa, e ciascheduna di loro ho attaccata a due sottili spaghetti eguali, lunghi quattro o cinque braccia, legati ad alto; allontanata poi l'una e l'altra palla dallo stato perpendicolare, gli ho dato l'andare nell'istesso momento, ed esse, scendendo per le circonferenze de' cerchi descritti da gli spaghi eguali, lor semidiametri, passate oltre al perpendicolo, son poi per le medesime strade ritornate indietro; e reiterando ben cento volte per lor medesime le andate e le tornate, hanno sensatamente mostrato, come la grave va talmente sotto il tempo della leggiera, che né in ben cento vibrazioni, né in mille, anticipa il tempo d'un minimo momento, ma camminano con passo egualissimo. Scorgesi anco l'operazione del mezzo, il quale, arrecando qualche impedimento al moto, assai più diminuisce le vibrazioni del sughero che quelle del piombo, ma non però che le renda più o men frequenti; anzi quando gli archi passati dal sughero non fusser più che di cinque o sei gradi, e quei del piombo di cinquanta o sessanta, son eglin passati sotto i medesimi tempi.

Simp. Se questo è, come dunque non sarà la velocità del piombo maggiore della velocità del sughero, facendo quello sessanta gradi di viaggio nel tempo che questo ne passa appena sei?

Salv. Ma che direste, Sig. Simplicio, quando amendue spedissero nell'istesso tempo i lor viaggi, mentre il sughero, allontanato dal perpendicolo trenta gradi, avesse a passar l'arco di sessanta, e 'l piombo, slargato dal medesimo punto di mezzo due soli gradi, scorresse l'arco di quattro? non sarebbe allora altrettanto più veloce il sughero? e pur l'esperienza mostra ciò avvenire. Però notate: slargato il pendolo del piombo, v. g., cinquanta gradi dal perpendicolo e di lì lasciato in libertà, scorre, e passando oltre al perpendicolo quasi altri cinquanta, descrive l'arco di quasi cento gradi e ritornando per se stesso indietro, descrive un altro poco minore arco, e continuando le sue vibrazioni, dopo gran numero di quelle si riduce finalmente alla quiete. Ciascheduna di tali vibrazioni si fa sotto tempi eguali, tanto quella di novanta gradi, quanto quella di cinquanta, di venti, di dieci e di quattro; sì che, in conseguenza, la velocità del mobile vien sempre languendo, poiché sotto tempi eguali va passando successivamente archi sempre minori e minori. Un simile, anzi l'istesso, effetto fa il sughero pendente da un filo altrettanto lungo, salvo che in minor numero di vibrazioni si conduce alla quiete, come meno atto, mediante la sua leggerezza, a superar l'ostacolo dell'aria: con tutto ciò tutte le vibrazioni, grandi e piccole, si fanno sotto tempi eguali tra di loro, ed eguali ancora a i tempi delle vibrazioni del piombo. Onde è vero che, se mentre il piombo passa un arco di cinquanta gradi, il sughero ne passa uno di dieci, il sughero allora è più tardo del piombo; ma accaderà ancora, all'incontro, che il sughero passi l'arco di cinquanta, quando il piombo passi quel di dieci o di sei: e così, in diversi tempi, or sarà più veloce il piombo ed ora il sughero. Ma se gli stessi mobili passeranno ancora, sotto i medesimi tempi eguali, archi eguali, ben sicuramente si potrà dire allora essere le velocità loro eguali.

Simp. Mi pare e non mi pare che questo discorso sia concludente, e mi sento nella mente una tal confusione, che mi nasce dal muoversi, e l'uno e l'altro mobile, or veloce or tardo ed or tardissimo, che non mi lascia ridurre in chiaro come vero sia che le velocità loro sian sempre eguali.

Sagr. Concedami in grazia, Sig. Salviati, che io dica due parole. E ditemi, Sig. Simplicio, se voi ammettete che dir si possa con assoluta verità, le velocità del sughero e del piombo essere eguali ogni volta che, partendosi amendue nell'istesso momento dalla quiete e movendosi per le medesime inclinazioni, passassero sempre spazii eguali in tempi eguali?

Simp. In questo non si può dubitare, né se gli può contradire.

Sagr. Accade ora ne i pendoli, che ciaschedun di loro passi or sessanta gradi, or cinquanta, or trenta, or dieci, or otto, or quattro, or due, etc.; e quando amendue passano l'arco di sessanta gradi, lo passano nell'istesso tempo; nell'arco di cinquanta, metton l'istesso tempo l'uno che l'altro mobile; così nell'arco di trenta, di dieci, e ne gli altri: e però si conclude, che la velocità del piombo nell'arco di sessanta gradi è eguale alla velocità del sughero nell'arco medesimo di sessanta, e che le velocità nell'arco di cinquanta son pur tra loro eguali, e così ne gli altri. Ma non si dice già che la velocità che si esercita nell'arco di sessanta, sia eguale alla velocità che si esercita nell'arco di cinquanta, né questa a quella dell'arco di trenta, etc.; ma son sempre minori le velocità ne gli archi minori: il che si raccoglie dal veder noi sensatamente, il medesimo mobile metter tanto tempo nel passar l'arco grande de i sessanta gradi, quanto nel passare il minor di cinquanta o 'l minimo di dieci, ed in somma nell'esser passati tutti sempre sotto tempi eguali. È vero dunque che ben vanno, e 'l piombo e 'l sughero, ritardando il moto secondo la diminuzione de gli archi, ma non però alterano la concordia loro nel mantener l'egualità della velocità in tutti i medesimi archi da loro passati. Ho voluto dir questo più per sentire se ho ben capito il concetto del Sig. Salviati, che per bisogno ch'io credessi che avesse il Sig. Simplicio di più chiara esplicazione di quella del Sig. Salviati, che è, come in tutte le sue cose, lucidissima, e tale che, sciogliendo egli il più delle volte questioni non solo in apparenza oscure, ma repugnanti alla natura ed al vero, con ragioni o osservazioni o esperienze tritissime e familiari ad ogn'uno, ha (come da diversi ho inteso) dato occasione a tal uno de i professori più stimati di far minor conto delle sue novità, tenendole come a vile, per dependere da troppo bassi e popolari fondamenti; quasi che la più ammirabile e più da stimarsi condizione delle scienze dimostrative non sia lo scaturire e pullulare da principii notissimi, intesi e conceduti da tutti. Ma seguitiamo pur noi d'andarci pascendo di questi cibi leggieri: e posto che il Sig. Simplicio sia restato appagato nell'intender ed ammettere come l'interna gravità de i diversi mobili non abbia parte alcuna nel diversificar le velocità loro, sì che tutti, per quanto da quella depende, si moverebber con l'istesse velocitadi, diteci, Sig. Salviati, in quello che voi riponete le sensate ed apparenti disegualità di moto, e rispondete a quell'instanza che oppone il Sig. Simplicio, e ch'io parimente confermo, dico del vedersi una palla d'artiglieria muoversi più velocemente d'una migliarola di piombo; ché poca sarà la differenza di velocità rispetto a quella che v'oppongo io, di mobili dell'istessa materia, de i quali alcuni de i maggiori scenderanno in meno d'una battuta di polso, in un mezzo, quello spazio che altri minori non lo passeranno in un'ora, né in quattro, né in venti; quali sono le pietre e la minuta rena, e massime quella sottilissima che intorbida l'acqua, nel qual mezzo in molte ore non scende per due braccia, che pietruzze, né molto più grandi, passano in una battuta di polso.

Salv. Quel che operi il mezzo nel ritardar più i mobili, secondo che tra di loro sono in spezie men gravi, già si è dichiarato, mostrando ciò accadere dalla suttrazione di peso: ma come il medesimo mezzo possa con sì gran differenza scemar la velocità ne i mobili differenti solo in grandezza, ancor che siano della medesima materia e dell'istessa figura, ricerca per sua dichiarazione discorso più sottile di quello che basta per intender come la figura del mobile più dilatata, o 'l moto del mezzo che sia fatto contro al mobile, ritarda la velocità di quello. Io del presente problema riduco la cagione alla scabrosità e porosità, che comunemente, e per lo più necessariamente, si ritrova nelle superficie de i corpi solidi, le quali scabrosità nel moto di essi vanno urtando nell'aria o altro mezzo ambiente: di che segno evidente ce ne porge il sentir noi ronzar i corpi, ancor che quanto più si possa rotondati, mentre velocissimamente scorrono per l'aria; e non solo ronzare, ma sibilare e fischiar si sentono, se qualche più notabil cavità o prominenza sarà in essi. Vedesi anco nel girar sopra 'l torno ogni solido rotondo far un poco di vento. Ma che più? non sentiam noi notabil ronzio, ed in tuono molto acuto, farsi dalla trottola, mentre per terra con somma celerità va girando? l'acutezza del qual sibilo si va ingravendo secondo che la velocità della vertigine va di grado in grado languendo: argomento parimente necessario de gl'intoppi nell'aria delle scabrosità, ben che minime, delle superficie loro. Queste non si può dubitare che, nello scendere i mobili, soffregandosi con l'ambiente fluido, apporteranno ritardamento alla velocità, e tanto maggiore quanto la superficie sarà più grande, quale è quella de i solidi minori paragonati a i maggiori.

Simp. Fermate, in grazia, perché qui comincio a confondermi. Imperò che, se bene io intendo ed ammetto che la confricazione del mezzo con la superficie del mobile ritardi il moto, e che più lo ritardi dove, ceteris paribus, la superficie sia maggiore, non capisco però con qual fondamento voi chiamiate maggiore la superficie de i solidi minori; ed oltre a ciò, se, come voi affermate, la maggior superficie deve arrecar maggior ritardamento, i solidi maggiori devriano esser più tardi, il che non è. Ma questa instanza facilmente si toglie con dire, che se bene il maggiore ha maggior superficie, ha anco maggior gravità, contro la quale l'impedimento della maggior superficie non ha a prevalere all'impedimento della superficie minore contro alla minor gravità, sì che la velocità del solido maggiore ne divenga minore. E però non veggo ragione per la quale si debba alterare l'egualità delle velocità, mentre che, quanto si diminuisce la gravità movente, altrettanto si diminuisce la facoltà della superficie ritardante.

Salv. Risolverò congiuntamente tutto quello che opponete. Per tanto voi, Sig. Simplicio, senza controversia ammettete, che quando di due mobili eguali, della stessa materia e simili di figura (i quali indubitabilmente si moverebber egualmente veloci), all'uno di loro si diminuisse tanto la gravità quanto la superficie (ritenendo però la similitudine della figura), non perciò si scemerebbe la velocità nel rimpiccolito.

Simp. Veramente parmi che così dovrebbe seguire, stando però nella vostra dottrina, che vuol che la maggiore o minor gravità non abbia azzione nell'accelerare o ritardar il moto.

Salv. E questo confermo io, e vi ammetto anco 'l vostro detto, dal qual mi par che in consequenza si ritragga, che quando la gravità si diminuisse più che la superficie, nel mobile in tal maniera diminuito si introdurrebbe qualche ritardamento di moto, e maggiore e maggiore quanto a proporzione maggior fusse la diminuzion del peso che la diminuzion della superficie.

Simp. In ciò non ho io repugnanza veruna.

Salv. Or sappiate, Sig. Simplicio, che non si può ne i solidi diminuir tanto la superficie quanto 'l peso, mantenendo la similitudine delle figure. Imperò che, essendo manifesto che nel diminuir un solido grave tanto scema il suo peso quanto la mole, ogni volta che la mole venisse sempre diminuita più che la superficie (nel conservarsi massime la similitudine di figura), la gravità ancora più che la superficie verrebbe diminuita. Ma la geometria c'insegna che molto maggior proporzione è tra la mole e la mole, ne i solidi simili, che tra le loro superficie: il che per vostra maggiore intelligenza vi esplicherò in qualche caso particolare. Però figuratevi, per esempio, un dado, un lato del quale sia, v. g., lungo due dita, sì che una delle sue faccie sarà quattro dita quadre, e tutte e sei, cioè tutta la sua superficie, venti quattro dita quadre; intendete poi, il medesimo dado esser con tre tagli segato in otto piccoli dadi: il lato di ciascun de' quali sarà un dito, e una sua faccia un dito quadro, e tutta la sua superficie sei dita quadre, delle quali l'intero dado ne conteneva venti quattro in superficie. Or vedete come la superficie del piccol dado è la quarta parte della superficie del grande (che tanto è sei di venti quattro); ma l'istesso dado solido è solamente l'ottava; molto più dunque cala la mole, ed in consequenza il peso, che la superficie. E se voi suddividerete il piccol dado in altri otto, aremo per l'intera superficie di un di questi un dito e mezzo quadro, che è la sedicesima parte della superficie del primo dado; ma la sua mole è solamente la sessantaquattresima. Vedete per tanto come in queste sole due divisioni le moli scemano quattro volte più che le loro superficie; e se noi andremo seguitando la suddivisione sino che si riduca il primo solido in una minuta polvere, troveremo la gravità dei minimi atomi diminuita centinaia e centinaia di volte più che le loro superficie. E questo, che vi ho esemplificato ne i cubi, accade in tutti i solidi tra di loro simili, le moli de i quali sono in sesquialtera proporzione delle lor superficie. Vedete dunque con quanto maggior proporzione cresce l'impedimento del contatto della superficie del mobile col mezzo ne i mobili piccoli che ne i maggiori; e se noi aggiugneremo che le scabrosità nelle superficie piccolissime delle polveri sottili non son forse minori di quelle delle superficie de i solidi maggiori che siano con diligenza puliti, guardate quanto bisognerà che 'l mezzo sia fluido e privo onninamente di resistenza all'esser aperto, per dover cedere il passo a così debil virtù. E in tanto notate, Sig. Simplicio, ch'io non equivocai quando poco fa dissi, la superficie de' solidi minori esser più grande in comparazione di quella de i maggiori.

Simp. Io resto interamente appagato: e mi credano certo che se io avessi a ricominciare i miei studii, vorrei seguire il consiglio di Platone e cominciarmi dalle matematiche, le quali veggo che procedono molto scrupolosamente, né vogliono ammetter per sicuro fuor che quello che concludentemente dimostrano.

Sagr. Ho auto gusto grande di questo discorso; ma prima che passiamo più avanti, arei caro di restar capace d'un termine che mi giunse nuovo, quando pur ora diceste che i solidi simili son tra di loro in sesquialtera proporzione delle lor superficie: perché ho ben veduto e inteso la proposizione, con la sua dimostrazione, nella quale si prova, la superficie de' solidi simili esser in duplicata proporzione de i lor lati, e l'altra che prova, i medesimi solidi esser in tripla proporzione de i medesimi lati; ma la proporzione de i solidi con le lor superficie non mi sovvien né anco di averla sentita nominare.

Salv. V. S. medesima da per sé si risponde, e dichiara il dubbio. Imperò che quello che è triplo d'una cosa, della quale un altro è doppio, non vien egli ad esser sesquialtero di questo doppio? certo sì. Or se le superficie sono in doppia proporzione delle linee, delle quali i solidi sono proporzione tripla, non possiam noi dire, i solidi essere in sesquialtera proporzion delle superficie?

Sagr. Ho inteso benissimo. E se bene alcuni altri particolari, attenenti alla materia di cui si tratta, mi resterebbero da domandare, tuttavia, quando ce n'andassimo così di digressione in digressione, tardi verremmo alle quistioni principalmente intese, che appartengono alle diversità de gli accidenti delle resistenze de i solidi all'esser spezzati: e però, quando così piaccia loro, potremo ritornare su 'l primo filo, che si propose da principio.

Salv. V. S. dice molto bene: ma le cose tante e tanto varie che si sono esaminate, ci han rubato tanto tempo, che poco ce n'avanzerà per questo giorno da spendere nell'altro nostro principal argomento, che è pieno di dimostrazioni geometriche, da esser con attenzione considerate; onde stimerei che fusse meglio differire il congresso a dimane, sì per questo che ho detto, come ancora perché potrei portar meco alcuni fogli, dove ho per ordine notati i teoremi e problemi ne i quali si propongono e dimostrano le diverse passioni di tal soggetto, che forse alla memoria, col necessario metodo, non mi sovverrebbero.

Sagr. Io molto bene mi accomodo a questo consiglio, e tanto più volentieri, quanto che, per finire la sessione odierna, arò tempo di sentir la dichiarazione d'alcuni dubbi che mi restavano nella materia che ultimamente trattavamo. De i quali uno è, se si deve stimare che l'impedimento del mezzo possa esser bastante a por termine all'accelerazione a' corpi di materia gravissima, e grandissimi di mole, e di figura sferica; e dico sferica, per pigliar quella che è contenuta sotto la minima superficie, e però meno soggetta al ritardamento. Un altro sarà circa le vibrazioni de i pendoli, e questo ha più capi: l'uno è, se tutte, e grandi e mediocri e minime, si fanno veramente e precisamente sotto tempi eguali; ed un altro, qual sia la proporzione de i tempi de i mobili appesi a fili diseguali, de i tempi, dico, delle lor vibrazioni.

Salv. I quesiti son belli, e, sì come avviene di tutti i veri, dubito che trattandosi di qualsisia di loro, si tirerà dietro tante altre vere e curiose consequenze, che non so se l'avanzo di questo giorno ci basterà per discuterle tutte.

Sagr. S'elle saranno del sapore delle passate, più grato mi sarebbe l'impiegarvi tanti giorni, non che tante ore, quante restano sino a notte; e credo che il Sig. Simplicio non si ristuccherà di tali ragionamenti.

Simp. Sicuramente no, e massime quando si trattano quistioni naturali intorno alle quali non si leggono opinioni o discorsi d'altri filosofi.

Salv. Vengo dunque alla prima, affermando senza veruna dubitazione, non essere sfera sì grande, né di materia sì grave, che la renitenza del mezzo, ancor che tenuissimo, non raffreni la sua accelerazione, e che nella continuazion del moto non lo riduca all'equabilità: di che possiamo ritrar molto chiaro argomento dall'esperienza stessa. Imperò che, se alcun mobile cadente fusse abile, nella sua continuazion di moto, ad acquistar qualsivoglia grado di velocità, nissuna velocità che da motore esterno gli fusse conferita, potrebbe esser così grande, che egli la recusasse e se ne spogliasse mercé dell'impedimento del mezzo; e così una palla d'artiglieria che fusse scesa per aria, v. g., quattro braccia, ed avesse, per esempio, acquistato dieci gradi di velocità, e che con questi entrasse nell'acqua, quando l'impedimento dell'acqua non fusse potente a vietare alla palla un tale impeto, ella l'accrescerebbe, o almeno lo continuerebbe sino al fondo: il che non si vede seguire: anzi l'acqua, benché non fusse più che poche braccia profonda, l'impedisce e debilita in modo, che leggerissima percossa farà nel letto del fiume o del lago. È dunque manifesto, che quella velocità della quale l'acqua l'ha potuta spogliare in un brevissimo viaggio, non glie la lascerebbe già mai acquistare anco nella profondità di mille braccia. E perché permettergli 'l guadagnarsela in mille, per levargliela poi in quattro braccia? Ma che più? non si ved'egli, l'immenso impeto della palla, cacciata dall'istessa artiglieria, esser talmente rintuzzato dall'interposizione di pochissime braccia d'acqua, che senza veruna offesa della nave appena si conduce a percuoterla? L'aria ancora, benché cedentissima, pur reprime la velocità del mobile cadente, ancor che molto grave, come possiamo con simili esperienze comprendere: perché se dalla cima d'una torre molto alta tireremo un'archibusata in giù, questa farà minor botta in terra, che se scaricheremo l'archibuso, alto dal piano solamente quattro o sei braccia; segno evidente che l'impeto con che la palla uscì della canna, scaricata nella sommità della torre, andò diminuendosi nello scender per aria. Adunque lo scender da qualunque grandissima altezza non basterà per fargli acquistare quell'impeto, del quale la resistenza dell'aria la priva quando già in qualsivoglia modo gli sia stato conferito. La rovina parimente che farà in una muraglia un colpo d'una palla cacciata da una colubrina dalla lontananza di venti braccia, non credo che la facesse venendo a perpendicolo da qualsivoglia altezza immensa. Stimo per tanto, esser termine all'accelerazione di qualsivoglia mobile naturale che dalla quiete si parta, e che l'impedimento del mezzo finalmente lo riduca all'egualità, nella quale ben poi sempre si mantenga.

Sagr. L'esperienze veramente mi par che siano molto a proposito; né ci è altro se non che l'avversario potrebbe farsi forte col negar che si debbano verificar nelle moli grandissime e gravissime, e che una palla d'artiglieria venendo dal concavo della Luna, o anco dalla suprema region dell'aria, farebbe percossa maggiore che uscita dal cannone.

Salv. Non è dubbio che molte cose si posson opporre, e che non tutte si possono con esperienze redarguire: tuttavia in questa contradizzione, alcuna cosa par che si possa metter in considerazione, cioè che molto ha del verisimile che 'l grave cadente da un'altezza acquisti tanto d'impeto nell'arrivar in terra, quanto fusse bastante a tirarlo a quell'altezza; come chiaramente si vede in un pendolo assai grave, che slargato cinquanta o sessanta gradi dal perpendicolo, guadagna quella velocità e virtù che basta precisamente a sospignerlo ad altrettanta elevazione, trattone però quel poco che gli vien tolto dall'impedimento dell'aria. Per costituir dunque la palla dell'artiglieria in tanta altezza che bastasse per l'acquisto del pezzo, dovrebbe bastar il tirarla in su a perpendicolo con l'istessa artiglieria, osservando poi se nella ricaduta ella facesse colpo eguale a quello della percossa fatta da vicino nell'uscire; che credo veramente che non sarebbe, a gran segno, tanto gagliardo: e però stimo che la velocità che ha la palla vicino all'uscita del pezzo, sarebbe di quelle che l'impedimento dell'aria non gli lascerebbe conseguire già mai mentre con moto naturale scendesse, partendosi dalla quiete, da qualsivoglia grand'altezza.

Vengo ora a gli altri quesiti, attenenti a i pendoli, materia che a molti parrebbe assai arida, e massime a quei filosofi che stanno continuamente occupati nelle più profonde quistioni delle cose naturali; tuttavia non gli voglio disprezzare, inanimito dall'esempio d'Aristotele medesimo, nel quale io ammiro sopra tutte le cose il non aver egli lasciato, si può dir, materia alcuna, degna in qualche modo di considerazione, che e' non l'abbia toccata. Ed ora, mosso da i quesiti di V. S., penso che potrò dirvi qualche mio pensiero sopra alcuni problemi attenenti alla musica, materia nobilissima, della quale hanno scritto tanti grand'uomini e l'istesso Aristotele, e circa di essa considerar molti problemi curiosi; talché se io ancora da così facili e sensate esperienze trarrò ragioni di accidenti maravigliosi in materia de i suoni, posso sperare che i miei ragionamenti siano per esser graditi da voi.

Sagr. Non solamente graditi, ma da me in particolare sommamente desiderati, come quello che, sendomi dilettato di tutti gli strumenti musici, ed assai filosofato intorno alle consonanze, son sempre restato incapace e perplesso onde avvenga che più mi piaccia e diletti questa che quella, e che alcuna non solo non mi diletti, ma sommamente m'offenda. Il problema poi trito delle due corde tese all'unisono, che al suono dell'una l'altra si muova e attualmente risuoni, mi resta ancora irresoluto, come anco non ben chiare le forme delle consonanze ed altre particolarità.

Salv. Vedremo se da questi nostri pendoli si possa cavare qualche sodisfazione a tutte queste difficoltà. E quanto al primo dubbio, che è, se veramente e puntualissimamente l'istesso pendolo fa tutte le sue vibrazioni, massime, mediocri e minime, sotto tempi precisamente eguali, io mi rimetto a quello che intesi già dal nostro Accademico; il quale dimostra bene, che 'l mobile che descendesse per le corde suttese a qualsivoglia arco, le passerebbe necessariamente tutte in tempi eguali, tanto la suttesa sotto cent'ottanta gradi (cioè tutto il diametro), quanto le suttese di cento, di sessanta, di dieci, di due, di mezzo e di quattro minuti, intendendo che tutte vadano a terminar nell'infimo punto, toccante il piano orizontale. Circa poi i descendenti per gli archi delle medesime corde elevati sopra l'orizonte, e che non siano maggiori d'una quarta, cioè di novanta gradi, mostra parimente l'esperienza, passarsi tutti in tempi eguali, ma però più brevi de i tempi de' passaggi per le corde; effetto che in tanto ha del maraviglioso, in quanto nella prima apprensione par che dovrebbe seguire il contrario: imperò che, sendo comuni i termini del principio e del fine del moto, ed essendo la linea retta la brevissima che tra i medesimi termini si comprende, par ragionevole che il moto fatto per lei s'avesse a spedire nel più breve tempo; il che poi non è, ma il tempo brevissimo, ed in consequenza il moto velocissimo, è quello che si fa per l'arco del quale essa linea retta è corda. Quanto poi alla proporzione de i tempi delle vibrazioni di mobili pendenti da fila di differente lunghezza, sono essi tempi in proporzione suddupla delle lunghezze delle fila, o vogliam dire le lunghezze esser in duplicata proporzion de i tempi, cioè son come i quadrati de i tempi: sì che volendo, v. g., che 'l tempo d'una vibrazione d'un pendolo sia doppio del tempo d'una vibrazione d'un altro, bisogna che la lunghezza della corda di quello sia quadrupla della lunghezza della corda di questo; ed allora, nel tempo d'una vibrazione di quello, un altro ne farà tre, quando la corda di quello sarà nove volte più lunga dell'altra: dal che ne séguita che le lunghezze delle corde hanno fra di loro la proporzione che hanno i quadrati de' numeri delle vibrazioni che si fanno nel medesimo tempo.

Sagr. Adunque, se io ho ben inteso, potrò speditamente sapere la lunghezza d'una corda pendente da qualsivoglia grandissima altezza, quando bene il termine sublime dell'attaccatura mi fusse invisibile e solo si vedesse l'altro estremo basso. Imperò che, se io attaccherò qui da basso un assai grave peso a detta corda e farò che si vada vibrando in qua e in là, e che un amico vadia numerando alcune delle sue vibrazioni e che io nell'istesso tempo vadia parimente contando le vibrazioni che farà un altro mobile appeso a un filo di lunghezza precisamente d'un braccio, da i numeri delle vibrazioni di questi pendoli, fatte nell'istesso tempo, troverò la lunghezza della corda: come, per esempio, ponghiamo che nel tempo che l'amico mio abbia contate venti vibrazioni della corda lunga, io ne abbia contate dugenquaranta del mio filo, che è lungo un braccio; fatti i quadrati delli due numeri venti e dugenquaranta, che sono 400 e 57600, dirò, la lunga corda contener 57600 misure di quelle che il mio filo ne contien 400; e perché il filo è un sol braccio, partirò 57600 per 400, che ne viene 144; e 144 braccia dirò esser lunga quella corda.

Salv. Né vi ingannerete d'un palmo, e massime se piglierete moltitudini grandi di vibrazioni.

Sagr. V. S. mi dà pur frequentemente occasione d'ammirare la ricchezza ed insieme la somma liberalità della natura, mentre da cose tanto comuni, e direi anco in certo modo vili, ne andate traendo notizie molto curiose e nuove, e bene spesso remote da ogni immaginazione. Io ho ben mille volte posto cura alle vibrazioni, in particolare, delle lampade pendenti in alcune chiese da lunghissime corde, inavvertentemente state mosse da alcuno; ma il più che io cavassi da tale osservazione, fu l'improbabilità dell'opinione di quelli che vogliono che simili moti vengano mantenuti e continuati dal mezzo, cioè dall'aria, perché mi parrebbe bene che l'aria avesse un gran giudizio, ed insieme una poca faccenda, a consumar le ore e le ore di tempo in sospignere con tanta regola in qua e in là un peso pendente: ma che io fussi per apprenderne che quel mobile medesimo, appeso a una corda di cento braccia di lunghezza, slontanato dall'imo punto una volta novanta gradi ed un'altra un grado solo o mezzo, tanto tempo spendesse in passar questo minimo, quanto in passar quel massimo arco, certo non credo che mai l'avrei incontrato, ché ancor ancora mi par che tenga dell'impossibile. Ora sto aspettando di sentire che queste medesime semplicissime minuzie mi assegnino ragioni tali di quei problemi musici, che mi possino, almeno in parte, quietar la mente.

Salv. Prima d'ogni altra cosa bisogna avvertire che ciaschedun pendolo ha il tempo delle sue vibrazioni talmente limitato e prefisso, che impossibil cosa è il farlo muover sotto altro periodo che l'unico suo naturale. Prenda pur chi si voglia in mano la corda ond'è attaccato il peso, e tenti quanto gli piace d'accrescergli o scemargli la frequenza delle sue vibrazioni; sarà fatica buttata in vano: ma ben all'incontro ad un pendolo, ancor che grave e posto in quiete, col solo soffiarvi dentro conferiremo noi moto, e moto anche assai grande col reiterare i soffi, ma sotto 'l tempo che è proprio quel delle sue vibrazioni; che se al primo soffio l'aremo rimosso dal perpendicolo mezzo dito, aggiugnendogli il secondo dopo che, sendo ritornato verso noi, comincerebbe la seconda vibrazione, gli conferiremo nuovo moto, e così successivamente con altri soffi, ma dati a tempo, e non quando il pendolo ci vien incontro (che così gl'impediremmo, e non aiuteremmo, il moto); e seguendo, con molti impulsi gli conferiremo impeto tale, che maggior forza assai che quella d'un soffio ci bisognerà a cessarlo.

Sagr. Ho da fanciullo osservato, con questi impulsi dati a tempo un uomo solo far sonare una grossissima campana, e nel volerla poi fermare, attaccarsi alla corda quattro e sei altri e tutti esser levati in alto, né poter tanti insieme arrestar quell'impeto che un solo con regolati tratti gli aveva conferito.

Salv. Esempio che dichiara 'l mio intento non meno acconciamente di quel che questa mia premessa si accomodi a render la ragione del maraviglioso problema della corda della cetera o del cimbalo, che muove e fa realmente sonare quella non solo che all'unisono gli è concorde, ma anco all'ottava e alla quinta. Toccata, la corda comincia e continua le sue vibrazioni per tutto 'l tempo che si sente durar la sua risonanza: queste vibrazioni fanno vibrare e tremare l'aria che gli è appresso, i cui tremori e increspamenti si distendono per grande spazio e vanno a urtare in tutte le corde del medesimo strumento, ed anco di altri vicini: la corda che è tesa all'unisono con la tocca, essendo disposta a far le sue vibrazioni sotto 'l medesimo tempo, comincia al primo impulso a muoversi un poco; e sopraggiugnendogli il secondo, il terzo, il ventesimo e più altri, e tutti ne gli aggiustati e periodici tempi, riceve finalmente il medesimo tremore che la prima tocca, e si vede chiarissimamente andar dilatando le sue vibrazioni giusto allo spazio della sua motrice. Quest'ondeggiamento che si va distendendo per l'aria, muove e fa vibrare non solamente le corde, ma qualsivoglia altro corpo disposto a tremare e vibrarsi sotto quel tempo della tremante corda; sì che se si ficcheranno nelle sponde dello strumento diversi pezzetti di setole o di altre materie flessibili, si vedrà, nel sonare il cimbalo, tremare or questo or quel corpuscolo, secondo che verrà toccata quella corda le cui vibrazioni van sotto 'l medesimo tempo: gli altri non si muoveranno al suono di questa corda, né quello tremerà al suono d'altra corda. Se con l'archetto si toccherà gagliardamente una corda grossa d'una viola, appressandogli un bicchiere di vetro sottile e pulito, quando il tuono della corda sia all'unisono del tuono del bicchiere, questo tremerà e sensatamente risonerà. Il diffondersi poi ampiamente l'increspamento del mezzo intorno al corpo risonante, apertamente si vede nel far sonare il bicchiere, dentro 'l quale sia dell'acqua, fregando il polpastrello del dito sopra l'orlo; imperò che l'acqua contenuta con regolatissimo ordine si vede andar ondeggiando: e meglio ancora si vedrà l'istesso effetto fermando il piede del bicchiere nel fondo di qualche vaso assai largo, nel quale sia dell'acqua sin presso all'orlo del bicchiere; ché parimente, facendolo risonare con la confricazione del dito, si vedranno gl'increspamenti nell'acqua regolatissimi, e con gran velocità spargersi in gran distanza intorno al bicchiere: ed io più volte mi sono incontrato, nel fare al modo detto sonare un bicchiere assai grande e quasi pieno d'acqua, a veder prima le onde nell'acqua con estrema egualità formate, ed accadendo tal volta che 'l tuono del bicchiere salti un'ottava più alto, nell'istesso momento ho visto ciascheduna delle dette onde dividersi in due; accidente che molto chiaramente conclude, la forma dell'ottava esser la dupla.

Sagr. A me ancora è intervenuto l'istesso più d'una volta con mio diletto ed anco utile: imperò che stetti lungo tempo perplesso intorno a queste forme delle consonanze, non mi parendo che la ragione che comunemente se n'adduce da gli autori che sin qui hanno scritto dottamente della musica, fusse concludente a bastanza. Dicono essi, la diapason, cioè l'ottava, esser contenuta dalla dupla, la diapente, che noi diciamo la quinta, dalla sesquialtera, etc.; perché, distesa sopra il monocordo una corda, sonandola tutta e poi sonandone la metà, col mettere un ponticello in mezzo, si sente l'ottava, e se il ponticello si metterà al terzo di tutta la corda, toccando l'intera e poi li due terzi, ci rende la quinta; per lo che l'ottava dicono esser contenuta tra 'l due e l'uno, e la quinta tra il tre e 'l dua. Questa ragione, dico, non mi pareva concludente per poter assegnar iuridicamente la dupla e la sesquialtera per forme naturali della diapason e della diapente: e 'l mio motivo era tale. Tre sono le maniere con le quali noi possiamo inacutire il tuono a una corda: l'una è lo scorciarla; l'altra, il tenderla più, o vogliam dir tirarla; il terzo è l'assottigliarla. Ritenendo la medesima tiratezza e grossezza della corda, se vorremo sentir l'ottava, bisogna scorciarla la metà, cioè toccarla tutta, e poi mezza: ma se, ritenendo la medesima lunghezza e grossezza, vorremo farla montare all'ottava col tirarla più, non basta tirarla il doppio più, ma ci bisogna il quadruplo, sì che se prima era tirata dal peso d'una libbra, converrà attaccarvene quattro per inacutirla all'ottava: e finalmente se, stante la medesima lunghezza e tiratezza, vorremo una corda che, per esser più sottile, renda l'ottava, sarà necessario che ritenga solo la quarta parte della grossezza dell'altra più grave. E questo che dico dell'ottava, cioè che la sua forma presa dalla tensione o dalla grossezza della corda è in duplicata proporzione di quella che si ha dalla lunghezza, intendasi di tutti gli altri intervalli musici: imperò che quello che ci dà la lunghezza con la proporzion sesquialtera, cioè col sonarla tutta e poi li due terzi, volendolo cavar dalla tiratezza o dalla sottigliezza, bisogna duplicar la proporzione sesquialtera, pigliando la dupla sesquiquarta, e se la corda grave era tesa da quattro libbre di peso, attaccarne all'acuta non sei, ma nove, e quanto alla grossezza, far la corda grave più grossa dell'acuta secondo la proporzione di nove a quattro, per aver la quinta. Stante queste verissime esperienze, non mi pareva scorger ragione alcuna per la quale avesser i sagaci filosofi a stabilir, la forma dell'ottava esser più la dupla che la quadrupla, e della quinta più la sesquialtera che la dupla sesquiquarta. Ma perché il numerar le vibrazioni d'una corda, che nel render la voce le fa frequentissime, è del tutto impossibile, sarei restato sempre ambiguo se vero fusse che la corda dell'ottava, più acuta, facesse nel medesimo tempo doppio numero di vibrazioni di quelle della più grave, se le onde permanenti per quanto tempo ci piace, nel far sonare e vibrare il bicchiere, non m'avessero sensatamente mostrato come nell'istesso momento che alcuna volta si sente il tuono saltare all'ottava, si veggono nascere altre onde più minute, le quali con infinita pulitezza tagliano in mezzo ciascuna di quelle prime.

Salv. Bellissima osservazione per poter distinguer ad una ad una le onde nate dal tremore del corpo che risuona, che son poi quelle che, diffuse per l'aria, vanno a far la titillazione su 'l timpano del nostro orecchio, la quale nell'anima ci doventa suono. Ma dove che il vederle ed osservarle nell'acqua non dura se non quanto si continua la confricazion del dito, ed anco in questo tempo non sono permanenti, ma continuamente si fanno e si dissolvono, non sarebbe bella cosa quando se ne potesse far con grand'esquisitezza di quelle che restassero lungo tempo, dico mesi ed anni, sì che desser commodità di poterle misurare ed agiatamente numerare?

Sagr. Veramente io stimerei sommamente una tale invenzione.

Salv. L'invenzione fu del caso, e mia fu solamente l'osservazione e 'l far di essa capitale e stima come di riprova di nobil contemplazione, ancor che fattura in se stessa assai vile. Raschiando con uno scarpello di ferro tagliente una piastra d'ottone per levarle alcune macchie, nel muovervi sopra lo scarpello con velocità, sentii una volta e due, tra molte strisciate, fischiare e uscirne un sibilo molto gagliardo e chiaro; e guardando sopra la piastra, veddi un lungo ordine di virgolette sottili, tra di loro parallele e per egualissimi intervalli l'una dall'altra distanti. Tornando a raschiar di nuovo più e più volte, m'accorsi che solamente nelle raschiate che fischiavano lasciava lo scarpello le 'ntaccature sopra la piastra; ma quando la strisciata passava senza sibilo, non restava pur minima ombra di tali virgolette. Replicando poi altre volte lo scherzo, strisciando ora con maggiore ed ora con minor velocità, il sibilo riusciva di tuono or più acuto ed or più grave; ed osservai, i segni fatti nel suono più acuto esser più spessi, e quelli del più grave più radi, e tal volta ancora, secondo che la strisciata medesima era fatta verso 'l fine con maggior velocità che nel principio, si sentiva il suono andarsi inacutendo, e le virgolette si vedeva esser andate inspessendosi, ma sempre con estrema lindura e con assoluta equidistanza segnate; ed oltre a ciò, nelle strisciate sibilanti sentivo tremarmi il ferro in pugno, e per la mano scorrermi certo rigore: ed in somma si vede e sente fare al ferro quello per appunto che facciamo noi nel parlar sotto voce e nell'intonar poi il suono gagliardo, che, mandando fuora il fiato senza formare il suono, non sentiamo nella gola e nella bocca farsi movimento alcuno, rispetto però ed in comparazione del tremor grande che sentiamo farsi nella laringe ed in tutte le fauci nel mandar fuora la voce, e massime in tuono grave e gagliardo. Ho anco tal volta tra le corde del cimbalo notatone due unisone alli due sibili fatti strisciando al modo detto, e de i più differenti di tuono, de i quali due precisamente distavano per una quinta perfetta; e misurando poi gl'intervalli delle virgolette dell'una e dell'altra strisciata, si vedeva, la distanza che conteneva quarantacinque spazii dell'una, contenere trenta dell'altra, quale veramente è la forma che si attribuisce alla diapente. Ma qui, prima che passare più avanti, voglio avvertirvi, che delle tre maniere d'inacutire il suono, quella che voi referite alla sottigliezza della corda, con più verità deve attribuirsi al peso. Imperò che l'alterazione presa dalla grossezza risponde quando le corde siano della medesima materia: e così una minugia per far l'ottava deve esser più grossa quattro volte dell'altra pur di minugia; ed una d'ottone, più grossa quattro volte d'un'altra d'ottone: ma s'io vorrò far l'ottava con una d'ottone ad una di minugia, non si ha da ingrossar quattro volte, ma sì ben farla quattro volte più grave; sì che, quanto alla grossezza, questa di metallo non sarà altrimenti quattro volte più grossa, ma ben quadrupla in gravità, che tal volta sarà più sottile che la sua rispondente all'ottava, più acuta, che sia di minugia: onde accade che incordandosi un cimbalo di corde d'oro ed un altro d'ottone, se saranno della medesima lunghezza, grossezza e tensione, per esser l'oro quasi il doppio più grave, riuscirà l'accordatura circa una quinta più grave. E qui notisi come alla velocità del moto più resiste la gravità del mobile che la grossezza, contro a quello che a prima fronte altri giudicherebbe; che ben pare che, ragionevolmente, più dovesse esser ritardata la velocità dalla resistenza del mezzo all'esser aperto in un mobile grosso e leggiero, che in uno grave e sottile; tuttavia in questo caso accade tutto l'opposito. Ma seguitando il primo proposito, dico che non è la ragion prossima ed immediata delle forme de gl'intervalli musici la lunghezza delle corde, non la tensione, non la grossezza, ma sì bene la proporzione de i numeri delle vibrazioni e percosse dell'onde dell'aria che vanno a ferire il timpano del nostro orecchio, il quale esso ancora sotto le medesime misure di tempi vien fatto tremare. Fermato questo punto, potremo per avventura assegnar assai congrua ragione onde avvenga che di essi suoni, differenti di tuono, alcune coppie siano con gran diletto ricevute dal nostro sensorio, altre con minore, ed altre ci feriscano con grandissima molestia; che è il recar la ragione delle consonanze più o men perfette e delle dissonanze. La molestia di queste nascerà, credo io, dalle discordi pulsazioni di due diversi tuoni che sproporzionatamente colpeggiano sopra 'l nostro timpano, e crudissime saranno le dissonanze quando i tempi delle vibrazioni fussero incommensurabili; per una delle quali sarà quella quando di due corde unisone se ne suoni una con tal parte dell'altra quale è il lato del quadrato del suo diametro: dissonanza simile al tritono o semidiapente. Consonanti, e con diletto ricevute, saranno quelle coppie di suoni che verranno a percuotere con qualche ordine sopra 'l timpano; il qual ordine ricerca, prima, che le percosse fatte dentro all'istesso tempo siano commensurabili di numero, acciò che la cartilagine del timpano non abbia a star in un perpetuo tormento d'inflettersi in due diverse maniere per acconsentire ed ubbidire alle sempre discordi battiture: sarà dunque la prima e più grata consonanza l'ottava, essendo che per ogni percossa che dia la corda grave su 'l timpano, l'acuta ne dà due, tal che amendue vanno a ferire unitamente in una sì, e nell'altra no, delle vibrazioni della corda acuta, sì che di tutto 'l numero delle percosse la metà s'accordano a battere unitamente; ma i colpi delle corde unisone giungon sempre tutti insieme, e però son come d'una corda sola, né fanno consonanza. La quinta diletta ancora, atteso che per ogni due pulsazioni della corda grave l'acuta ne dà tre, dal che ne séguita che, numerando le vibrazioni della corda acuta, la terza parte di tutte s'accordano a battere insieme, cioè due solitarie s'interpongono tra ogni coppia delle concordi; e nella diatesseron se n'interpongon tre. Nella seconda, cioè nel tuono sesquiottavo, per ogni nove pulsazioni una sola arriva concordemente a percuotere con l'altra della corda più grave; tutte l'altre sono discordi e con molestia ricevute su 'l timpano, e giudicate dissonanti dall'udito.

Simp. Vorrei con maggior chiarezza spiegato questo discorso.

Salv. Sia questa linea AB lo spazio e la dilatazione d'una vibrazione della corda grave, e la linea CD quella della corda acuta, la quale con l'altra renda l'ottava, e dividasi la AB in mezzo in E: è manifesto, che cominciando a muoversi le corde nei termini A, C, quando la vibrazione acuta sarà pervenuta al termine D, l'altra si sarà distesa solamente sino al mezzo E, il quale, non sendo termine del moto, non percuote, ma ben si fa colpo in D. Ritornando poi la vibrazione dal D in C, l'altra passa da E in B, onde le due percosse di B e di C battono unitamente su 'l timpano: e tornando a reiterarsi le simili seguenti vibrazioni, si concluderà, alternatamente in una sì e nell'altra no delle vibrazioni C, D accadere l'unione delle percosse con quelle di A, B. Ma le pulsazioni de i termini hanno sempre per compagne una delle C, D, e sempre la medesima: il che è manifesto; perché, posto che A, C battano insieme, nel passar A in B, C va in D e torna in C, tal che C batte con B; e nel tempo che B torna in A, C passa per D e torna in C, sì che i colpi A, C si fanno insieme. Ma sieno ora le due vibrazioni AB, CD quelle che producono la diapente, i tempi delle quali sono in proporzion sesquialtera, e dividasi la AB della corda grave in tre parti eguali in E, O, e intendansi le vibrazioni cominciare nell'istesso momento da i termini A, C: è manifesto che nella percossa che si farà nel termine D, la vibrazione di AB sarà giunta solamente in O; il timpano dunque riceve la percossa D sola: nel ritorno poi da D in C, l'altra vibrazione passa da O in B e ritorna in O, facendo la pulsazione in B, che pure è sola e di contrattempo (accidente da considerarsi); perché, avendo poi posto le prime pulsazioni fatte nell'istesso momento nei termini A, C, la seconda, che fu sola del termine D, si fece dopo quanto importa il tempo del transito CD, cioè AO, ma la seguente, che si fa in B, dista dall'altra solo quanto è il tempo di OB, che è la metà: continuando poi il ritorno da O in A, mentre da C si va in D, si viene a far le due pulsazioni unitamente in A e D. Seguono poi altri periodi simili a questi, cioè con l'interposizione di due pulsazioni della corda acuta, scompagnate e solitarie, e una della corda grave, pur solitaria e interposta tra le due solitarie dell'acuta. Sì che, se noi figureremo il tempo diviso in momenti, cioè in minime particole eguali; posto che nei due primi dalle concordi pulsazioni fatte in A, C si passi in O, D, e in D si batta; che nel terzo e quarto momento si torni da D in C, battendo in C, e che da O si passi per B e si torni in O, battendosi in B; e che finalmente nel quinto e sesto momento da O e C si passi in A e D, battendo in amendue; avremo sopra 'l timpano le pulsazioni distribuite con tal ordine, che poste le pulsazioni delle due corde nel medesimo instante, due momenti dopo riceverà una percossa solitaria, nel terzo momento un'altra pur solitaria, nel quarto un'altra sola, e due momenti dopo, cioè nel sesto, due congiunte insieme: e qui finisce il periodo, e, per dir così, l'anomalia, il qual periodo si va poi più volte replicando.

Sagr. Io non posso più tacere: è forza ch'io esclami il gusto che sento nel vedermi tanto adequatamente rese ragioni di effetti che tanto tempo m'hanno tenuto in tenebre e cecità. Ora intendo perché l'unisono non differisce punto da una voce sola: intendo perché l'ottava è la principal consonanza, ma tanto simile all'unisono, che come unisono si prende e si accompagna con le altre; simile è all'unisono, perché, dove le pulsazioni delle corde unisone vanno a ferire tutte insieme sempre, queste della corda grave dell'ottava vanno tutte accompagnate da quelle dell'acuta, e di queste una s'interpone solitaria ed in distanze eguali ed in certo modo senza fare scherzo alcuno, onde tal consonanza ne diviene sdolcinata troppo e senza brio. Ma la quinta, con quei suoi contrattempi, e con l'interpor tra le coppie delle due pulsazioni congiunte due solitarie della corda acuta ed una pur solitaria della grave, e queste tre con tanto intervallo di tempo quanto è la metà di quello che è tra ciascuna coppia e le solitarie dell'acuta, fa una titillazione ed un solletico tale sopra la cartilagine del timpano, che temperando la dolcezza con uno spruzzo d'acrimonia, par che insieme soavemente baci e morda.

Salv. È forza, poiché veggo che V. S. gusta tanto di queste novellizie, che io gli mostri il modo col quale l'occhio ancora, non pur l'udito, possa recrearsi nel veder i medesimi scherzi che sente l'udito. Sospendete palle di piombo, o altri simili gravi, da tre fili di lunghezze diverse, ma tali che nel tempo che il più lungo fa due vibrazioni, il più corto ne faccia quattro e 'l mezzano tre, il che accaderà quando il più lungo contenga sedici palmi o altre misure, delle quali il mezzano ne contenga nove ed il minore quattro; e rimossi tutti insieme dal perpendicolo e poi lasciatigli andare, si vedrà un intrecciamento vago di essi fili, con incontri varii, ma tali che ad ogni quarta vibrazione del più lungo tutti tre arriveranno al medesimo termine unitamente, e da quello poi si partiranno, reiterando di nuovo l'istesso periodo: la qual mistione di vibrazioni è quella che, fatta dalle corde, rende all'udito l'ottava con la quinta in mezzo. E se con simile disposizione si andranno temperando le lunghezze di altri fili, sì che le vibrazioni loro rispondano a quelle di altri intervalli musici, ma consonanti, si vedranno altri ed altri intrecciamenti, e sempre tali, che in determinati tempi e dopo determinati numeri di vibrazioni tutti i fili (siano tre o siano quattro) si accordano a giugner nell'istesso momento al termine di loro vibrazioni, e di lì a cominciare un altro simil periodo. Ma quando le vibrazioni di due o più fili siano o incommensurabili, sì che mai non ritornino a terminar concordemente determinati numeri di vibrazioni, o se pur, non essendo incommensurabili, vi ritornano dopo lungo tempo e dopo gran numero di vibrazioni, allora la vista si confonde nell'ordine disordinato di sregolata intrecciatura, e l'udito con noia riceve gli appulsi intemperati de i tremori dell'aria, che senza ordine o regola vanno a ferire su 'l timpano.

Ma dove, Signori miei, ci siamo lasciati trasportare per tante ore da i vani problemi ed inopinati discorsi? Siamo giunti a sera, e della proposta materia abbiamo trattato pochissimo o niente; anzi ce ne siamo in modo disviati, che a pena mi sovviene della prima introduzzione e di quel poco ingresso che facemmo come ipotesi e principio delle future dimostrazioni.

Sagr. Sarà dunque bene che ponghiamo per oggi fine a i nostri ragionamenti, dando commodo alla mente di andarsi nel riposo della notte tranquillando, per tornar poi domani (quando piaccia a V. S. di favorirci) a i discorsi desiderati e principalmente intesi.

Salv. Non mancherò d'esser qua all'istessa ora di oggi a servirle e goderle.

Finisce la prima Giornata