"How large should be a propeller to develop the same traction of a couple of smaller propellers, geometrically similar to it, rotating at the same angular velocity, and working in kinematic similitude condition (obviously)?"
The first thing that comes to mind is to try with a double radius (see picture below):
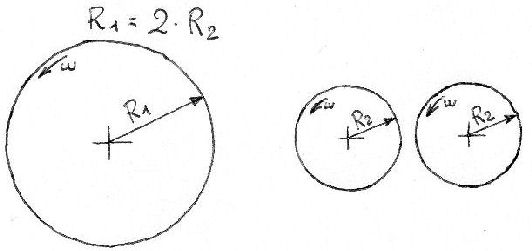
In this case we shall have:
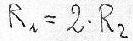
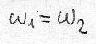
In order to be in kinematic similitude conditions, it is necessary that:
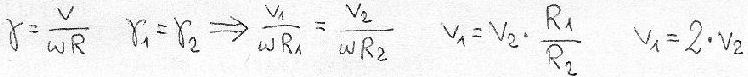
So, in order to have the same aerodynamic coefficients of the two smaller propellers, the large propeller must advance at double speed (that is, the aircraft must fly at double speed).
Now, having examined the conditions to comply with in order to have kinematic similitude, we can calculate the ratio of the traction developed by the large prop to the traction developed by one small prop.
By applying Rénard's 1st law, we obtain:
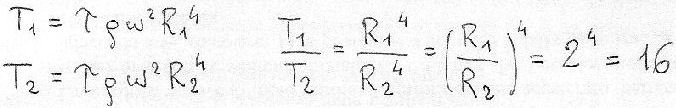
So, a double radius propeller, under the described hypotheses, develops a traction 8 times greater than the couple of smaller propellers.
Then let's try a propeller having its disk surface double in respect with one small propeller (since equivalent at the pair of small props):

In this case we obtain, making the calculations (I enjoy to let the reader evaluate how fast must fly the large propeller to verify kinematic similitude):
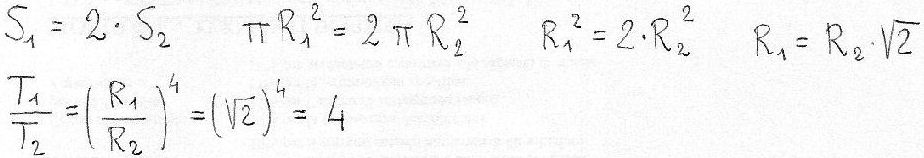
Summing up conclusions, the propeller with double-area disk must have a radius increased by a factor "square root of 2" (that is approximately 1.4142), and the large propeller, alone, develops a traction double of the couple of small propellers.
The correct procedure for finding immediately the solution to the initial question is the following (also in this case I enjoy to let the reader compute the speed by himself):

So the propeller we were looking for must have a radius of approximately 1.1892 times the small propellers (see picture below):

This is a free site, that makes itself know mostly thanks to the echoing of its users; also you can contribute: signal this site to your interested friends. Thank you very much indeed.