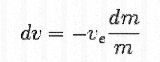 | 1) |
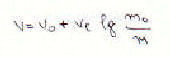 | 2) |
For Newton's 2nd law, the force acting on the rocket (that is: thrust) equals its mass multiplied by acceleration:
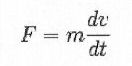 | 3) |
For Newton's 3rd law (action-reaction principle) F is also the force which increased the momentum of exhausted gas; this force equals the derivative in respect of time of the momentum of exhausted gas; in an infinitesimal time interval dt, a mass -dm with speed ve adds to the already ejected gas, so the momentum increase is -ve·dm; thrust is therefore:
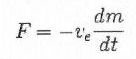 | 4) |
By putting equal the 3) and 4):
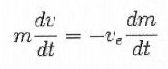 | 5) |
The rigorous demonstration involves use of all the terms present in the problem, considered as an isolated system made of rocket+ejected gas, observed from an inertial reference axis tern.
The thrust force, which rocket and ejected gas exchange each other, is an internal force and doesn't modify the total momentum of the system; so Newton's 2nd law in its general form is applied:
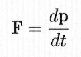 | 6) |
considering the whole expression of the derivative:
 | 7) |
Since F = 0, indicating by capital letters the quantities relevant to rocket and by small letters those relevant to gas, the 7) may be written
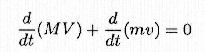 | 8) |
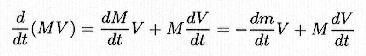 | 9) |
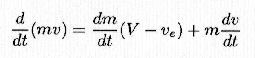 |
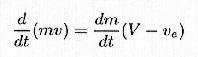 | 10) |
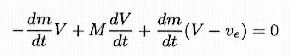 |
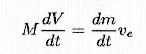 | 11) |
In order to obtain rocket velocity it's sufficient to bear in mind that, in the 11), the ejected gas quantity is equal to the rocket mass decrease, dm = -dM, and so
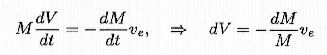 |
The 2) can be re-written therefore:
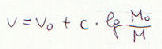 | 12) |
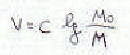 | 13) |
 | 14) |
 | 15) |
 | 16) |
 | 17) |
 |
 |
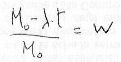 |
 |
 |
 |
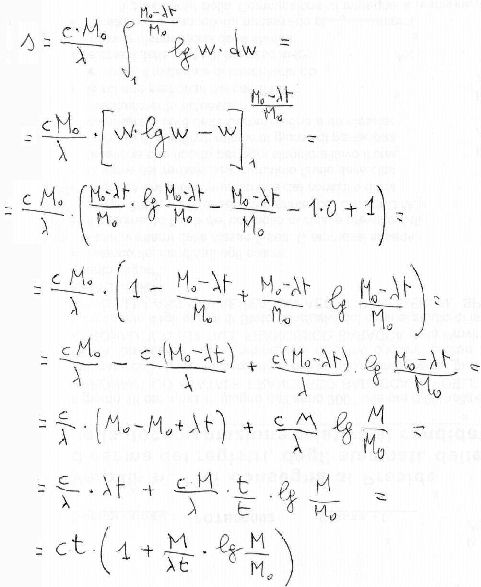 |
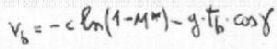 | formula 2) quoted at p.7-4, with corrections | |
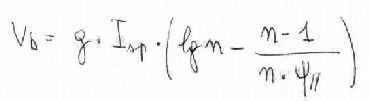 | formula 8) quoted at p.8-1, with corrections |
The meaning of symbols that appear in this two formulas is as follows:
ln = lg = natural logarithm (base e);
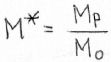
| MP = | propellant mass; |
| tb = | combustion time; |
| γ = | launch angle from vertical; |
| Isp = | specific impulse; |
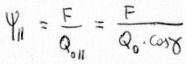
| F = | thrust; |
| Q0 = | initial weight of the rocket; |
| n = | mass ratio = M0/Mf = M0/(M0 - MP); |
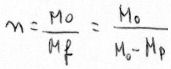
| Mf = | rocket mass at combustion end. |
We get, through simple passages:
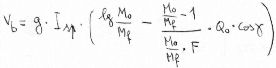 | 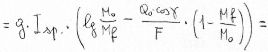 |
 | 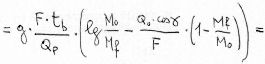 |
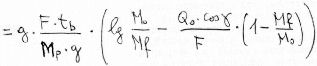 | 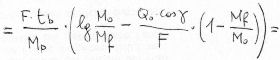 |
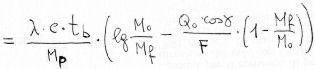 | 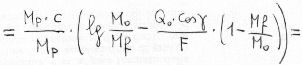 |
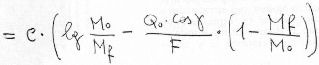 | 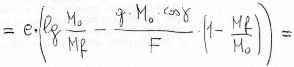 |
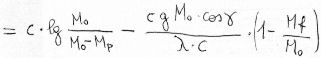 |  |
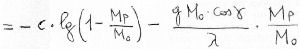 | 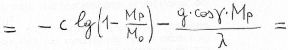 |
 | 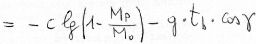 |
So, the formula 8), which uses the specific impulse, has a general validity, while the 2), which uses the gas ejection speed c, is valid for adapted nozzle only.
