Nel 1854, il matematico britannico George Boole (1815 - 1864), elaborò una matematica algebrica - di fondamentale importanza nella progettazione degli odierni computer - che da lui prese il nome. Nell'algebra booleana le procedure di calcolo si possono effettuare grazie a operatori matematici (AND, OR, NOT, ecc.) corrispondenti alle leggi della logica.
L'algebra di Boole entrò prepotentemente alla ribalta nel 1936, quando il matematico britannico Alan Mathison Turing (1912-1954), immaginò una "macchina" o "automa" (che oggi sembra banale), esistente unicamente a livello teorico, con la quale dimostrò formalmente la possibilità di realizzare una macchina in grado di eseguire qualsiasi algoritmo: una procedura di calcolo o, più in generale, l'elenco delle operazioni necessarie per risolvere un problema in un numero finito di operazioni.
Turing in tal modo aprì la strada al campo di quelle ricerche infornatiche che prendono il nome di intelligenza artificiale. Inoltre, nello scritto Macchine calcolatrici e intelligenza (1950), propose un metodo denominato "test di Turing" per determinare se le macchine possano essere in grado di pensare.
Per Alan Turing, la prima questione da risolvere consisteva nel precisare le azione elementari che compiamo quando eseguiamo un calcolo. In effetti, una semplice operazione di somma viene appresa facilmente fin dalle scuole elementari; è un'operazione che effettuiamo meccanicamente ogni giorno, quando per esempio acquistiamo due oggetti dallo stesso fornitore, o quando conttabilizziamo il denaro che abbiamo in tasca. L'addizione è dunque un'operazione banale, ma sappiamo definirne l'algoritmo?
|
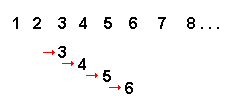
Per far questo, supponiamo di eseguire una somma di due numeri (naturali), per fissare le idee, 2+4.

Per ottenere il risultato della somma proposta, dobbiamo seguire questi passaggi:
Questo è dunque l'algoritmo della somma di due numeri.
La sequenza di operazioni esaminata, si presta anche per eseguire moltiplicazioni. Per esempio, 2 x 3; in quanto si tratta di addizionare 3 volte il numero 2: 2 + 2 + 2
Per ottenere il risultato della moltiplicazione proposta, dobbiamo seguire questi passaggi:
Come si vede, si è aggiunto un secondo controllo. Con analogo procedimento, è possibile anche l'elevazione a potenza. Per esempio, 23 = 2 x 2 ripetuta 3 volte. In questo caso, si dovrà aggiungere un terzo contatore.
Si potrebbe vedere facilmente (ma la questione è irrilevante per questa discussione) che il procedimento utilizzato per addizioni, moltiplicazioni ed elevazione a potenza, vale anche per le operazioni inverse: sottrazione, divisione (una successione di sottrazioni: 17/5 = 17 - 5 - 5 - 5 = 3 con il riporto di 2), estrazione di radice.
Dimostrata l'esistenza di algoritmi per effettuare le operazione matematiche fondamentali, la seconda questione da risolvere consisteva nel precisare l'occorrente per sviluppare la sequenza di operazioni previste... naturalmente non ci riferiamo a carta e penna, ma a qualcosa di più complesso. Non molto, però.
Come primo passo, occorre definire i simboli con i quali rappresentiamo i numeri su cui operiamo, le operazioni da effettuare e la sequenza di operazioni impostate.
La scrittura dei numeri è molto semplice, rappresenteremo lo zero con I, il numero uno con II, il numero due con III, il numero tre con IIII, e così via. Con questo simbolismo, per passare da un numero al successivo, si aggiunge una barretta; per passare al precedente, si elimina una barretta.
Ovviamente, occorre anche un supporto sul quale riportare i simboli: adotteremo un nastro di carta supposto di lunghezza adeguata per contenere qualsiasi algoritmo.
Il nastro è diviso in celle, ognuna delle quali contiene un solo simbolo: per scrivere il numero 3, occorreranno quindi tre celle.
Ovviamente, il nastro deve essere collegato ad un meccanismo che gli permetta di scorrere per esaminare il contenuto di ogni cella, e per portarsi in una zona di celle nella quale annoteremo i risultati parziali ottenuti, o altri simboli eventualmente necessari: quelli per eseguire operazioni di somma o sottrazione e per contare le ripetizioni.
La "macchina di Turing" può operare sulla striscia in diversi modi:
La macchina, a seconda dello stato in cui si trova e del simbolo che legge sul nastro, esegue una delle azioni possibili e passa ad un nuovo stato o rimane nel suo stato iniziale. L'automa si ferma quando, in corrispondenza dello stato in cui si trova e del carattere che legge, non trova ulteriori istruzioni.
Con la macchina di Turing (che, per quanto possa sembrare strano, riassume la struttura funzionale di un computer) è possibile risolvere anche problemi non numerici; infatti basta associare ad i simboli un significato alfabetico o alfanumerico.
Turing era convinto che la sua macchina potesse effettuare qualsiasi operazione logica e, programmata con la necessaria abilità entro il duemila avrebbe potuto simulare l'intelligenza umana. Addirittura propose come si sarebbe svolto il test di controllo.
 Una persona si trova davanti ad un terminale e con la tastiera scrive delle domande e riceve delle risposte.
Una persona si trova davanti ad un terminale e con la tastiera scrive delle domande e riceve delle risposte.  D'all'altro capo del terminale ci sono una macchiana ed un operatore umano che forniscono alternativamente le risposte alle domando. Se la persona non è in grado di distinguere quando sta interloquendo con una macchina e quando con un operatore umano, allora la macchina è intelligente.
D'all'altro capo del terminale ci sono una macchiana ed un operatore umano che forniscono alternativamente le risposte alle domando. Se la persona non è in grado di distinguere quando sta interloquendo con una macchina e quando con un operatore umano, allora la macchina è intelligente.
Finora nessun programma ha superato il test di Turing. Il più noto è Eliza, un programma scritto nel 1966 da Joseph Weizenbaum. Eliza è una psicoterapeuta che simula una conversazione tra lei (il medico), e voi (il paziente). Il programma non era molto convincente; tuttavia, ai primordi dei computer domestici molte persone erano convinte che un computer fosse un "cervello" elettronico e quindi non facevano molto caso alla piega bizzara che ben presto delineava la "seduta". D'altra parte, il test di Turing non prevedeva l'ingenuità della persona incaricata di saggiare la macchina: doveva essere un operatore esperto.
Dopo Eliza sono stati realizzati molti programmi per simulare l'intelligenza; sebbene alcuni siano progettati per argomenti ben definiti (per es. teatro di Shakespear), nessuno è stato in grado di ingannare un giudice esperto.
Se volete saperne di più, potete trovare alcuni programmi su questo sito http://www.toptown.com/hp/sjlaven