Trasformazioni di Lorentz

Derivazione matematica

La velocità della luce è la stessa in tutti i sistemi di riferimento in moto uniforme rispetto alla sorgente: tutte le enormi conseguenze della teoria della relatività ristretta seguono da questa semplice ipotesi. Si deve quindi determinare una trasformazione delle coordinate spazio-temporali per la quale la velocità della luce risulti indipendente dal moto della sorgente o del ricevitore.

Sia S il sistema di riferimento in cui la sorgente è ferma: posizioni e tempi, misurati da un osservatore in questo sistema, verranno indicati con i simboli non accentati x, y, z, t. Se una sorgente di luce è posta nell'origine del sistema S, l'equazione del fronte d'onda sferico, emesso al tempo t = 0, è

(1)

Tale equazione descrive una superficie sferica il cui raggio cresce con velocità c.

Sia S' il sistema di riferimento in moto: le posizioni e i tempi misurati da un osservatore in questo sistema verranno indicati con i simboli x', y', z', t'. Supponiamo, per convenienza, che lo zero di t' coincida con lo zero di t e che l'origine di x', y', z', coincida con la posizione occupata dalla sorgente di luce, in S, a questo istante zero. Allora, per un osservatore in S' l'equazione del fronte d'onda sferico deve essere:

(2)

Supponiamo che il sistema S' si muova in direzione +x , con velocità costante v rispetto ad S. Le trasformazioni di Galileo collegano le misure effettuate nei due sistemi mediante le equazioni:

(3)

Sostituendo le (3) nella (2), si ottiene:

che non è certamente in accordo con la (1): quindi le trasformazioni galileiane falliscono. Se è valido il principio di costanza della velocità della luce, deve esistere una trasformazione che si riduce a quella di Galileo per v/c tendente a zero e che trasforma la (2) nella (1). Immaginiamo che la nuova trasformazione sia semplice per y' e z', poiché i termini y'² e z'² , che compaiono nella (2), si trasformano esattamente in y ² e z ² nella (1). Occorre una trasformazione che sia lineare in x e t, poiché vogliamo ottenere una sfera che si espanda con velocità uniforme. Inoltre non si può lasciare inalterata la trasformazione t' = t, se vogliamo cancellare i termini indesiderabili -2xvt+v ²t², perchè qualcosa si deve certamente aggiungere per cancellare questi termini. Proviamo con una trasformazione del tipo

,

dove f è una costante da determinarsi. Allora la (2) diviene

(4)

I termini in xt si elidono se si pone

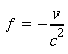e quindi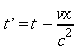

Con questo valore di f la (4) si può scrivere

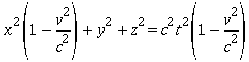
Questa è più vicina alla (1), ma resta ancora un fattore di scala indesiderato, (1-v²/c²) , che moltiplica x² e t². Questo fattore si può eliminare prendendo come trasformazione la seguente:

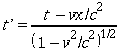
Queste sono le cosiddette trasformazioni di Lorentz (queste trasformazioni hanno una lunga storia: vennero usate per la prima volta da J.Larmor per spiegare il risultato negativo dell'eperienza di Michelson-Morley nel suo Aether and Matter (1900)).

(La Fisica di Berkeley 1, Meccanica, ed.Zanichelli)

indice