Elettrotecnica

Correnti continue

Elettrostatica

Magnetismo

Transitori

Correnti alternate

Sistemi trifase

Semplici esercizi propedeutici allo svolgimento di quelli più complessi

Esercizio n. 1

Attraverso la sezione di un conduttore metallico passa in ogni minuto la quantità di carica Q = 0,36 C.

Calcolare l’intensità di corrente che attraversa il conduttore.

R: 6 mA ;

Esercizio n. 2

Calcolare la carica totale che attraversa la sezione di un conduttore metallico in cui circola una corrente di intensità I = 0,04 A per un tempo di 5 s:

R: 0,2 C ;

Esercizio n. 3

Ai capi di un conduttore è applicata la d.d.p. di 18 V.

Calcolare la sua resistenza, sapendo che esso è attraversato da una corrente di intensità 27∙10^-3 A:

R: 2/3 kΩ ;

Esercizio n. 4

Quale d.d.p. si deve applicare agli estremi di un conduttore metallico avente resistenza R=12 Ω, se si vuole che esso sia percorso da una corrente di intensità I = 20 A:

R: 240 V ;

Esercizio n. 5

Determinare l’intensità di corrente che percorre un conduttore di resistenza R = 200 kΩ, quando si applica ai suoi estremi una d.d.p. di 500 V:

R: 2,5 mA ;

Esercizio n. 6

Un alimentatore stabilizzato mantiene una d.d.p. fissa ai propri morsetti. Quando lo si collega ad un resistore da 150 Ω esso eroga una corrente di 80 mA. Quale corrente attraverserà un resistore da 600 Ω, connesso ai morsetti del medesimo generatore?

R: 20 mA ;

Esercizio n. 7

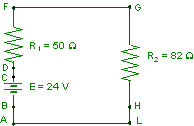
Si consideri il circuito di figura.
a) Si calcoli l’intensità della corrente circolante.
b) Supponendo che il potenziale nel punto A sia nullo V_A=0, specificare i valori del potenziale elettrico nei punti B, C, D, F, G, H, L.

R: 2/11 A ; 0 V ; 24 V ; 24 V ; 164/11 V ; 164/11 V ; 0 V ; 0V ;

Esercizio n. 8

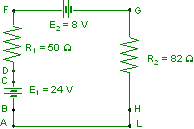
Si consideri il circuito di figura.
a) Si calcoli l’intensità della corrente circolante.
b) Supponendo che il potenziale nel punto A sia nullo V_A=0, specificare i valori del potenziale elettrico nei punti B, C, D, F, G, H, L.
:

R: 4/33 A ; 0 V ; 24 V ; 24 V ; 592/33 V ; 328/33 V ; 0 V ; 0V ;

Esercizio n. 9

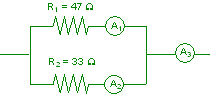
Nella figura che segue è rappresentata una parte di un circuito elettrico. La resistenza interna degli amperometri può essere considerata nulla. Se l’amperometro A₁ indica una corrente I₁ = 200 mA, quanto segnano gli altri due amperometri?

R: 0,28 A ; 0,48 A ;

Esercizio n. 10

Tre resistori sono posti in serie. Il primo ha il valore di 10 Ω, mentre gli altri hanno ciascuno valore doppio del precedente.

Calcolare la resistenza complessiva del sistema.

Calcolare, inoltre, quale valore avrebbe la resistenza complessiva se i resistori fossero inseriti in parallelo.

R: 70 Ω ; 40/7 Ω ;

Esercizio n. 11

Calcolare il valore della resistenza da inserire in parallelo ad un’altra resistenza da 100 Ω per ottenere una resistenza complessiva di 20 Ω.

R: 25 Ω ;

Esercizio n. 12

Determinare il rapporto tra le d.d.p. esistenti ai capi di due resistenze del valore rispettivamente di 500 Ω e di 800 Ω, connesse in serie ad un generatore di tensione.

R: 5/8 ;

Esercizio n. 13

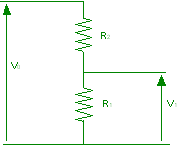
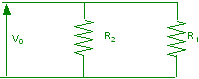
Ai capi di una serie di due resistenze R1 ed R2 viene stabilita una d.d.p. V₀ come nella figura. Determinare la d.d.p. V₁ ai capi di R₁.

R: V₀∙[R₁/(R₁+R₂)] ;

Esercizio n. 14

Determinare il rapporto tra le correnti che passano nelle due resistenze R₁ ed R₂ collegate in parallelo ad un generatore di tensione.

R: R₂/R₁ ;

Esercizio n. 15

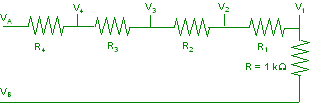
Nel circuito di figura sia V_A = 10 V e V_B = 0 V.

Determinare i valori delle resistenze R₁, R₂, R₃ ed R₄ in modo che si abbia V₁ = 2 V, V₂ = 4 V, V₃ = 6 V, V₄ = 8 V.

R: 1000 Ω ; 1000 Ω ; 1000 Ω ; 1000 Ω ;

Esercizio n. 16

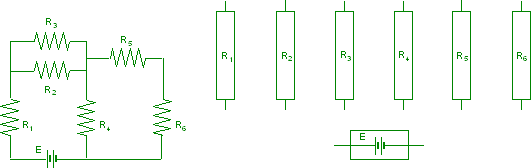
Nella prima figura è mostrato lo schema elettrico di un circuito.
Nella seconda sono rappresentati i componenti reali.

Disegnare i collegamenti fra i componenti reali necessari a realizzare lo schema elettrico proposto.
 

Esercizio n. 17

Un conduttore, ai cui estremi è applicata una d.d.p. di 120 V, è attraversato da una corrente di intensità I = 10 mA.
a) Calcolare la potenza erogata dal generatore

b) Se il collegamento è mantenuto per 30 minuti calcolare l’energia fornita dal generatore.
 

R: 1,2 W ; 2160 J ;

Esercizio n. 18

Calcolare l’energia trasferita ad un utilizzatore ai capi del quale è mantenuta una d.d.p. di 20 V quando è attraversato da una carica di 3,0 C.

R: 60 J ;

Esercizio n. 19

Una lampadina assorbe una potenza pari a 48 W quando ai suoi capi vi è una d.d.p. di 110 V.

Calcolare l’intensità di corrente che attraversa la lampadina e la sua resistenza nelle condizioni indicate.

R: 0,44 A ; 250 Ω ;

Esercizio n. 20

Calcolare la potenza assorbita da una lampadina che presenta una resistenza di 440 Ω quando ai suoi capi è mantenuta una d.d.p. di 220 V.

R: 110 W ;

Esercizio n. 21

La potenza elettrica fornita ad una certa abitazione dall’ENEL è 3000 W, con la d.d.p. di 220 V.

Calcolare la massima intensità di corrente che può circolare nell’impianto.

R: 13,64 A ;

Esercizio n. 22

La batteria di un’automobile ha f.e.m. pari a 12 V ed una resistenza interna r = 0,050 Ω.

Quando si aziona il motorino di avviamento vengono assorbiti 40 A di corrente.

Qual è la d.d.p. ai capi della batteria durante il funzionamento del motorino?

R: 10 V ;

Esercizio n. 23

Se ad una pila si collega una resistenza R = 50 Ω, questa è percorsa da una corrente di 0,80 A.

Collegando in parallelo alla resistenza R una seconda resistenza R₁ = 25 Ω la corrente complessiva diventa 2,0 A.

Calcolare la resistenza interna e la f.e.m. della pila.

R: 44,44 V ; 5,55 Ω ;

Esercizio n. 24

Un generatore di tensione ha resistenza interna r = 600 Ω e f.e.m. uguale a 20 V.

Quale può essere la resistenza di un utilizzatore da collegare ai morsetti del generatore se la d.d.p. ai morsetti non deve essere inferiore all’80% della f.e.m.?

R: 2388 Ω ;

Esercizio n. 25

In un cantiere si devono sollevare carichi da 50 kg ciascuno a 20 m di altezza ma, per un guasto al sistema elettrico, è necessario ricorrere ad un motore a corrente continua alimentato da una batteria nuova di automobile da 12 V e 40 Ah.
Calcolare la potenza minima accettabile per il motore ed il numero di carichi che potranno essere sollevati prima di esaurire la batteria, sapendo che:
a) la batteria è nuova e perfettamente carica
b) il motore impiega un minuto per sollevare ciascun carico
c) il sistema ha un rendimento del 60%.
 

R: 272,5 W ; 105 ;

Esercizio n. 26

Una pompa solleva 100 litri di acqua al minuto all’altezza di 100 metri:
a) Calcolare la corrente che circola nel motore elettrico della pompa ad una tensione di 220 V
b) Se il motore ha un rendimento del 40% quale corrente circola?
 

R: 0,74 A ; 1,86 A ;

Esercizio n. 27

Qual è la resistenza di un filo di rame lungo 1 m che ha la sezione di 4,0 mm² se la resistività del rame vale 1,6∙10^–8 Ω∙m ?
 

R: 0,04 Ω ;

Esercizio n. 28

Il filamento di tungsteno di una lampadina è lungo 8,0 cm ed ha resistenza pari a 0,1 Ω.

La sua resistività vale 5,6∙10^-8 Ω∙m. Calcolare il diametro del filamento.
 

R: 239 mm² ;

Esercizio n. 29

Un orologio elettrico da 2,0 W, una radio da 4,0 W e due lampade da 100 W e 60 W sono simultaneamente alimentate dalla tensione di rete di 220 V.
Quanta potenza viene assorbita dalla rete?
Quanta corrente circola nella rete domestica?
 

R: 166 W ; 0,75 A ;

Esercizio n. 30

Quando si spende lasciando accesa per 36 ore una lampadina da 60 W se l’energia elettrica costa 0,19 €/kW∙h?

R: 0,41 € ;

Esercizio n. 31

In una casa vengono adoperati ogni giorno per due ore un sistema Hi-Fi da 200 W ed una stufa elettrica da 500 W e per quattro ore due lampadine da 60 W. Qual è il costo sostenuto in una settimana per gli oggetti elencati al prezzo di 0,19 €/kW∙h?

R: 2,5 € ;

Esercizio n. 32

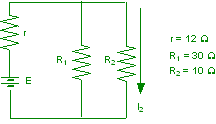
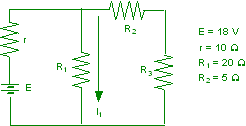
Nel circuito di figura determinare il valore della f.e.m. E affinché I₂ = 1,2 A.

R: 31,2 V ;

Esercizio n. 33

Nel circuito di figura determinare il valore da attribuire alla resistenza R₃ affinché la corrente che circoli nella resistenza R₁ sia

I₁ = 0,5 A.

R: 28,33 Ω ;

Esercizio n. 34

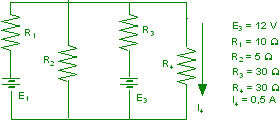
Nel circuito di figura, noti i valori di tutte le resistenze, della f.e.m. E₃ e della corrente I₄, determinare il valore della f.e.m. E₁.

R: 51 V ;

Esercizio n. 35

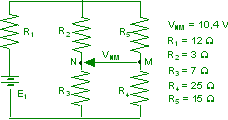
Nel circuito di figura, noti i valori di tutte le resistenze e della d.d.p. V_NM , determinare il valore della f.e.m. E₁.

R: 347 V ;