Nel 1713 venne pubblicata la seconda edizione
dei Principia. La prima risaliva al 1687, stampata in
numero limitato di copie sotto il titolo
Philosophiae Naturalis Principia Mathematica. Tra la prima e la seconda edizione erano
dunque trascorsi ventisei anni. Tanti anche
in un periodo assai meno frenetico dell'attuale.
Un tempo denso di eventi politici, culturali
e scientifici che avevano inciso in vario
modo nella vita dell'Inghilterra, dell'Europa,
di Newton e nelle sue relazioni sociali.
L'amicizia con il filosofo John Locke, probabilmente
una tra le più sincere e disinteressate tra
le poche coltivate realmente (1) - dato che
molte altre furono in qualche misura "sopportate"
o finalizzate a qualche utilità - costituiva
sicuramente quel tipo di "evento culturale"
che non lascia le cose come le trova. Tra
i due si era determinata, fino alla morte
di Locke nel 1704, un'affinità di vedute
sulle principali questioni di ordine filosofico
e teologico. Non era esattamente vero che
Locke e Newton si fossero occupati di questioni
radicalmente diverse. Convinto atomista,
il filosofo di Wrington aveva sviluppato
riflessioni sulla possibile influenza del
movimento fisico dei corpuscoli sulle idee
degli uomini. Era, dunque entrato nel merito
di questioni tradizionalmente assegnate al
dominio della filosofia e della teologia
in un modo che richiamava direttamente la
costituzione fisica del mondo. D'altro canto,
studiando la Bibbia, che anche Locke aveva
letto avidamente, Newton si era convinto
che il dogma Trinitario fosse stata un'invenzione
postuma dei filosofi cristiani e aveva inviato
una nota a Locke, che venne pubblicata solo
diversi anni dopo la morte di Newton. Simili
confidenze non si porgono al primo che capita
a tiro.
Entrambi avevano seguito una linea "politica"
di moderato e prudente anti-papismo ed osteggiato
le ingerenze cattoliche nella vita civile.
Un pericolo che aveva preso consistenza nel
periodo di re Giacomo ed era finito con lo
sbarco di Guglielmo d'Orange in Inghilterra
nel 1688. Per Newton, il "liberalismo"
propugnato da Locke aveva costituito un ombrello
protettivo, più filosofico che reale, contro
l'oscurantismo dell'Inquisizione che aveva
processato Galilei. Sia Locke che Newton
avevano condiviso la strategia delle "sensate
esperienze" inaugurata da Galilei e
detestato soprattutto la metafisica e la
fisica cartesiana, nonché l'assurda teoria
dei vortici di materia che sembrava costituire l'intelaiatura
di quelle elaborazioni. L'idiosincrasia di
Newton per le libere "fantasie"
si era condensata nel celebre motto Hypotheses non fingo, passato alla storia ed al vaglio della
critica più acuminata come una grande menzogna
metodologica. La verità, tuttavia, è che
Newton detestava realmente gli eccessi della
fantasia, essendo la realtà stessa assai
più ricca di ogni fantasia. Memore del detto
di Shakespeare nell'Amleto: "Ci sono più cose in cielo ed in terra
che nella tua filosofia!", Newton avrebbe
potuto applicarlo sia a Cartesio che a Leibniz,
come si vedrà.
In quel quarto di secolo, dunque, il pensiero
di Newton si era imposto e diffuso. Il trattato
sull'ottica, pubblicato nel 1704, era diventato
un punto di riferimento obbligato per tutti
coloro che pensavano di aver qualcosa da
dire in materia di trasmissione e ricezione
della luce. Newton era diventato un personaggio
rispettato anche oltre la ristretta cerchia
dei matematici e degli astronomi, ma non
si può dire che fosse anche amato. Si era
fatto, anzi, molti "nemici", o
meglio, era riuscito a suscitare con i suoi
comportamenti una rete di rancori e di invidie
che ben poco avevano a che fare con l'antipapismo
e l'Inquisizione. Già con la prima edizione
dei Principia, curata da Edmund Halley, agli occhi di
molti che conoscevano i retroscena, Newton
si era rivelato un ingrato nei confronti
ad esempio di Robert Hooke, che aveva invece
avuto molti meriti nella complessa vicenda
della costruzione della teoria. D'altra parte,
proprio Hooke, sollevando domande di chiarimento
alla Royal Society, ne aveva ritardato la data di pubblicazione.
Nel 1713, insomma, il contributo filosofico-scientifico
di Newton viaggiava a gonfie vele, ma egli,
come essere umano inserito in una comunità
di ricerca e in una società più vasta, rappresentava
un mezzo fallimento. Si chiacchierava del
suo "morboso" rapporto con il più
giovane Fatio, un elvetico sbarcato in Inghilterra,
più portato all'esibizionismo e alla ciarla
salottiera che alla meditazione scientifica.
Molti, e forse lo stesso Locke, avevano considerato
Isaac Newton un individuo con molti problemi
psicologici ed esistenziali.
La prefazione di Roger Cotes alla seconda
edizione
L'evento "scientifico",
ed anche
"culturale", costituito
dalla seconda
edizione dei Principia, non riguardava solo le precisazioni e le
sistemazioni di Newton, la più importante
delle quali si trovava nello Scolio generale che chiudeva il Terzo Libro, e di cui si
parlerà nel capitolo finale. Era di grande
interesse anche la prefazione scritta dal
matematico Roger Cotes, newtoniano d'acciaio.
Questi aveva diviso sommariamente gli studiosi
di fisica in tre categorie. I seguaci di
Aristotele costituivano il primo gruppo.
Gente che pretendeva di analizzare la natura
dei corpi, ma che ormai non aveva alcunché
da insegnare perché ragionava solo in termini
di "nomi delle cose" e non delle
"cose stesse". La seconda categoria
era costituita dai cartesiani. Costoro desideravano
eliminare le troppe complicazioni e ricondurre
tutte le spiegazioni ad una più ragionevole
semplicità. Questa stessa tendenza, li portava
ad esagerare, e quindi ad abbandonare la
realtà. Essi - scriveva Cotes - «cadono
nei sogni, in quanto hanno trascurato la
reale costituzione delle cose.» La terza categoria, l'unica ad aver scelto
la via giusta, secondo Cotes, seguiva la
lezione della filosofia sperimentale. Sono
coloro che «non assumono come principio
niente che non sia stato provato dai fenomeni.»
Newton, secondo Cotes, era stato il primo
ed il solo capace di dedurre «la spiegazione
del sistema mondo dalla teoria della gravitazione.»
L'aveva ricavata osservando il cielo e la
terra e come si comporta l'acqua messa in
un secchio appeso ad un filo, della qualcosa
si parlerà più avanti. Sarebbe stato meglio
precisare che Newton se l'era cavata, "leggendo
le osservazioni fatte dagli astronomi",
perché, in realtà, Newton osservava assai
poco; calcolava e speculava molto di più.
Non era certo stato un assiduo frequentatore
dell'Osservatorio di Greenwich, realizzato
- è bene ricordarlo - nel giugno del 1675.
Aveva il suo telescopio personale, tuttavia
non era assiduo e sistematico nell'impiegarlo.
Ma, l'entusiasta e fervido Cotes non andò
troppo per il sottile. D'altra parte, perché
negarlo: la teoria della gravitazione era
stata unicamente ricavata partendo dalle
osservazioni. O meglio, dalle osservazioni,
dal principio d'inerzia affermato da Galilei e sviluppato sul piano
speculativo delle ipotesi dal misconosciuto
napoletano Giovanni Alfonso Borelli (1608
- 1679). Questi, nel 1666, aveva fatto pubblicare
un trattato, il Theoricae mediceorum planetarium, nel quale asseriva che i pianeti si mantengono
nelle loro orbite a causa della combinazione
di tre forze: una «forza innata di
gravità», una forza tangenziale all'orbita
prodotta dalla luce del sole in rotazione,
una forza centrifuga che impedisce al pianeta
di cadere sul Sole. Lo stesso Newton riconobbe
la genialità di Borelli nel De mundi systemate, il Terzo libro dei Principia. Molto probabilmente, inoltre, Newton, si
era ancora avvalso delle Prutenicae tabulae, tavole astronomiche compilate da Erasmus
Rheinold (1511 - 1553), molto più precise
di tutte quelle precedenti, a conferma della
superiorità della visione copernicana che
trattava la Terra come corpo orbitante attorno
al Sole. (2)
Nell'attaccare i "cartesiani",
la prefazione di Cotes assumeva i caratteri
di un vero e proprio "manifesto filosofico"
costituito da una parte "anti"
e una parte "per". «Sento
- scrisse Cotes - che alcuni disapprovano
questa conclusione, e borbottano non so che
circa le qualità occulte. Sono soliti ciarlare
continuamente del fatto che la gravità specialmente
è un quid, e che, per la verità, le cause occulte,
debbono essere bandite dalla filosofia. Ma,
a costoro si risponde che cause occulte non
sono quelle la cui esistenza si dimostra
chiaramente per mezzo di osservazioni, ma
solamente quelle la cui esistenza è occulta
e inventata e ancora non è stata provata.
La gravità, dunque, non sarà dunque la causa
occulta dei moti celesti; se qualcosa, infatti,
è appalesato dai fenomeni, e che questo potere
esiste di fatto. Piuttosto, nelle cause occulte
si rifugiano coloro che propongono alla guida
di questi movimenti non so che vortici di
materia interamente immaginata e affatto
sconosciuta ai sensi.» Polemica contro
Cartesio, dunque, e ancor più, contro i cartesiani
del tempo di Newton , nostalgicamente persuasi
che i "vortici" fossero alla base
delle peripezie della res extensa. Rovesciare l'accusa è da sempre una via
percorribile in modo retorico.
Medice cura te ipsum. Via percorribile, finché regge. La spiegazione
cartesiana non reggeva più, né agli occhi
di Newton, né a quelli del fervido Cotes.
E soprattutto non spiegava come avvengono i fenomeni palesi.
Il paradosso di Descartes si potrebbe riassumere
così: dopo avere costruito una nuova matematica,
elaborò una fisica matematica senza matematica.
Il tono trionfalistico e irrìdente di Roger
Cotes, sotto questo profilo, non era del
tutto privo di una giustificazione.
Moto, tempo e spazio relativi ed assoluti.
L'esperimento del secchio.
I Principia sono organizzati in tre Libri. All'inizio
si trovano definizioni relative alla «quantità
di materia», alla «quantità»
di moto e alle «forze», unite
a considerazion raccolte in uno Scolio dedicato ai concetti di spazio, tempo e
moto. Sono definizioni ancora in uso attualmente.
Manca una definizione di momento angolare e l'enunciazione del principio della sua
conservazione. Questo potrebbe sembrare strano,
perché si tratta di uno dei capisaldi della
cinematica classica.
Per Newton occorre distinguere
tra spazio
assoluto e spazio relativo. Lo
spazio assoluto
è «per sua natura senza
relazione ad
alcunché di esterno,» e
«sempre
uguale e immobile.» Lo
spazio relativo
è la «misura dello spazio
assoluto»,
ossia il risultato di un'operazione
realizzata
dagli uomini.
Anche per il tempo valgono le
medesime affermazioni.
Pertanto, quando si ricorre al termine moto,
bisogna sempre distinguere tra movimento
assoluto e relativo. Il moto assoluto è «la
traslazione di un corpo da un luogo assoluto
a in un luogo assoluto», mentre il
moto relativo riguarda la traslazione da
punto relativo ad altro punto relativo. Per
distinguere si deve pensare a un individuo
collocato su una nave in movimento. Esso
si sposta sulla nave, la nave si sposta sul
mare, la Terra, di cui fa parte il mare,
si sposta nello spazio ruotando attorno al
Sole. Pertanto, è necessario stabilire il
moto vero della Terra nello spazio assoluto,
quindi è indispensabile un punto di riferimento
preciso, un luogo immobile. «I moti
totali e assoluti non si possono definire
che per mezzo di luoghi immobili [...]Ma
non esistono luoghi
immobili salvo quelli dall'infinito per l'infinito
conservano, gli uni rispetto
agli altri,
determinate posizioni; e così
rimangono sempre
immobili, e costituiscono lo
spazio che chiamo
immobile.»
Quindi, Newton è consapevole che ragionando
di «cose umane» si è spontaneamente
portati a considerare moti e luoghi relativi.
Per questo, aggiunge: «nella filosofia
occorre astrarre dai sensi.» Come si
può distinguere un moto relativo da uno assoluto?
Interviene una acutissima analisi circa «gli
effetti per i quali i moti assoluti e relativi
si distinguono gli uni dagli altri.»
I moti circolari vengono esemplificati con
l'esperimento del secchio rotante attorno
al proprio asse. «Se si fa girare su
se stesso un vaso appeso ad una corda, fino
a che la corda a forza di essere girata non
si possa quasi più piegare, e si mette poi
in questo vaso dell'acqua e, dopo aver permesso
all'acqua e al vaso di acquistare lo stato
di riposo, si lascia che la corda si srotoli,
il vaso acquisterà un moto che durerà molto
a lungo; all'inizio la superficie dell'acqua
contenuta nel vaso resterà piana, come era
prima che la corda si srotolasse, ma in seguito,
il moto del vaso comunicandosi poco a poco
nell'acqua contenuta, quest'acqua comincerà
a girare, a elevarsi verso i bordi ed a diventare
concava, come ho esperimentato; quindi con
l'aumentare del moto il livello dell'acqua
crescerà sempre più fino a che, concludendosi
le sue rivoluzioni, in tempi uguali ai tempi
impiegati dal vaso per fare un giro completo,
l'acqua sarà in riposo relativo rispetto
al vaso.»
La conclusione di Newton è che
il moto relativo
dell'acqua rispetto al secchio
non può giustificare
l'effetto inerziale dell'incurvamento
della
superficie dell'acqua (visto
che il moto
relativo è nullo e compatibile
sia con la
superficie piana sia con la superficie
curva
dell'acqua): ne viene che l'effetto
inerziale
è dovuto a un moto non relativo,
e quindi
a un moto rispetto allo spazio
assoluto,
il «vero e assoluto moto
circolare».
Il movimento dell'acqua «indica lo
sforzo di allontanamento dall'asse del moto,
e attraverso tale sforzo si conosce e viene
misurato il vero e assoluto moto circolare
dell'acqua.»
La conclusione è che lo scienziato
può superare
i limiti delle esperienze e considerare
solo
i moti relativi. Commentava:
«E' difficilissimo
in verità conoscere i veri moti
dei singoli
corpi e distinguerli di fatto
dagli apparenti:
e ciò perché le parti dello spazio
immobile,
in cui i corpi veramente si muovono,
non
cadono sotto i sensi. La causa
tuttavia non
è affatto disperata.»
Newton sostenne, insomma, che la deformazione
della superficie dell'acqua indicava che
era in azione una forza. La seconda legge
del moto - che viene esposta sotto - associa
forza ed accelerazione. Ma questa accelerazione
dell'acqua rispetto a che avviene? Newton
ne concluse che non è un'accelerazione relativa
al secchio, dato che essa assume forma prima
piana poi concava, allora dev'essere riferita
allo spazio assoluto. (3)
Assiomi o Leggi del movimento
Dopo le definizioni e lo Scolio, Newton introdusse
un gruppo di assiomi o leggi di movimento,
cui seguivano alcuni corollari. Essendo assiomi,
non c'era necessità di dimostrazione. In
un ulteriore Scolio, si limitò a commentare:
«Fin qui ho riferito i principi accolti
dai matematici e confermati da numerosi esperimenti.»
Il primo ed il secondo assioma, ad esempio,
erano già stati presentati da Galilei.
Legge I
«Ciascun corpo persevera nel proprio
stato di quiete o di moto rettilineo uniforme,
salvo che sia costretto a mutare quello stato
da forze impresse.»
Legge II
«Il cambiamento di moto è proporzionale
alla forza motrice impressa, ed avviene lungo
la linea retta secondo la quale la forza
è stata impressa.»
Legge III
«Ad ogni azione corrisponde una reazione
uguale e contraria: ossia, le azioni di due
corpi sono sempre uguali fra loro e dirette
verso parti opposte.»
Alle tre leggi seguono alcuni corollari.
Uno dei più densi di conseguenze è il cosiddetto
parallelogramma delle forze: «Un corpo
spinto da forze congiunte, descriverà la
diagonale di un parallelogramma nello stesso
tempo nel quale descriverebbe separatamente
i lati.»
Il moto dei corpi
Inizia ora l'esposizione del Primo Libro
dedicato al moto dei corpi. E' quasi completamente
svolto in termini matematici ed è presentato
come il «metodo delle prime ed ultime
ragioni col cui aiuto si dimostrano le cose
che seguono.»
Dopo l'esposizione di un insieme di Lemmi,
Newton avvisa che le dimostrazioni potrebbero
venir trattate seguendo il «metodo
degli indivisibili». Ma, vi ha rinuciato,
essendo via troppo ardua, anche perché «quel
metodo è stimato meno geometrico.»
E' lecito pensare che i Principia non siano un trattato di analisi infinitesimale,
ma è altrettanto lecito chiedersi se sarebbe
stata possibile, indipendentemente dai progressi
matematici realizzati da Newton (e da Leibniz)
una costruzione teorica di tale portata.
Lo stesso Newton spargeva un po' di briciole
sulla pista da lui seguita effettivamente
precisando: «Si obietta che poiché
non esiste l'ultimo rapporto di quantità
evanescenti, in quanto esso prima che le
quantità siano svanite non è l'ultimo, e
allorché svanite non c'è affatto. Ma con
lo stesso ragionamento si può giustamente
sostenere che non esiste la velocità ultima
di un corpo che giunga in un certo luogo.»
L'obiezione, secondo Newton, dovrebbe svanire
di fronte alla seguente argomentazione. «Per
velocità ultima si intende quella con la
quale il corpo si muove, non prima di giungere
al luogo ultimo nel quale il moto cessa,
né dopo, ma proprio nel momento in cui vi
giunge.» Ricorrendo all'analogia fisica,
Newton dimostra il concetto geometrico. «Similmente,
per ultime ragioni delle quantità evanescenti
si deve intendere il rapporto della quantità
non prima di diventare nulle e non dopo,
ma quello col quale si annullano. Parimenti,
anche la prima ragione delle quantità nascenti
è il rapporto col quale nascono.»
Il teorema IV della seconda sezione è quello su cui si
imperniano le principali deduzioni. «Le
forze centripete dei corpi che descrivono
cerchi con moto uniforme, tendono ai centri
dei medesimi cerchi, e stanno fra loro come
i quadrati degli archi descritti in tempi
uguali divisi per i raggi dei cerchi.»
Il teorema è accompagnato da corollari. Il
sesto afferma: «Se i tempi periodici
sono in ragione inversa della potenza 3/2
dei raggi e, per conseguenza, le velocità
inversamente proporzionali alla radice quadrata
dei raggi, le forze centripete saranno inversamente
proporzionali ai quadrati dei raggi e viceversa.»
Questo è proprio il caso dei corpi celesti.
La successiva sezione interessa i teoremi
che riguardano il moto dei corpi nelle sezioni
coniche eccentriche, e presenta la soluzione
di diversi problemi, tra i quali il seguente:
«Posto che la forza centripeta inversamente
proporzionale al quadrato della distanza
dei luoghi dal centro, e che sia conosciuta
la quantità assoluta di quella forza, si
ricerca la linea che un corpo descriverà
muovendo da un luogo dato con una velocità
assegnata secondo una data retta.»
La soluzione del problema evidenzia
che a
seconda dei valori assunti dalla
velocità
del corpo, questo potrà percorrere
un'ellisse,
una parabola, oppure un'iperbole.
Le rimanenti sezioni del primo libro trattano
altri argomenti di meccanica. Nelle sezioni
XII e XIII si parla di teoremi sulle forze attrattive
esercitate rispettivamente dai corpi sferici
e da quelli non sferici. Newton dimostra
che, dato «un corpuscolo» collocato
esternamente alla superficie di una sfera,
il corpuscolo «è attratto verso il
centro della sfera con una forza inversamente
proporzionale al quadrato della sua distanza
dallo stesso centro.»
Con ciò, Newton pensava di aver
posto i fonadamenti
matematici per una teoria soddisfacente
delle
interazioni gravitazionali.
Nell'ultima sezione del primo libro sono
brevemente affrontati i movimenti dei «corpi
piccolissimi», ossia quei moti che
provocano i fenomeni ottici della riflessione
e della rifrazione.
Avvertenza: i testi non cadono dal cielo come le mele
sulla zucca di Newton ma, si costruiscono
quotidianamente con un faticoso lavoro di
scrittura, preceduto da un appagante - ma
non meno faticoso - lavoro di lettura e scrematura.
Spesso ci si imbatte in testi noiosi, che
aggiungono assai poco.
In questo caso, si è approfittato di una
"intelaiatura" e ad essa si sono
aggiunte note, chiose, arricchimenti utili
di vario genere. Si è particolarmente utilizzato
l'impianto offerto dal saggio di Enrico Bellone
Isaac Newton
in (a cura di Paolo Rossi) Storia della scienza moderna e contemporanea - volume I - UTET 1988
Note:
1) Si veda la biografia romanzata
scritta
da Jean-Pierre Luminet - La parrucca di Newton - LA LEPRE edizioni 2011
2) Thomas S. Kuhn - La rivoluzione copernicana - Einaudi 1972
3) Considerazioni sul secchio e gli assoluti
Consigliamo chi legge queste
note di non
piantarsi sulle evidenti o presunte
difficoltà
ed obiezioni che potrebbero sorgere
in ogni
individuo desideroso di capire.
L'esperimento
in sé dimostra solo che esiste
un trascinamento
dell'acqua contenuta nel secchio,
non che
esiste un moto in uno spazio
assoluto e,
per di più, in un tempo assoluto.
Nulla impedisce
di immaginare un "tempo
ed uno spazio
vuoti di eventi" che si estendono ben al di là delle
regioni del cosmo visibili. Ossia di concedere
esistenza sostanziale al nulla o, se si preferisce, al vuoto. Ma, dove non c'è nulla, non c'è nemmeno
nulla da misurare. Per avere un tempo ed
uno spazio inclusivi di un tutto, bisognerebbe: i) accettare la teoria di
un unico Big Bang originario per tutto il cosmo; ii) essere
in grado di individuare nello spazio-tempo
il punto-momento esatto dell'evento. E' un
miliardo di volte più complicato che cercare
un ago in un pagliaio. La complicazione massima
è data dal fatto che non si sarebbe alla
ricerca di un punto materiale, una sorta
di pompa centrale ancora funzionante ma,
di un punto ormai senza dimensioni nell'infinità.
Tuttavia, costituirebe la possibiità, l'unica
sul piano logico, di avere un punto di riferimento
superiore - se non assoluto - rispetto al quale misurare tutti i movimenti e le successioni dall'origine
ai giorni nostri. Si tenga presente, inoltre,
che non è affatto esclusa la possibilità
di un cosmo inflazionario teorizzata da Andrei
Linde. Un cosmo, cioè, in cui, ora qui ed
ora là, germogliano big bang che danno luogo a vari ed innumerevoli universi.
Se si rinuncia all'impresa del ritrovamento
dell'origine, non resta che assoggettarsi
ad una disciplina matematica che consenta
di calcolare il movimento dei corpi materiali
in un sistema di riferimento dato.
Il bello del capitolo "Newton"
nella storia della fisica, è
che il suo sistema
di calcolo funziona in modo eccellente ancor oggi, indipendentemente
dalla querelle filosofica sull'esistenza di dimensioni spazio-temporali
assolute. Ci vollero oltre due secoli per
arrivare ad un superamento rivoluzionario,
con Einstein. Questi, tuttavia, scrisse:
« È necessario quindi, per giustificare la
necessità della propria scelta specifica
[di un sistema di riferimento], cercare qualcosa
che sia al di fuori di ciò che è oggetto
della teoria stessa (masse, distanze). Per
questa ragione Newton introdusse in modo
del tutto esplicito, come partecipante attivo
onnipresente in tutti gli eventi meccanici,
un elemento primario e determinante, lo "spazio
assoluto".» ( da Albert Einstein - Autobiografia scientifica - Bollati Boringhieri 1979)
Testi
Isaac Newton - Principi Matematici della filosofia naturale - Utet prima edizione 1965, ristampa 1997
Isaac Newton - Scritti di ottica - Utet, prima edizione 1978, ristampa 1997
Isaac Newton - Trattato sull'Apocalisse - Bollati Boringhieri 1994, 2011, trad.
e cura Maurizio Mamiani, (con testo a fronte)
Moses - dicembre 2012
| |
|
Roger Cotes
La "fisica" di Cartesio
Identità di Newton
Teoria binomiale
Serie di Newton-Mercator

La legge di gravitazione
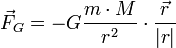
La formula su esposta non deve spaventare
chi da tempo è a digiuno di fisica,
oppure
che non l'ha mai studiata. Scritta
in questo
modo, persino Newton redivivo faticherebbe
a comprenderla. In realtà, vuol semplicemente
dire che la "gravità" non
è una
faccenda unilaterale. Un corpo attrae
l'altro
e viceversa. Quando facciamo un salto
in
alto, non è solo la Terra che attrae
il corpo,
ma è anche il corpo che attrae la Terra,
fatte le debite proporzioni.
Richard Feynman la espose così:«La
legge della gravitazione dice che due
corpi
agiscono l'uno sull'altro con una forza
che
varia in proporzione inversa al quadrato
della distanza tra loro, e che varia
in proporzione
diretta al prodotto delle loro masse.»
Se la scrivessimo così, avremmo un'idea
meno
complicata:
F = (G x m x m') diviso r2
ovvero:
F = forza gravitazionale
G = costante universale
m = massa del corpo 1, ad esempio la Terra
m' = massa del corpo 2, ad esempio la Luna
r = distanza
La formula può essere applicata a tutti
i
rapporti tra corpi celesti (Sole -
Terra;
Sole - Urano ecc...)
Rimase tuttavia aperto il problema del valore
numerico della costante universale "G".
I valori approssimati da Newton erano imprecisi
Qui si possono trovare interessanti spiegazioni
Ed anche qui
Come prosegue Feynman, «una costante
moltiplicata per il prodotto delle due masse,
diviso per il quadrato della distanza. Ora,
se aggiungo l'osservazione che un corpo reagisce
a una forza accelerando, ossia cambiando
ogni secondo la sua velocità in maniera inversamente
proporzionale alla sua massa, cioè che la
sua velocità varia di più se la massa è più
piccola, allora sulla legge di gravitazione
ho detto tutto quello che c'è da dire. Tutto
il resto è una conseguenza matematica di
queste due cose.» (Richard Feynman
- La legge fisica - Bollati Boringhieri 1971)

L'importanza di Isaac Newton nella
storia
della scienza
Si deve allora partire da qui per districare
l'apparente mistero del come mai i pianeti
seguano determinate orbite e non cadano dal
cielo sulla Terra o sul Sole. «Quando
- scrisse Kuhn - Newton affrontò il problema,
attorno al 1666, riuscì a determinare matematicamente
la velocità alla quale un pianeta deve "cadere"
verso il Sole oppure la Luna verso la Terra,
per rimanere in un'orbita circolare stabile.
Poi, dopo scoperto come variasse questa velocità
matematica di caduta con la velocità del
pianeta e con il raggio della sua orbita
circolare, Newton fu in grado di dedurre
due conseguenze fisiche di estrema importanza.
Se la velocità dei pianeti e i raggi delle
loro orbite erano legati tra loro dalla terza
legge di Kepler, Newton trovò che l'attrazione
che guidava i pianeti verso il Sole doveva
diminuire in misura inversamente proporzionale
al quadrato della distanza che li separava
dal Sole. A distanza doppia dal Sole, un
pianeta avrebbe bisogno solo di un quarto
della forza di attrazione necessaria per
farlo rimanere nella sua orbita alla velocità
con cui viene osservato.
La seconda scoperta di Newton fu egualmente
di grande portata. La stessa legge
quadratica
di proporzionalità inversa, egli trovò,
avrebbe
potuto benissimo spiegare la differenza
di
velocità con cui cadono verso la Terra
la
Luna lontana ed una pietra contigua.
Tredici
anni più tardi, riportato al problema
da
una controversia con Hooke, generalizzò
ulteriormente
i suoi risultati e dimostrò che una
legge
quadratica di proporzionalità inversa
poteva
spiegare esattamente sia le orbite
ellittiche
specificate dalla prima legge di Kepler
sia
la variazione di velocità descritta
nella
seconda.Queste deduzioni matematiche non avevano
precedenti nella storia della scienza.»
(T.S. Kuhn - La rivoluzione copernicana)
Leggi di Kepler
Come tornare da Newton a Kepler
Sistema di riferimento
Ascesa e caduta della fisica classica
(da wikipedia, l'Enciclopedia galattica)
«Con il nome di fisica classica si
raggruppano tutti gli ambiti e i settori
della fisica che non fanno uso né della relatività
generale, né di teorie quantistiche. Per
tale motivo è possibile classificare come
fisica classica tutte le teorie prodotte
prima del 1900, l'anno in cui Max Planck
pubblicò i primi lavori basati sull'ipotesi
dei quanti. Alcune teorie successive, come
la relatività ristretta, possono essere considerate
classiche o moderne. Sono quindi comprese
le teorie sulla meccanica, inclusa l'acustica,
sulla termodinamica, sull'elettromagnetismo,
inclusa l'ottica, e la gravità newtoniana.
La fisica classica ricomprende teorie
che
avevano avuto la loro origine già prima
della
nascita del metodo scientifico, anche
se
fu solo dopo la codifica di quest'ultimo,
attribuita a Galileo Galilei, che si
ebbe
la maggior parte delle scoperte. Già
prima
delle scoperte galileiane, infatti,
e fin
dall'inizio delle prime civiltà, l'uomo
aveva
iniziato a indagare la natura, seppur
utilizzando
metodi non necessariamente basati sul
confronto
diretto con l'esperienza e, per questo,
più
speculativi.
A seguito dei lavori dello scienziato
pisano,
si aprì una fase di indagine approfondita,
che si sviluppò a partire dai problemi
meccanici,
con particolare attenzione verso la
meccanica
celeste, attraversata dal confronto
fra la
teoria geocentrica e quella eliocentrica.
La curiosità della comunità scientifica
si
estese poi ai fenomeni elettrostatici
e magnetici,
con la formulazione del concetto di
carica
elettrica, termodinamici e infine elettrodinamici.
Non bisogna dimenticare, nel definire
la
storia dello sviluppo di questa particolare
branca della fisica, che i suoi molti
settori
attuali si sono evoluti parallelamente
nel
corso del tempo e hanno subito più
volte
scissioni e ricombinazioni fino ad
assestarsi
con le suddivisioni oggi comunemente
accettate.
Ad esempio l'attuale elettromagnetismo
classico
è frutto dell'unificazione di elettricità,
magnetismo e ottica, operata grazie
alla
sintesi matematica che ne fece James
Clerk
Maxwell.
Fu proprio grazie agli studi di Maxwell
che
si posero le basi perché la fisica
classica
entrasse in crisi. Lo studio della
forma
dello spettro di corpo nero, l'impossibilità
di spiegare termodinamicamente il comportamento
del calore specifico a bassissime temperature,
la scoperta di fenomeni come l'effetto
fotoelettrico,
e perfino la formulazione stessa delle
equazioni
di Maxwell generavano una serie di
contraddizioni
che in breve tempo mise in crisi il
complesso
apparato della fisica classica, e portò
alla
formulazione della relatività speciale
prima
e della meccanica quantistica successivamente.
Infine è necessario ricordare che fu solo
grazie al progressivo sviluppo della matematica
che fu possibile l'evoluzione di nuove teorie
fisiche che necessitavano di nuovi strumenti,
come il calcolo differenziale, per poter
essere studiate. Infatti la storia della
fisica classica è intrecciata con quella
della matematica, da cui attinse e al cui
impulso contribuì non poco, per lo meno a
partire da quando i fisici accettarono come
conveniente il servirsi di formule matematiche
per sintetizzare le proprie teorie». |
