Volpi e conigli,

ovvero predatori e prede,che convivono in uno stesso habitat, fra loro in perenne conflitto e insieme perennemente alleati per sopravvivere.
Se le volpi uccidono troppi conigli,questi rischiano di estinguersi, ma allora anche le volpi, rimaste senza cibo, li seguiranno nella stessa sorte.Però il calo del numero di predatori può salvare i conigli dall' estinzione.
Se i conigli uccisi sono  troppo pochi, il loro numero rischierà di crescere a dismisura e le risorse ambientali potranno diventare insufficienti;tuttavia, se anche le risorse fossero illimitate,
le due popolazioni forse non crescerebbero indefinitamente: la maggior disponibilità di cibo farebbe aumentare anche le volpi, ma in tal caso anche la predazione aumenterebbe e la crescita della popolazione dei conigli subirebbe un rallentamento, se non addirittura un' inversione.
La dinamica della convivenza conflittuale di due specie in un ambiente appare dunque piuttosto complessa,anche quando le risorse siano illimitate e l' ambiente  chiuso, ma la costruzione di modelli che, sia pure informa molto semplificata e un po' astratta,ne sappiano cogliere degli aspetti significativi, non richiede particolari competenze ed è quindi accessibile a tutti.
Val quindi la pena di occuparsene, tanto più che si tratta di una situazione emblematica: ne esistono infattimolte altre, rette anch' esse da meccanismi di feedback ,che si lasciano descrivere negli stessi termini.

L' iniziatore di questo filone di ricerche fu Vito Volterra, il quale, dopo aver conosciuto di un biologo,  si mise a studiare queste cose e  ben presto elaborò un modello matematico della dinamica 'preda-predatore',sotto forma di equazione differeziale.

Qui ne verrà presentata una versione ' discreta', concettualmente più accessibile .
Il modello differenziale ha dalla sua il pregio di essere più gestibile dal punto di vista dei calcoli formali, ma ora, grazie al computer, anche le equazioni discrete si lasciano maneggiare assai più agevolmente che in passato.Il loro esame numerico e grafico può rendere trasparenti proprietà che la loro forma da
sola non  mette in luce, a differenza di quel che avviene a volte  con le equazioni differenziali.

Ma passiamo ai fatti.

Una prima modellizzazione

    Indichiamo con     x     il numero dei conigli

                          y    il numero delle volpi

La coppia (x,y) è uno stato del processo di convivenza, rappresentabile con un punto del piano cartesiano e
una curva è un processo. Si tratta di esaminare la forma di questi processi.

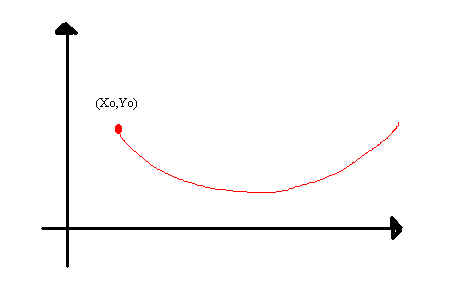
Costruiamone uno, in modo qualitativo, partendo da uno stato iniziale (x_o,y_o), con pochi conigli, insufficienti per nutrire le volpi. Le volpi diminuiranno e i conigli, sottoposti ad una minor predazione, cominceranno a riprendersi, ma dopo un po' l' accresciuta disponibilità di cibo per le volpi, attenuerà il declino della loro specie.

Se mettiamo in un grafico tutto ciò otteniamo un pezzo del processo interattivo.

Dal modello qualitativo a quello quantitativo

Anzitutto complichiamo un po' i simboli.

Indichiamo con    x_n   il numero dei conigli all' istante n

( o, se preferite,  nel giorno n, nel mese n ...).

Idem per il numero di volpi.

A questo punto possiamo ipotizzare un modello del tipo:

                    VARIAZIONE DEI CONIGLI  [nel mese n]

                                              ||

                      CONIGLI NEONATI[nel mese n]

                                          meno

                     CONIGLI MANGIATI[nel mese n]+

   CONIGLI MORTI PER CAUSE NATURALI[nel mese n]

                  VARIAZIONE DELLE VOLPI[nel mese n]

                                            ||

                   VOLPI   NEONATE[nel mese n]

                                         meno

    VOLPI MORTE PER CAUSE NATURALI[nel mese n]

Passiamo ai simboli.

O anche , mettendo le equazioni in forma normale:

A, B, C, D sono costanti del modello, su cui torneremo. Ora interpretiamo le due equazioni, riferendoci alla prima coppia, che traduce con ipotesi ragionevoli le due condizioni scritte in forma verbale.

I termini lineari ( quelli di coefficienti a₁, a₂ e c) non hanno bisogno di commento.

Il termine rettangolare della 1° equazione istituisce un legame di proporzionalità fra il numero dei conigli mangiati da un lato  e quello dei conigli e delle volpi esistenti ( diciamo, all' inizio del mese) dall' altro.

Il termine rettangolare della 2° equazione istituisce un legame di proporzionalità fra il numero delle volpi neonate da un lato  e quello dei conigli e delle volpi esistenti ( diciamo, all' inizio del mese): si dà quindi importanza alla relazione fra prolificità ( e mantenimento della prole ) da un lato   e disponibilità di cibo dall' altro.

Ed ora qualche osservazione sulle costanti.

Riflettendo sul loro ruolo e tenendo conto di queste relazioni ,può essere ragionevole prendere

                                                       A fra 1  e 2           

                                  B,C,D fra 0 e 1

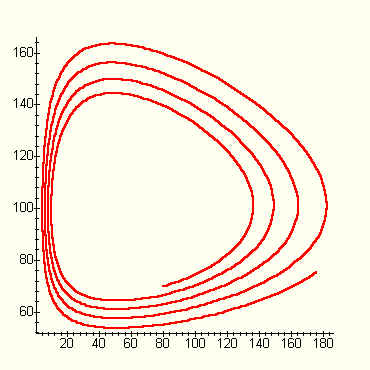
Ecco il processo ottenuto con 70 volpi e 80 conigli iniziali, A=1.1, B=0.001, C=0.99, D=0.0002, con 900 iterazioni:

Lo stesso con 5000 iterazioni.

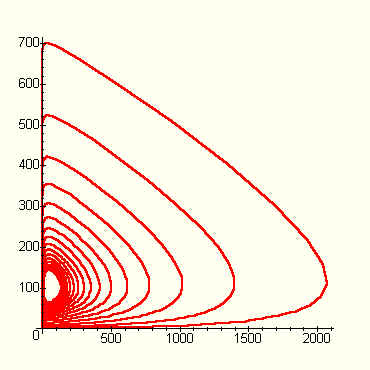
Il processo è pressappoco una curva chiusa che si va allargando col passare del tempo: sembra un ciclo che si ripete , con i conigli e le volpi che rischiano sempre di estinguersi, ma poi si salvano sempre in extremis e alla lunga diventano sempre più numerosi.

Naturalmente il lettore interessato può giocare con i parametri e sviluppare la cosa per conto proprio,trovando magari altre situazioni interessanti.

Ecco il listato in Maple del programma ( facilmente trasferibile ad altri linguaggi).

                               COSTANTI

> A:=1.1;B:=0.001;C:=0.99;F:=0.0002;

> numero_iterazioni:=900;

                         CONDIZIONI_INIZIALI

> x(0):=80;y(0):=70;

                                CICLO

> for n from 0 to numero_iterazioni do
> x(n+1):=A*x(n)-B*x(n)*y(n):
> y(n+1):=C*y(n)+F*x(n)*y(n):
> od:

                               GRAFICO

> curva:=[seq([x(j),y(j)],j=0..numero_iterazioni)]:
> plot(curva);

Per il programma in Excel, clicca qui .

Inversioni di tendenza

Il calcolo delle inversioni di tendenza   può essere fatto in questo modo.

Facendo n+1=n nella 1° equazione, si ottiene l' ordinata dei punti a tangente verticale, cioè quante sono le volpi quando c' è una inversione di tendenza fra i conigli ( in matematica ci si riferisce a quell' ordinata come ad un punto stazionario per la crescita dei conigli)

                               ( A-1)/B

Operando in modo analogo sulla 2° equazione si ottiene l' ascissa dei punti a tangente orizzontale, cioè il punto stazionario per la crescita delle volpi

                                 (1-C)/D

Uno sguardo alla prima figura lo conferma ( (A-1)/B=50,  (1-C)/D=100) ).

Un esame grafico più accurato mostra che la crescita  delle popolazioni avviene in maniera esponenziale, nel senso che la sequenza dei massimi della popolazione dei conigli, per esempio, è interpolata nel tempo da una curva esponenziale o almeno così pare che accada con i valori numerici considerati sopra.

Nel grafico che segue compaiono due curve- ottenute con Maple: quella oscillante rappresenta l' andamento  della popolazione dei conigli nel tempo ( legge oraria), l' altra è l' esponenziale .

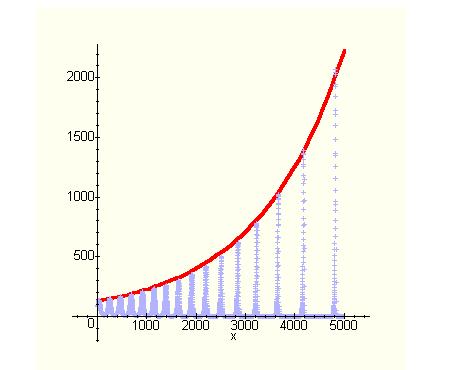
E' curioso che le l' evoluzione delle due specie in conflitto alla lunga segua lo stesso corso che si avrebbe se fossero separate, obbedendo appunto, pur con alti e bassi, ad una legge di tipo esponenziale.