.In 1913 Niels Bohr proposed a new revolutionary model of the atom by combining the Planck’s and Einstein’s researches into the light with the Rutherford’s model of the atom.
In order to overcome the difficulties connected with the Rutherford’s model he added to the classical Physics some new quantum conditions (known today as Bohr’s postulates) completely in contrast with the knowledge of his time.
First Bohr’s postulate states:
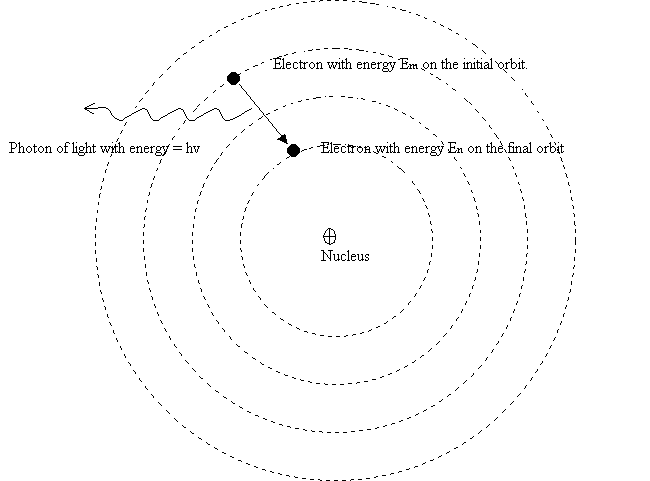
In the atom, electrons can turn around the nucleus only following some particular circular orbits and they do this without emitting energy. (stable orbits).
Each stable orbit has a definite energy .
Second Bohr’s postulate states:
An atom emits, under the form of light, the energy 
only when an electron jump from an higher energy orbit to a lower energy orbit .
This emitted energy is equal to the difference between the energies of the two orbits involved in the jump.
By looking at the diagram this means:
Bohr developed his predictive model for the hydrogen atom.
It is the simplest atom: it has a nucleus made of one proton and it has just one orbiting electron, hence it is quite easy to describe such a system using the physics rules.
Bohr started from the classical Newton’s equation.
is the mass of the electron.
is the Coulomb’s attractive force between the proton of the nucleus and the electron.
In this formula:
is the electron charge
is the proton charge.
is the Coulomb’s constant.
is the distance between the proton and the electron and it represents the orbit radius.
is the centripetal acceleration experienced by the electron while turning round the nucleus.
In this formula
represents the velocity of the electron.
In This way he wrote the classical motion equation for the electron in the hydrogen atom:
At this point he introduced a new Quantum limit represented by a third postulate:
Third Bohr’s postulate:
The Angular Momentum of the electron 
in the atom, can assume only multiple values of the Planck’s constant 
divided by 
:
Third postulate (2)
(
is an integer
number that can have the values and
so on.)
By writing a mathematics system between the classical motion equation (1) and the third postulate (2), Bohr discovered the radius of the possible quantum orbits for the electron in the atom:
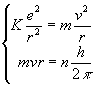
By solving this system, he found out the radius of the stable orbits of the electron.
(3)
and so on….
Unfortunately the radii of the orbits can’t be physically observed, only the energies emitted from the atom can. Hence, in order to have an experimental confirmation of his model, Bohr computed the energies of every single orbit too. To do this, he combined the classical considerations about the energy with the last quantum condition about the orbit’s radii (3).
He found out that energies behave this way:
(4)
where 
is the energy of the smallest orbit
in the atom. (eV means electron-volts, a particular unit of measurement of the
energy)
The energies of the other orbits are
and so on…
As we can see, the bigger are the radii of the orbits, the bigger become the energies (energies become less negative). This is an expected fact: the electron needs more energy to jump to a farer orbit because it has to win the electrostatic attraction of the nucleus.
When we supply energy to the hydrogen atom, the electron can absorb it: in this case it jumps towards a more external orbit because it has a surplus of energy.
If we stop to supply energy, after a bit, the atom comes back to its normal state and jump towards the more internal orbits by emitting energies under the form of light (photons), see the java applet at http://www.colorado.edu/physics/2000/quantumzone/lines2.html.
The second Bohr’s postulate said us that the energy of the emitted photon is equal to the difference between the energy of the orbits involved in the electron jump.
For example, by jumping from an higher energy orbit 
towards a lower energy orbit 
,the
electron emits one photon of light with energy
by replacing 
in this equation with the
(4) equation, we have
and if we write the frequency 
as a function of the wavelength of the photon 
(
that implies 
)
we have
As shown, The Bohr’s model can exactly explain the energy emitted by the atom and its line spectrum.
Bohr’s accomplishment was to build a model by combining different ideas available at his time:
Bohr was not seized with fright to build a model in which some new quantum conditions are superimposed to the classical motion equations. With his work, he definitively undermined the role of the Classical Physics: The whole universe can’t be described by using only the Newton’s physics equation and his classical consequences.
