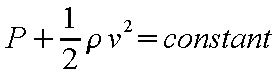
Bernoulli's principle
The principle can be regarded as the principle of the conservation of energy applied to fluids. Talking about fluids, the conservation of energy is referred to a given volume of it and the resulting statement is always referred to the density of energy, that means the energy per unit volume of fluid. The principle states that if a change in the density of energy within the fluid occurs, the fluid moves from a point to another developing a kinetic energy per unit volume exactly equal to the change occurred; this way the total energy is conserved and remains constant. Since the density of energy in a fluid is merely the pressure of the fluid, any change in pressure provokes a fluid acceleration from the region of higher pressure towards the region of lower pressure. Thinking for instance to a moving fluid which is flowing horizontally in a pipe, the statement takes the form: the sum of the pressure plus the kinetic energy per unit volume of the fluid remains constant.
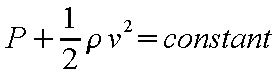
In the previous relation “P” is the pressure of the
fluid,
![]() the
density of the fluid, “v” the velocity of the fluid. The
relation points out that in order to keep the sum constant the
pressure must be larger when the fluid speed is smaller and
viceversa. Combining Bernoulli's principle with the conservation of
the rate of flow in a pipe, pressure conditions in a pipe can be
easily deduced: the pressure decreases along the constrictions of the
pipe while increases where the cross sectional area of the pipe
becomes larger (read the text on page 172). The same principle
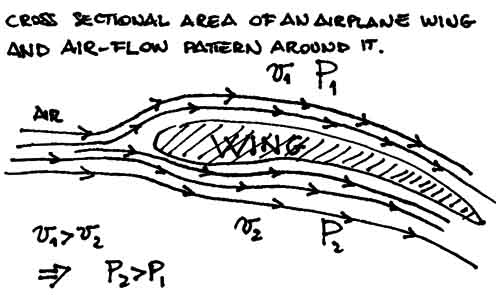
explains how airplanes fly. The shape of an airplane wing is such as
to cause a greater speed of the air flowing over the wing and a
smaller speed of the air flowing underneath. As a consequence, the
pressure under the wing is larger than the pressure over the wing
resulting in a net force pushing upward and letting the plane
floating in the fluid. (read the text on page 173).
the
density of the fluid, “v” the velocity of the fluid. The
relation points out that in order to keep the sum constant the
pressure must be larger when the fluid speed is smaller and
viceversa. Combining Bernoulli's principle with the conservation of
the rate of flow in a pipe, pressure conditions in a pipe can be
easily deduced: the pressure decreases along the constrictions of the
pipe while increases where the cross sectional area of the pipe
becomes larger (read the text on page 172). The same principle
explains how airplanes fly. The shape of an airplane wing is such as
to cause a greater speed of the air flowing over the wing and a
smaller speed of the air flowing underneath. As a consequence, the
pressure under the wing is larger than the pressure over the wing
resulting in a net force pushing upward and letting the plane
floating in the fluid. (read the text on page 173).