Fluids in motion: rate of flow and viscosity

Talking about fluids in motion, the speed of the current varies from point to point in a stream and different behaviors take place depending on the width of the stream. Where the stream is narrower the flow is faster, where the stream is wider the flow is slower. Furthermore the speed is larger in the middle of the stream than close to the banks.
These features can be explained by introducing the concepts of rate of flow and viscosity.

Rate of flow
The rate of flow and its conservation are easy to be understood by referring to water while moving through a pipe. If the flow is continuous, in a given time the same amount of water passes the cross sectional area of the pipe at different point. In other words, if no waste takes place, the rate of flow remains constant all along the pipe.
From the physical point of view the rate of flow is the volume of water flowing in a given interval of time divided by the same interval of time, as a consequence its unit of measurement is meter cubed over second.

A given volume of water could also be written by introducing the cross sectional area “A” multiplied by a given length “l” of the pipe. (See the figure)

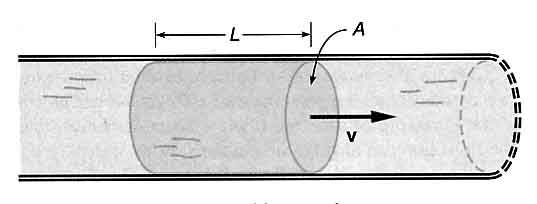
Hence the rate of flow could also be expressed this way:

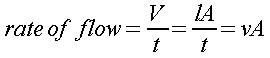
where “v” is the velocity of the fluid in the pipe.
By summarizing the previous considerations, the rate of flow remains constant and it can be stated shortly by writing:

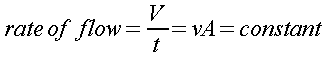
This simple law explains how the changes in speed of the water are related to the section of the pipe: because the rate of flow remains constant the velocity of the water must increase where the cross sectional area decreases and vice-versa.

Viscosity
Viscosity accounts for frictional effects between different layer of fluid. Actually, if we imagine fluid as made up of layer, each layer moves more slowly than the layer immediately above. Consider for example a trough, since its bottom is not moving it exerts a friction on the bottom layer of the fluid which is the slowest, this layer exerts a frictional drag on the layer immediately above which, anyway, is faster than the bottom layer because it's not directly in contact with the bottom of the trough, this second layer flows more slowly then the third layer immediately above and so on (see the figure above).

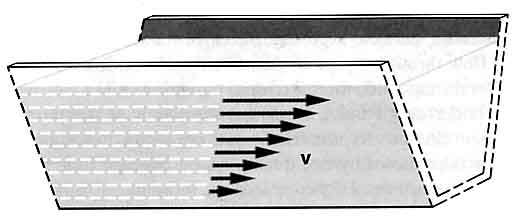
Viscosity is defined by the magnitude of the frictional forces between the layers of fluids. In general the layer that is in contact to the bottom or to the walls of a pipe doesn't move at all, The fluid speed increases as the distance from the wall increases. The variation of speed with distance depends on the viscosity and, indeed, on the rate of flow of the fluid through the pipe. For a fluid with a low viscosity the transition to the maximum speed occurs over a short distance from the wall (see the figure above).

Viscosity of fluids differs from substance to substance, but in general liquids have higher viscosities than gases and the viscosity changes enormously with temperature. The higher the temperature, the lower the viscosity for a given fluid (heating honey for instance make it less viscous and makes it spread more easily).

Laminar and turbulent flow
When the flow of a fluid is smooth and laminar and there are no eddies or other turbulences, the flow is called “laminar flow” and it can be described by ideal parallel streamlines that indicate the direction of the flow at any point (See the figure).

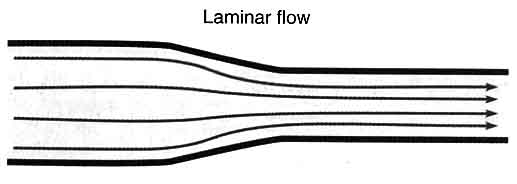
On the contrary when streamlines disappear while whorls and eddies appear the flow becomes turbulent. (see the figure).

When the flow is turbulent the resistance within the fluid highly increases; the transition from laminar to turbulent flow depends on the velocity of the fluid, and on the viscosity. Higher velocities tend to produce turbulent flow while, on the other hand, higher viscosities inhibit it. The transition from laminar to turbulent flow can be observed for example at the narrowing of a stream or in the smoke rising from a candle, so as in other common phenomena.