Experimental evidence suggest that magnetic forces are exerted by magnets on other magnets, by current-carrying wires on each other and by magnets on current carrying wires. A much deeper analysis shows how a wire of length "l" subjected to a magnetic field "B", experiences a torsion force when a current "I" flows in it.
The magnitude of this force is
where "alfa" represents the angle between the direction of the field B and the direction of the current in the wire. Because of the "sin" function dependence, the force is exactly
only if the wire and the direction of the field are perpendicular to one another (alfa=90°). The force experienced by the wire decreases when alfa decreases, the force vanishes when alfa becomes zero, that is when the wire is parallel to the field: as a matter fact, a current-carrying wire parallel to the magnetic field lines doesn’t experience any force.
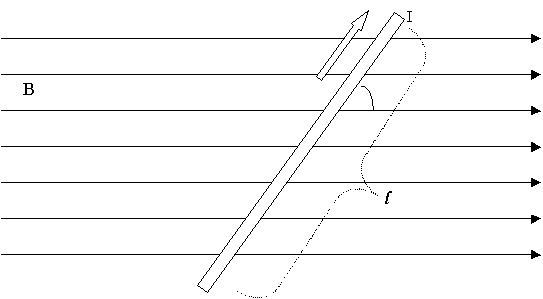
The direction of the force is perpendicular to both the electric current and to the magnetic field. This direction can be computed by using the right hand rule: if you point the thumb of your right hand in the direction of the current, the index finger in the direction of the field, the middle finger points and indicates the direction of the resulting force on the wire (for instance in the drawing above, the resulting force points into the page).
Such a phenomenon when connected to the meaning of electric current, suggests a more general fact: "a magnetic force is exerted on a moving charge". An electric current represents a movement of charged particles, hence, from the microscopic point of view, the previous law referring to a single "q" charged particle, takes the form:
(Lorentz force)
where "v" is the speed of the particle while travelling in a region where a "B" field exists. (see the figure above)
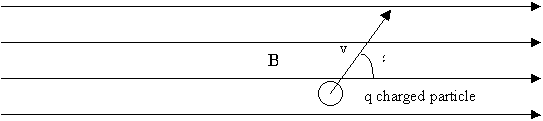
As before, the magnitude of the force on the particle has its maximum value
when the particle travels perpendicular to the field (alfa=90°), while the
direction of this force can be computed with the right hand rule again. The
thumb points in the direction of the particle velocity vector, index and middle
finger have the same value as before.
Note that if we reverse the previous formulas we can identify the magnetic field as a function of the magnetic force it produces:
or
From these definitions we can deduce the unit of measurement of the magnetic field:
the unit is equal to one Newton per Ampere-meter which is shortened to "Tesla". next...