Empirical evidence (for example pith-balls, the leaves of the
electroscope,
etc.) demonstrates that electric charges exert a force on one another.
Charles Coulomb (1736-1806) was the man who discovered how this force depends on
the amount of charges and on the distance between them.
He investigated the problem and measured the weak forces between charges by
using a torsion balance like the one in the figure (take a look in the textbook
on page 229 for a more detailed description of the experiment).
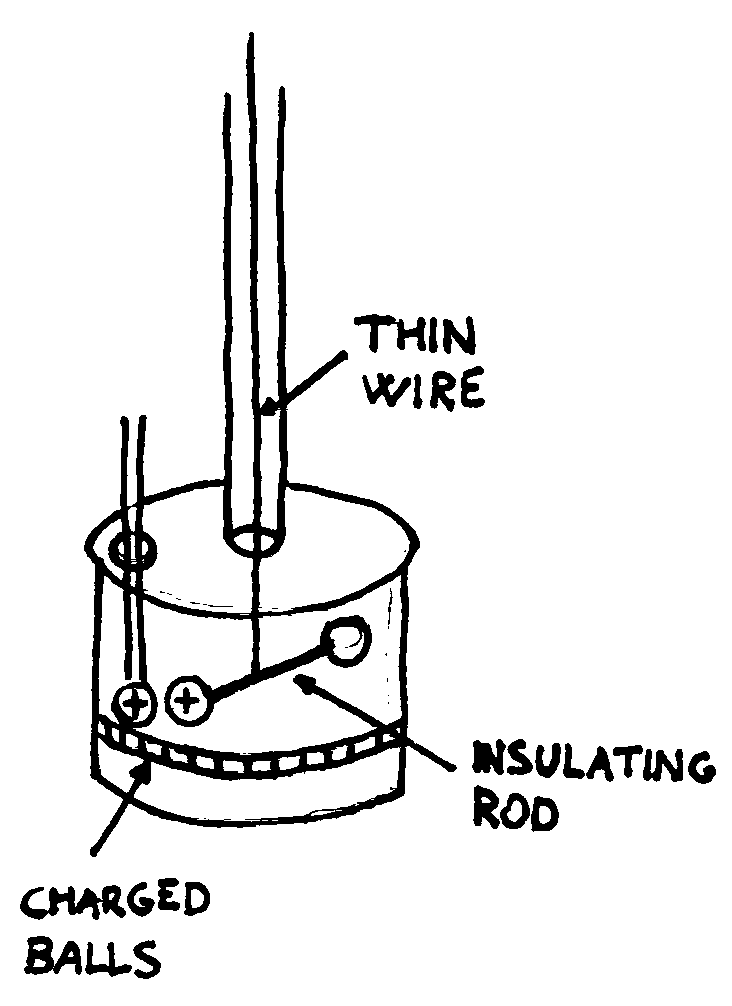
The torsion balance consists of two metal balls that are balanced on an
insulating rod suspended at the middle point from a thin wire.
A force applied to one of the two balls produces a torsion of the wire (it
twists). Hence, by previously establishing how much force is necessary to twist
the wire at a certain angle, we have a method of measuring weak forces.
To measure the electrostatic force we charge one of the two balls, then we
insert near it a third ball with the same charge. The two balls repel each other
and the wire twists. By varying the distance between the two charged balls, the
strength of the force between them at different distances can be measured.
This way we can measure the dependence of the electrostatic force on distance
for a given quantity of charge on the two balls.
On the other hand, to understand how the force depends on the quantity of charge
at a given distance, Coulombs had to solve the problem of how to place different
and known quantities of charge on the two metal balls. To do this, he thought up
a charge division method as described in the textbook at the end of page 229.
With this method he discovered how the force depends on the charges in relative
terms.
The result of his work can be summarized by saying that the electrostatic force
between two charges, named 
and 
,
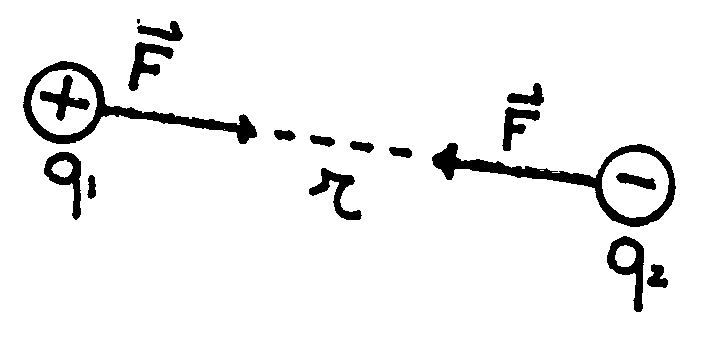
is directly proportional to the amount of them, while it is inversely
proportional to the square of the distance 
:
The symbol 
means
that the direction of the force is along the line connecting the two charges.
In other words, we can express the strength of the force simply by writing
where
is the
proportionality constant that allow us to write the previous equality.
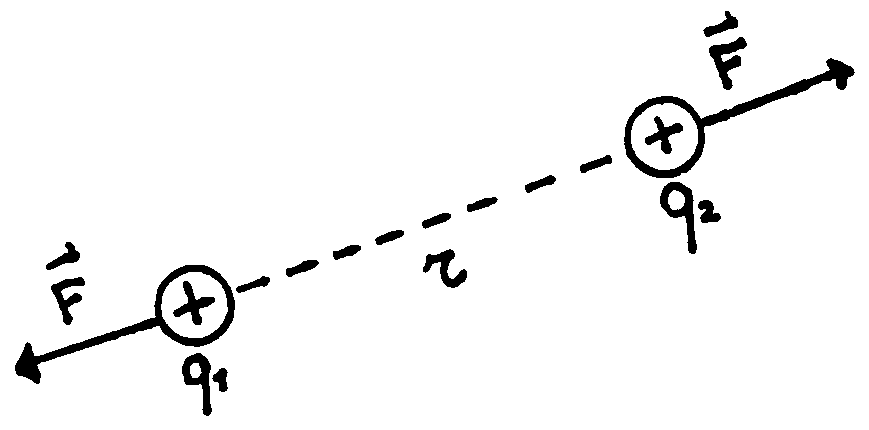
Notice that the 
unit of
measurement involves the 
that is the unit of measurement of the charge. For a better understanding of
Coulomb’s law, take a look at the following
exercises.