and
kinetic energy 
is a quantity that remains constant in all situations where there are no forces
doing work on a system. We call this sum Total Mechanical Energy 
.The sum of potential and
kinetic energy
is a quantity that remains constant in all situations where there are no forces
doing work on a system. We call this sum Total Mechanical Energy .
Total Mechanical Energy.
The essence of the principle can be written this way:
If 
then 
In other words, if no forces disturb a physical system the mechanical energy
of such a system conserves itself.
In order to understand the principle, we can examine three different situations.
A pendulum consists of a ball hanging at the end of a string attached to a fixed support. (figure below).
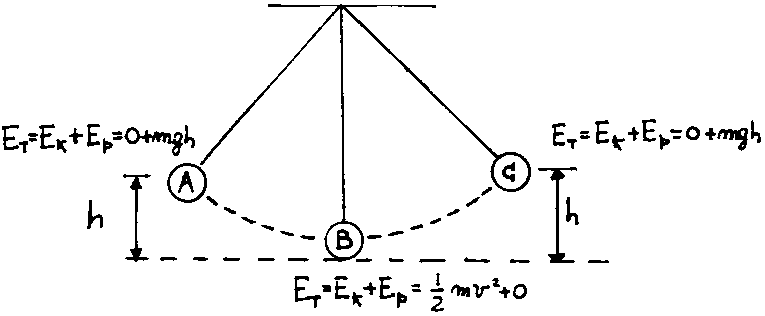
When we pull the ball to one side we do work on the system; we increase the
total energy of the system and in particular we increase the potential component
of the energy to a value 
where "h" is the height from the equilibrium position. (look at point
"A" in the diagram).
When we release the ball, the oscillations start: the potential energy
converts to kinetic energy. At the bottom point "B" the potential
energy will be zero and the kinetic energy will reach its maximum value. When
the ball overshoots this position, it slows down while the relative distance
from the ground line increases. During this period, the kinetic energy is
converted to potential energy until the ball reaches the opposite position
"C". At the point "C" the ball is at rest for a single
instant. At that instant the kinetic energy is zero and the potential energy has
the value
again. Then, the swinging starts again and the conversion between the potential
and kinetic energy repeats and continues as the pendulum oscillates back and
forth.
Of course, our pendulum represents an ideal system, because in a real one, frictional forces like air resistance act. As time passes the frictional forces reduce, consume and spend, the total energy of the system; as a result the amplitudes of the pendulum oscillations decrease until the pendulum stops. In any case the ideal pendulum is a good example of a system where a conversion among potential and kinetic components of energy takes place.
Imagine a cyclist starting to "climb" the hill sketched in the diagram.
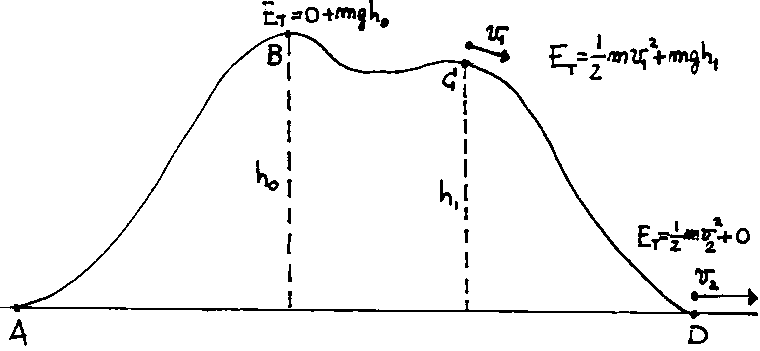
From point "A" to point "B" the cyclist will work against
the gravitational force in order to change his altitude from the ground to the
top of the hill. There, he stops to rest and have a snack. From the Mechanical
point of view, the energy of the system is now higher because work is being done
against gravity in order to move the system from the ground to an 
height. The potential energy is now increased to a value 
.
The kinetic energy is zero because the cyclist is at rest. At point
"B" the total energy is completely a potential energy. After a bit,
the cyclist throws himself down the hill and gains velocity and when he passes
point "C" his total energy is always the same as point "B",
but this energy is now partially distributed into two components: a kinetic
component because he passes point "C" with a 
velocity, a potential component because the "C" point is at an 
height
from the ground. From point "C" to point "D" the potential
component of the energy converts completely to a kinetic one, the velocity of
the cyclist increases until it reaches its maximum value 
at point "D". At this point the total energy is always the same as
points "C" and "B", but it manifests only in the form of
kinetic energy.
After point "D", in the ideal case where no resistive forces act, the
cyclist (if he doesn’t pedal) will continue to move with a constant
velocity forever in accordance with the first Newton’s law. Unfortunately, in
the real case resistive forces exist; if the cyclist doesn’t pedal, after
point "D" he progressively slows down and finally stops.
Imagine a system like the one in the following diagram.
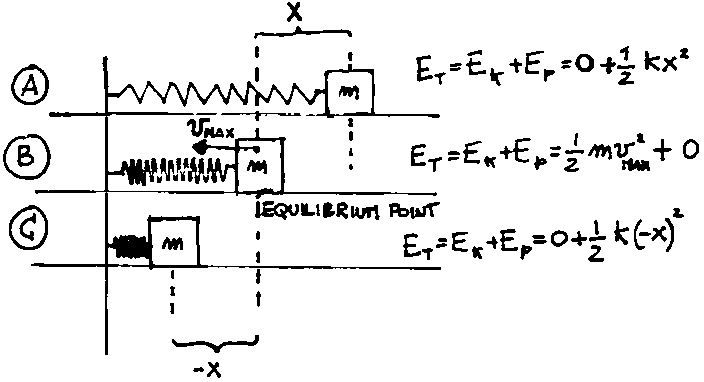
An "m" mass is attached to a spring and the spring is fixed to the
wall. If nobody does work on the spring, the mass rests at the equilibrium
point, the point where the spring is neither stretched nor compressed.
If we pull the mass and stretch the spring to the right of equilibrium point, we
work against the elastic force
of the spring and we increase the potential energy to a value
(such a situation is sketched in figure "A" above).
As usual we suppose the frictional forces negligible. If we release the mass,
the elastic force pulls back and makes the mass move towards the left, the
potential energy converts into kinetic energy and the process goes on until the
equilibrium point is reached. At the equilibrium point "B" the energy
is completely kinetic and the speed has its maximum value. When the mass
overshoots the equilibrium point, the restoring elastic force begins to insist
in the opposite direction because of the compression of the spring; now the
kinetic energy decreases because the mass slows down while the potential energy
increases until it reaches the same starting value. (situation "C").
Then, the process repeats itself and the mass oscillates back and forth while
the total energy passes from the potential to the kinetic form and vice-versa.
If we plot the mass-position versus time graph, we obtain a smooth and harmonic curve called "cosinusoid"
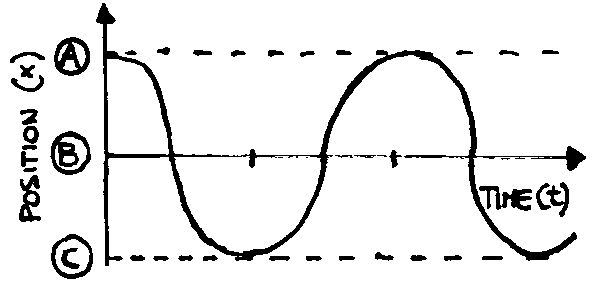
As a matter of fact, any restoring force having a linear dependence on distance (like the elastic one) gives rise to a harmonic motion like the one represented by the curve in the figure.