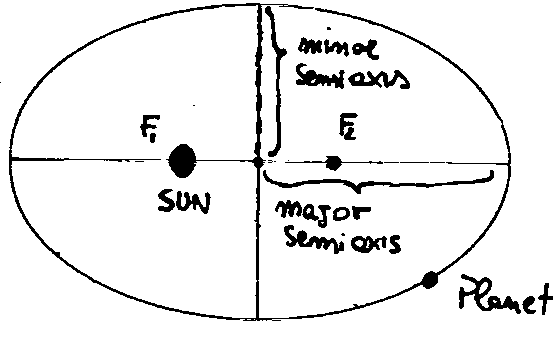
Planets are the most wonderful examples of "bodies" describing a curved trajectory due to a centripetal force.
Looking at the heavenly bodies, the sun, the moon and the stars move across the sky each day and night. Their apparent motion could be explained by picturing them as lying on a giant sphere that revolves around the earth. This geocentric view seems reasonable.
Early models of the motion of the heavenly bodies developed by Greek philosophers involved concentric spheres centered on the earth. The sun, the moon, and the planets had their own sphere. The fixed stars were on the outermost sphere. These spheres revolved around the earth in ways that explained the position of the heavenly bodies.
Ptolemy (Claudio Tolomeo 100-170 A.D.) improved the geocentric model with the introduction of epicycles in order to explain the retrograde motion showed by some planets (see the book on page 81). Ptolemy’s model became part of the accepted knowledge during the Middle Ages and was incorporated, with many of Aristotle’s Work, into the teachings of the Roman Catholic church and the emerging European Universities.
During the sixteenth century, Nicolaus Copernicus (a polish astronomer 1473-1543) developed a revolutionary heliocentric model. Copernicus placed the sun at the centre of the circular orbits of the planets and demoted the earth to the status of the other planets. He introduced the idea that the earth rotates on an axis through its centre thus explaining the daily motion of the sun and the other heavenly bodies. However Copernicus didn’t publish his model until within a year of his death.
Galileo (1564-1642) promoted this model more vigorously than Copernicus himself. Using the telescope he discovered that the moon has mountains, that Jupiter has moons, that Venus goes through phases like our moon. He showed that the phases of Venus could be explained better by the Copernican model than by a geocentric model. Furthermore the Copernican model doesn’t require epicycles to explain retrograde motion: the earth is orbiting the sun with the other planets, so, for instance, because of the fact the earth orbits more rapidly than Mars, when the earth passes Mars, Mars slip behind and briefly appears to move backward. (see the figure 5.13 on page 82 in the textbook).
Johannes Kepler (Keplero 1571-1630) analysed the astronomical data collected by Tycho Brahe (1546-1601) and was able to explain the insubstantialities of the Copernicus model. From Tycho’s data he deduced that the orbits of the planets are not circles but ellipses.
After a hard and patient numerical work on Tycho’s data, he worked out three fundamental laws about the planetary motion:
The planets move in elliptical orbits about the sun with the sun at one focus of the ellipse.
The radius vector connecting the sun to the planet sweeps out equal areas in equal times.
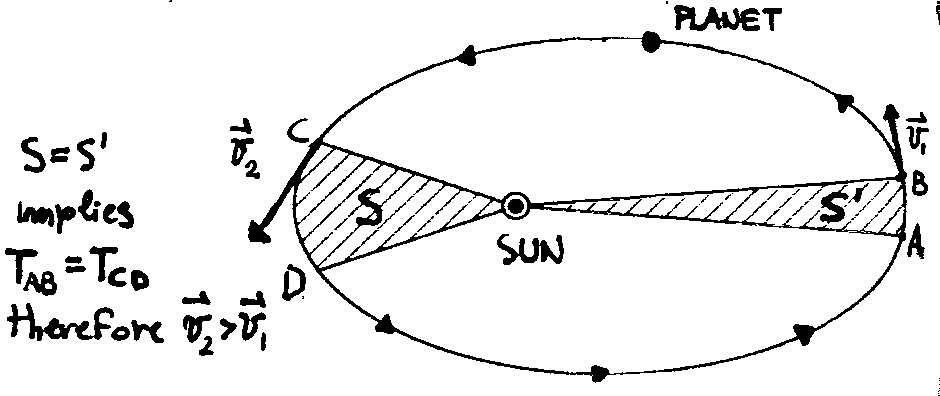
This law means that planets don’t move with a constant speed along the orbit: they move faster when they are near the sun and slower when they are far from the sun. As the planet comes closer to the sun its velocity increase and vice versa.
The square of the period 
(time
required by the planet to cover a whole orbit) is proportional to the cube of
the average distance 
(average
radius) between sun and planet (Note that this distance is equal to the ellipse’s
major semiaxis).
Using Maths, the third law can be expressed in a compact way:
is the
proportionality constant between the two quantities.
depends on the Sun.
The third law can also be stated by saying that the ratio between 
and 
is
constant:
From the physical point of view, the third law states that planets with larger orbits move slower than planets with smaller orbits.
Planetary data applied to Kepler’s Third Law are reproduced in the table below.
Interact with a three dimensional model of the solar system with the java applet at
http://liftoff.msfc.nasa.gov/academy/space/solarsystem/solarsystemjava.html
Observe the planetary motion with the java applet at
http://www.humnet.ucla.edu/humnet/french/faculty/gans/java/SolarApplet.html
Could you recognize the three Kepler’s laws from the last applet?