Percorsi minimi

COS' E' UN PERCORSO MINIMO

Un comportamento medio, che può essere assunto come un dato estremamente significativo nella mobilità generale, è il percorso minimo che ogni individuo cerca di fare per andare da un punto ( origine ) ad un altro ( destinazione ). Il territorio può essere visto come un grafo in cui le città sono i nodi e i percorsi che le collegano sono gli archi.
Dato un nodo origine s e un nodo destinazione t , si vuole determinare il cammino semplice di lunghezza minima che collega s a t.
Il problema del cammino minimo tra due vertici offre evidentemente innumerevoli possibilità di applicazione, sia nel caso di reti di trasporto sia per reti di altra natura (elettriche,idrauliche, di relazione logica tra entità).
Il problema più classico è di determinare il cammino avente costo o tempo minimo tra due nodi assegnati di un grafo.
Infatti lo studio del percorso minimo può essere effettuato utilizzando parametri diversi:

1) OTTIMIZZAZIONE DEL TEMPO
2) OTTIMIZZAZIONE DELLE DISTANZE
3) OTTIMIZZAZIONE DEI COSTI

Se in prima analisi i problemi sembrano non avere correlazione tra loro, in realtà costituiscono lo stesso problema e possono essere studiati con lo stesso metodo, infatti è possibile trasformare l'unità tempo e distanza in unità costo.

GRAFI E CAMMINI

Col termine grafo si definisce un insieme di punti o nodi collegati tra loro da tratti o archi.

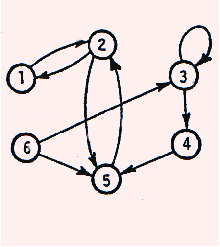
Ogni percorso che parte da un nodo (origine) per arrivare ad un altro (destinazione) si chiama percorso o cammino.
Gli archi di un grafo possono essere orientati in un solo verso (in un senso o nell'altro) o in entrambi i versi.
Spesso agli archi di un grafo sono associati dei valori detti pesi. I pesi possono rappresentare distanze tra i nodi, costi associati al trasferimento da un nodo all'altro, tempi o altro ancora.
A volte anche ai nodi del grafo sono associati dei pesi.

Si veda di seguito un esempio di grafo con la matrice dei pesi ad esso associato.

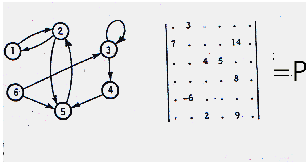
Un problema di percorso consiste nel trovare un cammino tra due o più nodi che minimizzi (o massimizzi) una qualche misura di prestazione, che è funzione (di solito la somma) dei valori degli archi.
Ai cammini ritenuti accettabili si possono imporre un certo numero di vincoli; ad esempio, quello di non ritornare ad un nodo appena attraversato o quello di passare per ogni singolo nodo una sola volta.
Si potranno verificare, inoltre, dei ritardi ai nodi (ad esempio, agli incroci di strade di grande comunicazione o ai tavoli di commutazione di una centrale telefonica).
Tali ritardi possono essere probabilistici dipendendo dal carico di traffico al nodo o dalla disponibilità degli archi che escono dal nodo (strade di grande comunicazione o linee telefoniche).
I collegamenti possono avere capacità limitata (non più di una unità alla volta) o non essere sottoposti a vincoli di capacità.
In alcuni casi, poi, sia i nodi che i collegamenti possono interrompersi o essere chiusi parzialmente o totalmente (ad esempio, per riparazioni).
E' assai comodo (per esempio, al fine di fornire al calcolatore le informazioni) rappresentare un grafo mediante una o più matrici di dimensioni n x n ( se n sono i nodi del grafo): nella posizione (i,j) delle matrici si pongono le informazioni relative all'arco (i,j).
Avremo così la matrice di incidenza, in cui nella posizione (i,j) è posto un 1 se esiste il corrispondente arco e uno 0 in caso contrario, e la matrice dei pesi, contenente ovviamente nella posizione (i,j) il peso associato all'arco corrispondente.
Si dice ciclo un cammino in cui i nodi d'inizio e di fine coincidono.
Un grafo in cui non esistono cicli è detto aciclico (albero in certi casi particolari).
Spesso per avere una matrice dei pesi assegnata in ogni elemento,si assegnano dei pesi fittizi anche agli archi non esistenti.
In questo caso ad un arco (i,j) non fisicamente esistente viene assegnato un valore
w_ij= ¥ (in pratica w_ij = M, con M molto grande).
Quanto agli autoanelli (collegamento tra un nodo e se stesso), il peso loro assegnato dipende dalla possibilità o meno di "stare" nel nodo, cioè di compiere una transizione dal nodo a se stesso.

Si voglia andare da s (origine) a t (destinazione). Vi sono molti percorsi differenti tra s e t, ma si desidera scegliere quello che comporta il minor tempo, costo o distanza.
Nel grafo vanno inseriti dei numeri che rappresentano una qualsiasi di queste misure, la cui somma deve essere minimizzata.
Risulterà che nel ricercare il percorso più breve tra s e t è utile trovare il percorso più breve da s ad ogni altro punto nel grafo.

Procedimento grafico.

Si prenda come esempio il seguente grafo coi relativi costi:

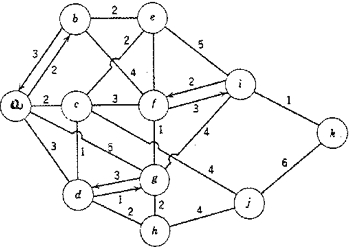
1) Partendo dall'origine, tracciare tutti gli archi con i quali si può andare da
"a " (origine) ad un altro nodo e inserire la distanza diretta da "a" su ognuno di questi nodi.

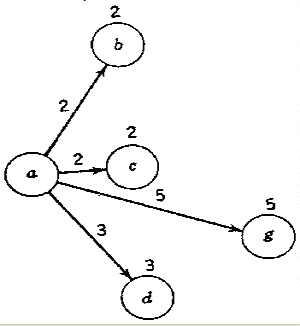
2) Se c' è qualche arco tra i nodi ottenuti nella fase 1, determinare per ogni arco se il percorso indiretto da "a" è più corto di quello diretto.
Si traccia il percorso più breve con una linea continua e il percorso più lungo con una linea tratteggiata. Si scrivono le distanze più brevi a lato di ogni nodo.

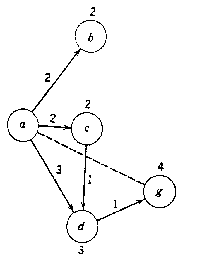
3) Aggiungere tutti i nodi che si possono raggiungere dai nodi considerati nella fase 2 e ripetere la fase 2 rispetto ad essi.

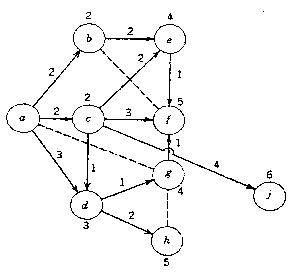
4) Continuare sino alla fine.Nel diagramma completo le linee continue mostrano i percorsi che si possono fare da "a" ad ogni altro punto.

Spesso si preferisce porre un ulteriore vincolo: tra i percorsi di uguale lunghezza deve essere minimizzato il numero dei nodi.

ALGORITMI

Per la risoluzione di problemi di cammini ottimi esistono algoritmi efficienti ed ormai molto diffusi, in grado di affrontare problemi di dimensione anche elevata (1000 nodi ed oltre).
Esistono numerosi metodi di risoluzione per il problema dei percorsi minimi, la maggior parte dei quali è basata sulla programmazione dinamica.
Si descrivono i tre principali algoritmi di risoluzione del problema dei percorsi minimi:
a) ALGORITMO DI BELLMAN - KALABA
b) ALGORITMO DI DIJKSTRA
c) ALGORITMO DI FLOYD - WARSHALL

ALGORITMO DI BELLMAN - KALABA:

Si vuole determinare il cammino minimo tra un nodo origine s (fisso) e gli altri nodi (in un numero qualsiasi di passi).
Si espande il grafo costruendo un grafo aciclico (albero) che ha come nodo di partenza il nodo di origine e come nodi di arrivo tutti gli altri.
Si espande il grafo aciclico per n passi.

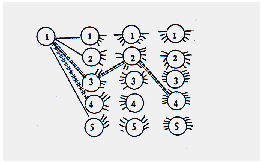
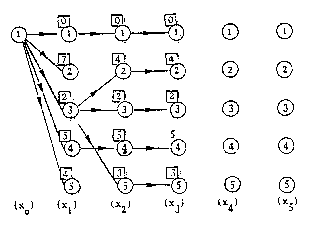
In ciascun passo, a fianco di ogni nodo si pone un' etichetta.
Si definisce etichettatura del passo k l'insieme delle etichette dei nodi di tale passo.
L'algoritmo convergerà sicuramente dopo n passi.
Si noti che, anche se il grafo ha cicli negativi, ha sempre senso il problema se è fissato a priori il numero di passi (cammino di K passi con distanza minima).
Esempio di etichettatura:

ALGORITMO DI DIJKSTRA:

L'algoritmo di Dijkstra richiede che sia soddisfatta la condizione d_ij ³ 0 per ogni arco (i,j) e permette di calcolare il cammino minimo dall' origine s (fissa) ad ogni altro vertice del grafo G.
L' algoritmo di Dijkstra può essere descritto mediante i seguenti passi:
1. si assegna ad ogni nodo i una etichetta l(i) che al termine dell' algoritmo esprime la distanza minima dall' origine s al nodo i. Si pone l(i) = +¥, " i ¹ s, l(s)=0. Si definisce un insieme L di nodi la cui etichetta è resa permanente, ovvero non più modificabile dall' algoritmo. Si pone L=Æ.
2. Tra i nodi i non appartenenti a L, si sceglie un nodo p per cui sia minimo il valore della etichetta, ovvero l(p)=min{l(i):i non appartenenti a L}.
Si rende p permanente L=L È {p}.
3. Si aggiornano le etichette dei nodi i non permanenti raggiungibili da p, ovvero {i.i non appartenente a L, (p,i) appartenente a E }, sulla base della formula l(i) = min{l(i),l(p)+c_pi}
4. Se tutti i nodi hanno etichetta permanente, ovvero se L = V, si arresta l' algoritmo. Le etichette rappresentano le lunghezze dei cammini minimi da s ad ogni altro nodo. Altrimenti si procede al passo 2.

L' operazione fondamentale dell' algoritmo di Dijkstra è costituita dalla formula di aggiornamento delle etichette, nel corso del passo 3:

l(i)=min{l(i),l(p)+cij}

Questa operazione, indicata talvolta con il termine di triangolazione, ha un evidente significato intuitivo: l' etichetta di un nodo l(i) viene aggiornata allorché risulta più conveniente raggiungere i mediante un nuovo percorso, che utilizza il cammino da s a p e successivamente l' arco da p a i. E' possibile dimostrare che, quando un nodo p viene reso permanente, la sua etichetta rappresenta in modo definitivo la lunghezza del cammino minimo da s a p.
Tuttavia, la correttezza dell' operazione di triangolazione, e quindi della formula di aggiornamento delle etichette, viene pregiudicata dalla presenza di archi con distanza negativa.
Si vedano qui di seguito i passi successivi dell' applicazione dell' algoritmo di Dijkstra:

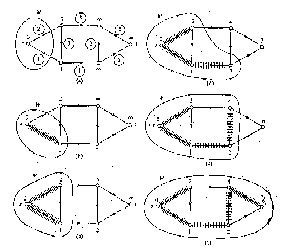
ALGORITMO DI FLOYD - WARSHALL :

Nel caso in cui esistano archi di peso negativo, l'algoritmo di Dijkstra può fornire una soluzione non ottimale.
In tali casi si può tuttavia ricorrere all'algoritmo di Floyd - Warshall, che determina i cammini minimi tra tutte le coppie di nodi del grafo G.
L'algoritmo è corretto sotto l'ipotesi che il grafo G non contenga circuiti a costo totale negativo.
L'algoritmo di Floyd - Warshall si basa sull'applicazione ripetuta dell'operazione di triangolazione.
Viene utilizzata una matrice D di dimensioni n x n, il cui generico elemento dij è destinato a rappresentare, al termine dell'algoritmo ,il costo del cammino minimo da i a j .
1. Si pone d_ij = c_ij se l'arco (i ,j) non appartiene ad E, altrimenti d_ij =+ ¥.
2. Per k =1,2,……n, esegui il passo 3.
3. Per i=1,2…..n, i ¹ k, per j=1,2,…..n, j¹k, si applica la formula di aggiornamento
dij = min{ d_ij , d_ik + d_kj }. Se al termine degli aggiornamenti si ha d_ij< 0 per qualche nodo i, l'algoritmo si arresta poiché esistono circuiti a costo totale negativo.

DIFFERENZE TRA I TRE ALGORITMI

I problemi su grafo hanno un numero finito di soluzioni e quindi si potrebbe esaminarle tutte e poi scegliere la migliore.Ma ciò è praticamente impossibile nella realtà:un problema di percorso ottimo su un grafo con n nodi può essere risolto in n! modi diversi, il che per n=50 vuol dire circa 10⁴⁵ secoli di impiego per un calcolatore capace di esaminare un miliardo di soluzioni al secondo.
E' quindi fondamentale valutare gli algoritmi esaminandone l' efficienza dal punto di vista del tempo di calcolo.
Un algoritmo è preferibile ad un altro se entrambi risolvono la stessa classe di problemi, ma il primo algoritmo ci riesce in un numero di passi inferiore(cioè in tempo più breve).
Il parametro più importante per valutare le prestazioni di un algoritmo è quindi il tempo di esecuzione, misurato contando il numero di operazioni elementari che esso deve compiere nel caso peggiore, cioè in presenza di dati che lo obbligano a compiere tutti i passi che sono stati previsti.
Per questo si parla di complessità computazionale, cioè del numero di operazioni elementari che un algoritmo deve compiere, dato in funzione delle dimensioni del problema. La complessità si esprime in ordine di grandezza o(.) : cosi' una complessità o(n²) indica che l' algoritmo arriva alla soluzione finale con un numero di operazioni proporzionale al quadrato della dimensione n.
Un algoritmo si dice efficiente se la sua complessità è polinomiale, cioè se la funzione o(.) è un polinomio nelle dimensioni del problema.
E' dimostrabile che la complessità computazionale dell' algoritmo di Bellman - Kalaba è una complessità polinomiale = o(n³) , quella dell' algoritmo di Dijkstra è una complessità polinomiale = o(n²) e infine quella dell' algoritmo di Floyd-Warshall e' o(n³).
Nell' algoritmo di Bellman - Kalaba trovare il cammino minimo tra un nodo ed un altro è equivalente a trovare il minimo cammino fra il nodo in questione e tutti gli altri, poiché si procede parallelamente per tutti i nodi.
Ciò non avviene per l' algoritmo di Dijkstra.
E' stato dimostrato che l' algoritmo di Dijkstra è ottimo (cioè ottiene la soluzione ottima per il problema dei cammini minimi).
Nonostante ciò, nell' esempio che seguirà si userà l' algoritmo di Floyd-Warshall in quanto questo permette di calcolare il percorso minimo da un nodo qualsiasi ad un altro nodo, mentre gli altri due algoritmi permettono di determinare il percorso minimo solo tra un nodo fisso (origine s) e gli altri nodi.
L' uso dell'algoritmo di Floyd-Warshall richiederà molta più memoria per il calcolatore perché dovrà mostrare l' intera matrice dei risultati, cioè i percorsi minimi tra tutti i nodi.

Campo di applicazione

Grazie al recente sviluppo dei supporti informatici, lo studio del percorso minimo ha acquisito un' importanza rilevante.
Il problema dei percorsi minimi si presenta nel settore dei trasporti , in quello delle comunicazioni e in molti altri campi, ad esempio nella logistica industriale per la determinazione dell' ordine in cui produrre un insieme di articoli su un impianto di lavorazione comune.
Qui di seguito si analizzano il settore urbanistico e quello dei trasporti.

Settore urbanistico

Un problema molto diffuso è per esempio la collocazione di un dato servizio pubblico (ufficio postale, ospedale, biblioteca…….) all'interno di un settore urbano.
Come è facile intuire, il problema è quello di individuare una o più aree all'interno delle quali collocare tale servizio.
Ovviamente l'ubicazione deve soddisfare uno o più requisiti. Il più importante è il tempo minimo che l'utente generico deve impiegare per raggiungere tale servizio.
Il problema di tempo minimo risulta essere quindi strettamente correlato con il percorso minimo.

Settore trasporti

Altro problema molto diffuso è quello di identificare il percorso dei trasporti pubblici come per esempio pullman, tram, metropolitana ecc…
In questo caso nasce l'esigenza di creare una rete che minimizzi la distanza ottimizzando l'area di copertura del servizio.
La necessità è quindi quella di collegare nella maniera più opportuna i vari punti (fermate, stazioni ecc…) dell'area di utenza.

Gli algoritmi di percorso minimo possono essere utilizzati:
· per determinare il costo minimo (come già detto il costo può essere indifferentemente : "tempo", "distanza" o "costo materiale") tra un nodo ed un altro ed il relativo percorso;

· per determinare l' intera matrice dei costi minimi tra ogni nodo e tutti gli altri,in modo da avere una visione spaziale, che mostri la relazione di ogni "zona" con le altre.

Nel primo caso l' utente può essere un " navigatore" o un "viaggiatore" in generale.
Nel secondo caso tali algoritmi vengono utilizzati per avere una visione d' insieme, ad esempio per costruire una rete elettrica o una rete di trasporti.

Link e riferimenti

Applicazione dell' algoritmo di Dijkstra di Carla Laffra della Pace University:
http://www.dgp.toronto.edu/people/JamesStewart/270/9798s/Laffra/DijkstraApplet.html

Spiegazione e codici in linguaggio c degli algoritmi di Dijkstra e Floyd da parte di Eugenio Moggi (ultima revisione 24 Maggio 1997) :
http://www.disi.unige.it/person/MoggiE/ASD/nota7

Un codice in c++ per l'algoritmo di Floyd costruito da Chi F. Chen il 28/01/01(basato sull'algoritmo tratto dal testo di Thomas H. Cormen, Charles E.Leiserson e Ronald L.Rivest, "Introduction to Alghorithms",MIT & Mcgraw-Hill):
http://www.u.arizona.edu/~chifu/floyd-warshall.html

Applicazione dell'algoritmo di Floyd eseguita da uno studente informatico ( possibilità di vedere come la matrice "cambi" mentre procede l'algoritmo):
http://www.bice.it/Informatica/Algoritmi/Floyd/Floyd.html

Calcolo di distanze minime tra città:
http://www.kwmappe.kataweb.it/itinerari.htm

http://www.viamichelin.com/viamichelin/ita/dyn/controller/mapHomePage

http://mappe.virgilio.it/mappe/index.html

Per un approfondimento teorico sugli argomenti qui trattati si possono vedere:

Carlo Vercellis , "MODELLI E DECISIONI:STRUMENTI E METODI PER LE DECISIONI AZIENDALI", Progetto Leonardo , Bologna (1997).

Niklaus Wirth, " ALGORITMI + STRUTTURE DATI =PROGRAMMI", Tecniche Nuove, Milano (1987) - (Trad. di Stefano Piccardi).

Christos H. Papadimitriou , Kenneth Steiglitz, "COMBINATORIAL OPTIMIZATION: Alghorithms and complexity" , Englewood Cliffs , Prentice Hall (1982).

Alberto Colorni , " RICERCA OPERATIVA" , Clup, Milano (1988).

Russel L. Ackoff, Maurice W.Sasieni , "LA RICERCA OPERATIVA : PRINCIPI, METODI, TECNICHE" , ETAS LIBRI, Milano (1977) - (Trad. di Luisa Regalia - Titolo originale: "Fundamentals of operations research" )