Frattali

La ripartizione della popolazione nello spazio è una questione fondamentale in tutte le riflessioni sui meccanismi sociali ed economici di un territorio.

Numerose discipline hanno dunque cercato di studiare questo fenomeno in contesti e scale differenti: demografi, geografi, ma anche urbanisti ed economisti.

Qualsivoglia sia la scala di osservazione, i risultati ottenuti mostrano che le attività umane non sono ripartite in modo omogeneo nello spazio. Le ragioni paiono molteplici: da una parte esistono condizioni più o meno favorevoli allo sviluppo di tali attività, per lo meno per quelle che influenzano la dislocazione degli abitati, dall’altra lo stato di fatto urbano ha provocato la gerarchizzazione delle città.

Tutto ciò è stato da sempre oggetto di tentativi di formalizzazione da parte di studiosi e tecnici.

Se l’esistenza di una ripartizione eterogenea sembra onnipresente nelle analisi teoriche del funzionamento dei sistemi di distribuzione della popolazione, si può constatare che le misure utilizzate siano tutte basate su paradigmi di spazi uniformi; il riferimento geometrico rimane l’omogeneità. In effetti la misura più utilizzata è la densità, la quale indica una occupazione media del territorio, supponendo una proporzionalità tra popolazione e superficie occupata. I risultati da tempo noti mettono in evidenza l’ambiguità di quest’approccio.

Dal momento che gli urbanisti non possono più far riferimento alla città circolare o lineare, caratterizzano il tessuto urbano contemporaneo come amorfo e irregolare, senza nessuna organizzazione interna apparente.

Studi più approfonditi di alcuni fenomeni complessi, non lineari, hanno mostrato l’insufficienza di questi concetti tradizionali. Potremmo citare come esempi la scoperta degli attrattori caotici e dei fenomeni legati alle transizioni di fase.

Come unico approccio alternativo di carattere puramente geometrico, si è affermato fin ora solo la geometria frattale.

Tale approccio si basa su una logica binaria che distingue il territorio in urbanizzato e non urbanizzato. E’ necessario fare un’introduzione a quella che è la geometria frattale.

LA GEOMETRIA FRATTALE

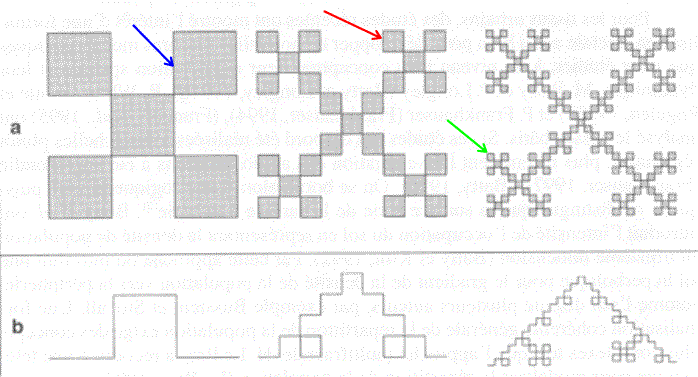
Per ottenere un frattale (Fig.1) è necessario scegliere una figura iniziale,nel nostro caso un quadrato di lato L e, successivamente deve essere scelta un’operazione geometrica che trasformi la figura iniziale, denominata generatore.

Nel nostro esempio la figura iniziale è ridotta per un fattore r = 1/3, venendo a creare così N = 5 quadrati (freccia blu) simili a quello iniziale, ciascuno di lato l₁= r * L = 1/3L.

^{_{Quest’operazione è poi ripetuta per ciascuno dei 5 quadrati formatisi. La
figura che otteniamo è formata da N₂ = N²= 25 quadrati (freccia rossa), ognuno di lato l₂ = r² *
L = 1/9L.
Nel passaggio successivo si sono venuti a formare 125 quadratini (freccia
verde), e si può osservare che l’aspetto a scacchiera è scomparso, lasciando il
posto ad una gerarchia spaziale che si manifesta tramite una successione di
spazi occupati e spazi liberi, anche detti lacune.
Proseguendo quest’applicazione iterativa per n volte, otterremo:
_{^{N_n = Nⁿ
quadrati
_{^{ln = rⁿ * L
lunghezza di ogni lato
a_n = l_n²
area di ogni quadrato
Calcolando l’area e il perimetro totale della figura ottenuta possiamo ottenere
questi risultati:
A_n = N_n * a_n = (N * r²)ⁿ *
L² = (5/9)ⁿ * L²
P_n = N_n * 4 * l_n = (N * r)ⁿ * 4 *
L = (5/3)ⁿ * 4 * L
Osservando i numeri tra parentesi (5/9<1;5/3>1) è immediato constatare
che se il numero n di iterazioni fosse infinito otterremmo un’area totale
nulla e un perimetro complessivo infinito.
Questo comportamento è contro intuitivo, ed il fatto che la lunghezza di una
curva cresca all’infinito sembra indicare che essa abbia una dimensione
maggiore di uno, nonostante essa rimanga topologicamente lineare. Tutto ciò non
è più in concordanza con la geometria tradizionale, vengono introdotte delle
dimensioni frazionarie (Fig.5).



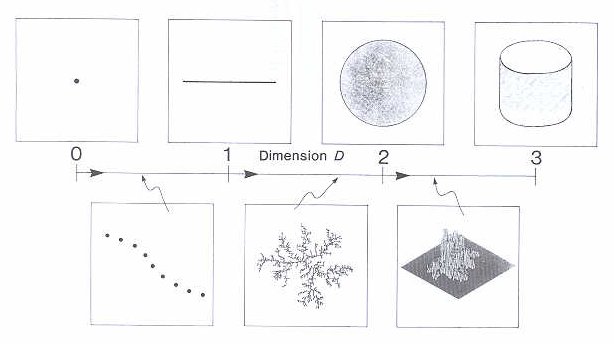
Anche la misura di tale dimensione non verrà ricavata in modo tradizionale,
ma tramite la seguente relazione:
D_s = log N / log (1/r)
e nel nostro caso specifico otterremmo:
D_s = 1.47
Questo valore vale per la figura nella sua totalità, comprendendo area e
perimetro, discordando vistosamente con la geometria tradizionale, nella quale
la dimensione di una curva è uno e quella di una superficie è due.
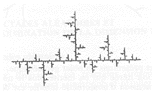
E' possibile ricorrere al metodo dell’applicazione iterata per introdurre un
altro tipo di frattale, il frattale ramificato (Fig.2).
Esso è caratterizzato da una topologia lineare, ma mostra delle gerarchie
interne comparabili a quelle del tappeto di Sierpinski. Nell'esempio considerato
sia
la figura iniziale che il generatore formano una croce greca(N
= 5 ; r = 1/3).
E’ possibile osservare delle linee a lunghezza decrescente:
2        sezioni di lunghezza L
(freccia blu)
5⁰ * 4 sezioni di lunghezza r * L
(freccia
rossa)
5¹ * 4 sezioni di lunghezza r² * L
(freccia
verde)
5² * 4 sezioni di lunghezza r³ * L
(non rappresentato)
_^{^….}
E, dopo n iterazioni:
5^n-1 * 4 sezioni di lunghezza rⁿ * L.



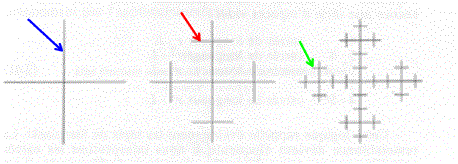
Fino ad ora sono stati considerati solamente frattali generati da un solo
fattore di riduzione. Questo tipo di figure vengono chiamate monofrattali.
Si possono costruire delle gerarchie più complesse se il generatore è
costituito da più fattori di riduzione. Si potrebbero infatti produrre N₁
elementi di taglio r₁ * L e N₂ elementi di taglio r₂ * L.
Una tale struttura si inscrive in una logica multifrattale
(Fig.3-Fig.4).



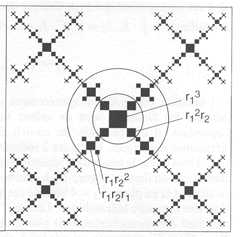
Il fattore di riduzione può anche essere combinazione di multipli dei due
fattori iniziali (r = r₁^a * r₂^b).
Tramite le strutture multifrattali si può osservare che si generano differenti
areole di quadrati della stessa grandezza, ma con “importanza” differente:
gli elementi periferici della prima areola hanno la stessa grandezza degli
elementi della seconda, ovvero si trovano elementi dello stesso taglio in differenti
tipi di aggregati.



I METODI DI ANALISI FRATTALE

Sono stati elaborati metodi di misura che si collocano in una logica
equivalente a quella dell’iterazione: si introducono una sequenza di misure di
taglio variabile e e, per ogni valore e,
si determina il numero di elementi N(e)
necessari per ricoprire la struttura.
Sono stati sviluppati molti metodi per trasferire questa logica in algoritmi
concreti, permettendo di analizzare il comportamento frattale delle strutture.
In particolare, per quel che riguarda l’analisi dei sistemi urbani, sono stati
utilizzati in particolare quattro metodi: l’analisi a griglia, l’analisi
della dilatazione e l’analisi della correlazione per quanto riguarda
informazioni generali sulla ripartizione spaziale (analisi globali); l’analisi
radiale per informazioni più dettagliate (analisi locali).

Analisi a griglia:
Si ricopre con una griglia la zona da studiare e si fa variare il taglio e
delle maglie; dopodiché per ogni valore e si
contano il numero N(e) di maglie che
contengono dei punti occupati.
Tramite la seguente relazione logaritmica è possibile calcolare la
dimensione della griglia D_q_:}}
log N(e) = log (cost) - D_q * log (e)
E’ evidente l’ambiguità del risultato ottenuto, in quanto esso dipende
dal taglio della maglia e dalla zona (finestra di analisi) scelta per applicare
la griglia. Questo problema si presenta in particolare quando stiamo trattando
delle figure multifrattali.

Analisi della dilatazione:
Si circonda ogni punto occupato da un quadrato di taglio e
e si considera l’interno di questo quadrato-test come superficie occupata.
Gradualmente viene ingrandito il taglio e determinata la superficie totale
annerita ad ogni iterazione A(e).
Progressivamente si perdono i dettagli dei tagli inferiori a e
e si ottiene un’approssimazione della figura originaria. Dividendo quest’area
per l’area del quadrato-test si ottiene il numero di elementi sufficienti per
coprire l’intera figura.
A(e) / e²
= N(e)
Si ottiene una relazione analoga alla precedente, in cui però la dimensione
è D_m:
log N(e) = log (cost) - D_m * log (e)

Analisi della correlazione:
A partire da ogni punto della figura, si conta il numero di punti occupati
situati ad una certa distanza da quello preso come punto di riferimento, ovvero
il numero delle correlazioni. Si arriva alla stessa formula bilogaritmica in cui
la dimensione è D_c. L’informazione che fornisce questo metodo è più
dettagliata rispetto a quella fornita dall’analisi a griglia.

Analisi radiale:
Essa si riferisce ad un punto preciso, scelto come centro del conteggio. La
maglia e è sostituita da un cerchio di raggio
r, all’interno del quale è necessario
contare il numero di punti occupati N(r).
La relazione che si ottiene è la seguente:
log N(r) = D_r * log (r)
Essa permette di esplorare la microstruttura di un tessuto urbano.
Comportamento di scala:
La distorsione logaritmica può essere di disturbo se volessimo mettere in
evidenza i cambiamenti del comportamento frattale all’interno di una figura.
Per evitare questo si calcola il valore locale della pendenza, funzione della
distanza progressiva r_i.
a_i = (log (N_i) - log (N_i-1)) / (log (r_i) -
log (r_i-1))
Questa è la relazione del comportamento di scala.
Per tutte le città è possibile osservare una ripartizione frattale della
superficie edificata. I risultati ottenuti da numerosi ricercatori sono
concordanti e le dimensioni trovate variano tutte tra 1.31 e 1.99. Anche se una
comparazione diretta sembra difficile, vista l’influenza dei differenti modi
di rappresentazione cartografica, il fatto di osservare un comportamento
frattale in tutti i casi dimostra l’esistenza generale di un tipo di
organizzazione spaziale.
Per illustrare le caratteristiche generali dei metodi di analisi, sono di
seguito rappresentate le curve che si ottengono per la città di Mosca (Fig.6).



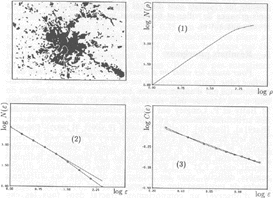
Risulta molto interessante investigare il modo in cui cambia la dimensione
frattale passando dal nucleo urbano più interno fino alle zone periferiche
(Fig.7).




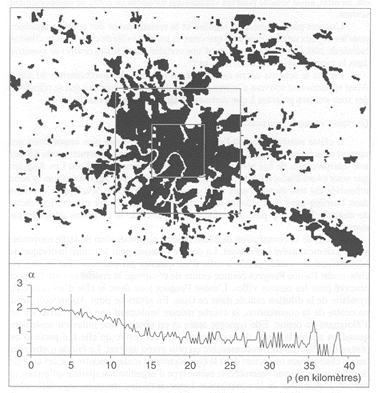
Allontanandosi dal centro del riquadro più interno, il comportamento di scala resta abbastanza
costante, con un indice a di valore molto elevato che si colloca intorno a 1.8. Queste zone
corrispondono ai nuclei urbani.
Quando si supera il limite di queste zone centrali e si entra nel riquadro
esterno, il valore di a
diminuisce. Questa discontinuità indica un cambiamento nell’organizzazione
spaziale. La zona in questione è considerata a densa urbanizzazione.
All'esterno del riquadro grande si può osservare una fascia molto ampia che corrisponde alla corona periferica della
zona urbanizzata. La curva corrispondente diviene sorprendentemente regolare ed il valore
dell’indice a è decisamente più basso.
All’esterno della corona periferica compare una nuova zona di transizione, dove l’indice
diminuisce ulteriormente.
Visualizzando contemporaneamente l'andamento dell'indice a
e la densità di urbanizzazione che traspare dalla figura è possibile notare
l'esatta corrispondenza della posizione dei riquadri nel disegno e delle
fratture nelle curve. Questo significa che l'analisi del comportamento di scala
spiega molto bene la distribuzione delle zone urbanizzate di Mosca.
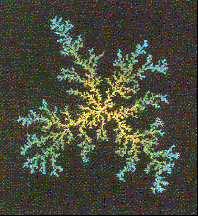
Esistono dei modelli chiamati Diffusion-Limited Aggregation (DLA) Models, i quali
sono in grado di sviluppare le figure frattali necessarie per le analisi appena
citate (Fig.8).


Campo di applicazione
APPLICAZIONI GENERALI
Il campo applicativo delle figure frattali è molto vasto, esse infatti si
prestano tanto bene ad utilizzi puramente grafici, generando figure molto
suggestive (Fig.9), quanto ad ogni processo di diffusione spaziale, essendo
basati su concetti matematici piuttosto complessi e facilmente adattabili a
problematiche diverse.



Si definisce come diffusione spaziale il fenomeno di propagazione nel tempo e
nello spazio di un elemento semplice o complesso. Un virus in seno ad una
popolazione, dei turisti sul litorale della Costa Azzurra, il raffreddamento di
un solido in inverno sono tutti esempi di processi diffusivi. Questa definizione
corrisponde a prendere simultaneamente in conto lo spazio (il frattale si
sviluppa occupando lo spazio) ed il tempo (il frattale è costruito tramite
successive iterazioni) (Fig.10). Inoltre, essa rivela che tutte le strutture
spaziali, per esempio quella di una città, non sono altro che uno stato del
processo di diffusione in una certa data fissata.


APPLICAZIONE AI SISTEMI URBANI

Su scala locale l’analisi frattale si presenta come un potente mezzo per
studiare l’organizzazione spaziale dei tessuti urbani. Essa può mettere in
evidenza l’esistenza di una gerarchia spaziale all’interno di un agglomerato
che in prima analisi non mostra nessun tipo di razionalità nel modo in cui è
stato concepito. Inoltre essa può evidenziare anche la ripartizione non
omogenea delle attività umane nello spazio e i cambiamenti nell’organizzazione
spaziale dei tessuti stessi.
Su scala regionale, essendo questi studi realizzati a partire da piccole scale
che trascurano i dettagli intra-urbani, l’analisi frattale è utilizzata per
ottenere informazioni globali sull’organizzazione spaziale delle città. Per
quel che riguarda grandi città circondate da città “satellite” più
modeste, si sono potuti verificare risultati molto simili a quelli che si
otterrebbero relazionando un nucleo urbano con la sua periferia.
L’analisi spaziale dei processi di urbanizzazione è fondamentale per
comprendere la dinamica dell’evoluzione di una città. Attraverso un’analisi
frattale è possibile mettere in evidenza le tappe successive dell’urbanizzazione,
paragonando i tessuti di una città in diverse date. Spesso la crescita di una
città non è il frutto di una politica di gestione precisa, quindi è possibile
parlare di una sorta di fenomeno di auto-organizzazione (Fig.11).



Attraverso i frattali è possibile schematizzare la struttura dei sistemi di
trasporto. Questa possibilità è direttamente legata alle caratteristiche
geometriche intrinseche di tali sistemi: sono ramificati, presentano diffusione
della lunghezza del percorso. Ovviamente il tipo di frattali più adatto a
descriverli è quello dei cosiddetti frattali ramificati, senza però
dimenticare che anche il perimetro dei frattali comuni può essere utile allo
scopo. E’ fondamentale aggiungere che la geometria frattale per sua natura è
conforme alla necessità di ottimizzazione di una linea di sistemi di trasporto.
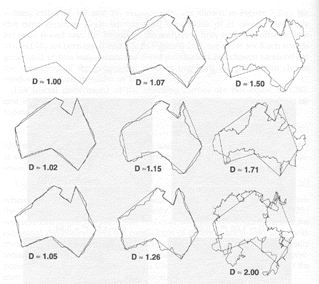
Il perimetro di una figura frattale può essere utilizzato per compiere delle
misure. Il problema è divenuto celebre come “coastline-of Britain-analysis”,
ed è servito a mettere in luce una proprietà curiosa delle frontiere. La
lunghezza delle frontiere varia in funzione della scala scelta: una
rappresentazione cartografica dettagliata, per esempio, mostra una lunghezza
maggiore di una rappresentazione più grossolana, in quanto rappresenta anche
piccole insenature o curvature che contribuiscono a formare il perimetro
(fig.13).


Expertise
Ad oggi non vi sono software o applicazioni pratiche disponibili.

Link e riferimenti
Per un approfondimento teorico sulla geometria frattale :

Feder J., Fractals, Plenum Press, 1988.
Falconer K.J., Fractal Geometry: mathematical foundations and applications,
Wiley, 1990.
Gouyet J.F., Physique et Structures Fractales, Masson, 1992.
Per un’analisi più approfondita delle applicazioni urbanistiche mostrate
in questa pagina :
Batty M., Longley P., Fractal Cities, a Geometry of Form and Function,
Academic Press, 1994.
Frankhauser P., La Fractalitè des Structures Urbaines, Anthropos,
1994.
Frankhauser P., L’Approche Fractal, un nouvel outil de rèflexion dans l’analyse
spatiale des agglomèrations urbaines, Congressi e Colloqui, 1997.

Per un’analisi delle applicazioni fisiche e geografiche:

Douphinè A., Chaos, Fractales et Dynamiques en Gèographie, Reclus,
1995
Non sono disponibili in rete riferimenti specifici all'applicazione
delle figure frattali in campo urbanistico, per quel che riguarda le figure
frattali in senso puramente grafico è possibile visitare questo sito, cliccando la
sezione "frattali", appunto.
http://sprott.physics.wisc.edu}}}}