Clustering

 Descrizione del metodo

 Campo di applicazione

 Expertise

 Link e riferimenti

 Esempi

 Descrizione del metodo

 I termini di Cluster Analysis e classificazione vengono usati indistintamente per descrivere quelle tecniche che cercano di raggruppare variabili o oggetti in determinate classi o gruppi. In particolare le tecniche possono essere usate per ottenere una diminuzione del numero di dati, riducendo le informazioni di N individui in g gruppi al fine di ottenere una riduzione della dimensione dei dati da analizzare, garantendo però la minima perdita di informazioni. Il procedimento secondo cui decidere in quale gruppo un nuovo individuo deve essere allocato viene definito allocazione o assegnazione.

Il risultato di una cluster analysis, quindi, è il numero di gruppi, detti “cluster”, e la loro relativa composizione.

Le strategie di Clustering sono così classificate:

• Tecniche gerarchiche, nelle quali le stesse classi sono distinte in gruppi, il procedimento viene ripetuto a livelli differenti fino a costruire un albero;
• Tecniche di partizione, nelle quali i cluster vengono creati ottimizzando un certo criterio;
• Tecniche di ricerca di densità, nelle quali i cluster sono individuati ricercando le regioni che contengono una fitta concentrazione di entità;
• Tecniche di collegamento, nelle quali le classi o i blocchi possono essere sovrapposti.

Prima di procedere alla classificazione si può scegliere se operare una normalizzazione degli elementi di partenza.

Essa viene generalmente eseguita quando si riscontra una disomogeneità nelle unità di misura dei diversi parametri caratterizzanti il campione di dati (ad es. il reddito misurato in £ e la densità misurata in n° abitanti/ m²).

Adimensionalizzando i dati di partenza, tale operazione permette di creare una certa omogeneità dei dati su cui effettuare l’analisi.

Sulla base dell’obbiettivo che l’operatore intende conseguire, i dati possono essere normalizzati rispetto al loro valor medio oppure rispetto ad un valore massimo (o minimo) stabilito a priori da chi effettua l’analisi .

Dato un certo numero di dati e dopo aver stabilito il valore rispetto al quale effettuare la normalizzazione, tale operazione consiste nel dividere ciascun dato per il valore di riferimento scelto.

dove

• X = dato di partenza

• X_R = valore di riferimento rispetto a cui si vuole operare la normalizzazione

• s = dato normalizzato

I dati così ottenuti sono più omogenei e facili da gestire. Qualora, però, i dati abbiano un diverso peso, l’operazione di normalizzazione ha di contro la perdita di informazione relativa ad esso.

Un caso particolare di normalizzazione è la standardizzazione.

Dato un certo campione di dati e dopo averne calcolato media e scarto quadratico medio, tale operazione consiste nel sottrarre a ciascun dato il valore dello scarto quadratico medio e nel dividere il valore così ottenuto per il valore della media determinato.

dove

• X = dato di partenza
• X_m = valore medio dei dati di partenza
• s = scarto quadratico medio dei dati di partenza
• s = dato standardizzato

Tale operazione permette la realizzazione di un campione di dati caratterizzato da :

• un valore della media pari a 0;
• un valore di scarto quadratico medio pari a 1.

Le tecniche di cluster analisys conducono a differenti risultati a seconda che l’insieme iniziale dei dati sia stato normalizzato ( o standardizzato) oppure sia stato introdotto nell’analisi senza alcun trattamento preliminare.

Numerose tecniche di clustering comportano il calcolo di una matrice delle similarità (o delle distanze) tra gli elementi.

Due modalità di valutazione della distanza sono:

• Metrica Modulo

• Metrica Modulo

Tecniche gerarchiche

Vengono suddivise in:

• metodi agglomerativi che riducono i dati in un singolo gruppo;
• metodi divisivi che separano l’intera serie di dati in N gruppi, ciascuno contenente una singola entità.

I metodi agglomerativi partono dal calcolo di una matrice delle distanze tra gli elementi (solitamente si utilizza la distanza Euclidea) e ad ogni stadio dell’analisi fondono i gruppi o le entità simili (o vicini) tra loro. La distanza viene definita in modo diverso per ogni metodo come vedremo successivamente in dettaglio.

Tra le tecniche gerarchiche agglomerative consideriamo:

• la centroid cluster analysis;
• il Ward's method;
• il single link method.

Nel centroid cluster analysis i gruppi vengono descritti nello spazio euclideo e posizionati attraverso le coordinate del loro centroide. La distanza tra gruppi è definita come la distanza  tra i loro centroidi e prima vengono raggruppati i gruppi con la distanza più piccola .

Nel Ward’s method, Ward propone la teoria secondo la quale ad ogni stadio dell’analisi la perdita di informazioni che deriva dal raggruppamento di elementi può essere misurata dalla somma delle deviazioni quadratiche di tutti i punti. Ad ogni passo dell’analisi viene considerata l’unione di tutte le possibili coppie di cluster e vengono combinati tra loro i due cluster il cui raggruppamento fornisce il minimo aumento di errore nella somma dei quadrati.

Le tecniche gerarchiche basate sull’utilizzo del legame singolo consentono di raggruppare gli elementi tramite una serie di collegamenti intermedi, ma non permettono di modificare il criterio iniziale di raggruppamento, impedendo in tal modo lo spostamento di oggetti tra i singoli gruppi. Mediante questo metodo vengono fusi i gruppi caratterizzati da una distanza relativa tra di essi minima. Nella fase iniziale dell’analisi ciascun gruppo è costituito da un singolo elemento. Il legame singolo è l’unico metodo in grado di soddisfare i concetti di continuità e minima distorsione tra gli elementi. Nell’applicazione di esso l’utente può trovarsi ad affrontare il problema dei vincoli.

I metodi divisivi si distinguono in:

• monotetici, che si basano sulla valutazione di uno specifico attributo;
• polittici, che invece considerano il valore assunto da tutti gli attributi.

Il risultato di queste due tecniche può essere presentato sotto forma di dendogramma a due dimensioni che illustra le partizioni fatte ad ogni passo successivo, si cerca così il passo più efficiente nella progressiva suddivisione (o sintesi) della popolazione.

L’utente può decidere a quale livello o ciclo d’iterazione dell’analisi fermarsi.

Esempio di applicazione di tecnica gerarchica

Si illustra di seguito il funzionamento di una tecnica di aggregazione gerarchica , evidenziandone i caratteri salienti .

Consideriamo la seguente tabella relativa al livello di alfabetizzazione della popolazione dei principali comuni (per numero di abitanti) della provincia di Sondrio:

Applicazione relativa alle tecniche gerarchiche

Si illustra di seguito il funzionamento di una tecnica di aggregazione gerarchica , evidenziandone i caratteri salienti .

Consideriamo la seguente tabella relativa al livello di alfabetizzazione della popolazione dei principali comuni (per numero di abitanti) della provincia di Sondrio:

Censimento Istat 1991

 

Per sviluppare il modello del Clustering si possono utilizzare tre differenti metriche :

• Euclidea
• Modulo (o Manhattan)
• Euclidea e Modulo alternate

Metrica Euclidea

Definiti due generici elementi i e j (ad esempio Chiavenna e Morbegno) , ognuno dei quali è caratterizzato da k parametri (nel nostro caso i sei gradi di alfabetizzazione),si costruisce una matrice delle distanze i cui elementi d_ij sono ottenibili da:

d_ij = S(X_ik -X_jk)²

Quindi la distanza tra Chiavenna e Morbegno, d₁₂ , risulta 

d₁₂ =(241-163)² + (1070-772)² + (1894-1253)² +…+ (9-7)² = 733617

Conseguentemente si ottiene la matrice delle distanze:

Il primo passaggio del procedimento consiste nella fusione dei due elementi che sono più vicini, individuati ricercando nella matrice la distanza minore.

Nel caso in esame si trova che tale distanza è 136355, valore che unisce il primo e il quinto elemento, Chiavenna e Tirano. Avendo valori prossimi, i due comuni costituiscono un' unica entità; pertanto mantenere le informazioni relative ad entrambi non è più significativo.

Se si considera Chiavenna "inserita" in Tirano, si possono eliminare la prima riga e la prima colonna ridefinendo le distanze dei rimanenti elementi rispetto alla coppia. Ne risulta la seguente matrice:

La più piccola distanza risulta essere 279732 (Morbegno e Tirano); procedendo come sopra si ottiene:

In questo caso il valore più piccolo è la distanza 423284, relativa ai comuni di Teglio e Tirano. Si eliminano la seconda riga e la seconda colonna.La matrice finale che si ottiene è:

L'ultimo passaggio consiste nella fusione dei due gruppi rimanenti (Sondrio e Tirano), dando luogo ad una singola entità che contiene tutti e cinque gli elementi.

Metrica Modulo

Definiti due generici elementi i e j (ad esempio Chiavenna e Morbegno) , ognuno dei quali è caratterizzato da k parametri (nel nostro caso i sei gradi di alfabetizzazione),si costruisce una matrice delle distanze i cui elementi d_ij sono ottenibili da:

d_ij = S abs ( X_ik -X_jk )

Quindi la distanza tra Chiavenna e Morbegno, d₁₂ , risulta :

d₁₂ =|241-163| + |1070-772|+ |1894-1253|+…+ |9-7|= 1601

Conseguentemente si ottiene la matrice delle distanze:

Il valore minore è 719 (Chiavenna e Tirano), si considera Chiavenna inserita in Tirano e si eliminano la prima riga e la prima colonna in maniera tale da ottenere:

Proseguendo si raggruppano i comuni di Morbegno e Tirano:

La distanza più piccola è 1611 (Teglio e Tirano); si eliminano la seconda riga e la seconda colonna e si fondono i comuni rimanenti (Sondrio e Tirano).

Metrica Euclidea e Modulo alternate

Il primo passaggio consiste nel ricercare il minimo valore nella matrice delle distanze espressa in metrica euclidea. Nel caso presentato risulteranno uniti Chiavenna e Tirano.

Semplificata la prima matrice, il secondo passaggio consiste nell'operare secondo la metrica assoluta. Si opererà sulla matrice:

Ne deriva il legame tra Morbegno e Tirano. Poiché i due metodi si alternano si considera la matrice euclidea 3x3:

La distanza più piccola è relativa ai comuni di Teglio e Tirano, si riuniscono i due elementi rimanenti (Sondrio e Tirano).

Il risultato finale del processo è un grafico che prende nome di dendogramma.

Nell'esempio qui considerato l'ordine dei raggruppamenti è il medesimo, conseguentemente il grafico seguente visualizza i risultati di tutti e tre i procedimenti.

Se gli oggetti che studiano sono più numerosi si può considerare anche la presenza di vincoli. I vincoli sono della stessa natura dei parametri e la loro individuazione permette di costruire una matrice che evidenzia gli elementi già collegati tra di loro e che ha l'effetto di rafforzare i legami definiti nella matrice delle distanze.

Tecniche di partizione

Sono tecniche che dividono la serie iniziale di dati ottimizzando alcuni criteri predefiniti e, ammettendo una rilocalizzazione delle entità, consentono ad una partizione iniziale non efficiente di essere corretta ad uno stadio successivo.

Il numero di gruppi da analizzare può essere deciso a priori dall’utente ed eventualmente può essere cambiato durante il corso dell’analisi.

Le fasi da eseguire sequenzialmente, sono:

1. Inizializzazione dei cluster;
2. Allocazione delle entità nei cluster;
3. Riallocazione di alcune o tutte le entità in altri cluster al termine del processo iniziale di classificazione

Nella fase di inizializzazione il ricercatore è interessato a dividere la serie di dati in un preciso numero di cluster detto k. I k punti trovati nello spazio bi o tri-dimensionale vengono usati come stima iniziale del centro del cluster. In seguito gli elementi vengono allocati nei cluster al cui centro sono più vicini. La stima del centro di ciascun cluster può essere aggiornata dopo l’addizione di ciascun oggetto al gruppo o dopo che tutti gli elementi sono stati allocati.

La riallocazione è, invece, un’operazione che viene eseguita su quelle entità che devono essere riassegnate in un altro cluster, con l’obbiettivo di ottimizzare il criterio di partizione utilizzato.

La procedura di riallocazione viene ripercorsa finché lo spostamento di una variabile comporta un miglioramento.

Tecniche di ricerca di densità

Se le entità sono rappresentate come punti in uno spazio metrico, il clustering suggerisce che le parti in cui la densità di punti è maggiore siano separate da zone a bassa densità.

Le tecniche classiche tendono ad incorporare le entità in un gruppo già esistente piuttosto che creare uno nuovo.

Un metodo di classificazione è AMOEBA . Proposto per serie di dati spaziali, riesce a trovare tutti i possibili gruppi nelle serie di dati. Esso non richiede parametri all’utente e genera un cluster multi-livello. La visualizzazione dei risultati si ha su un pendrogramma.

In fig. 1 si riporta un esempio in cui si vede identificato il gruppo A come la principale area urbana; questa viene suddiviso in due cluster (AA e AB) al livello successivo e tutti i possibili cluster sono riportati sul pendrogamma.

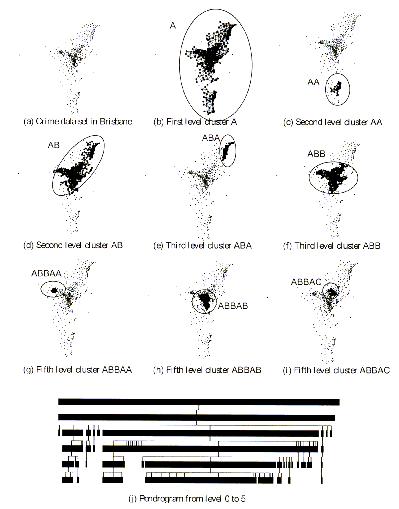
fig. 1

Tecniche di collegamento

Queste tecniche consentono sia una sovrapposizione sia una distinzione dei cluster in base alle richieste dei diversi campi di applicazione.

Calcolando dapprima la matrice delle similarità dai dati originali, queste tecniche permettono di stimare la similarità tra ciascuna coppia di elementi in base alle loro proprietà. Alla fine del processo gli oggetti si ritrovano suddivisi in due soli gruppi, il più piccolo dei quali rappresenta la classe cercata. Le partizioni sono trovate minimizzando una funzione di coesione tra i due gruppi che deve essere resa minima tramite successivi spostamenti degli oggetti.

Un’espressione proposta per la funzione di coesione è la seguente

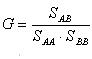
dove

• A e B si riferiscono a due gruppi nei quali i dati sono ripartiti
• S_xy è la somma di similarità tra i membri di x e i membri di y; essa è definita come :

dove

• S_ij è un coefficiente di similarità tra l’elemento i-esimo del gruppo x e l’elemento j-esimo del gruppo y.

 Campo di applicazione

 La Cluster Analysis è una tecnica di analisi statistica che individua una serie di operazioni mediante le quali è possibile collegare gli elementi di un insieme ampio di dati. Prima di procedere al raggruppamento occorre definire un opportuno criterio di valutazione e di selezione e quindi di aggregazione degli oggetti del campione in esame.

La Cluster Analysis presenta due fasi di lavoro:

• definizione dei dati da esaminare e dei loro parametri;
• individuazione di una matrice delle distanze, o delle similarità, relativa agli oggetti in esame, dove si individuano gli elementi più simili tra loro da raggruppare.

Le operazioni di collegamento tra gli oggetti dell’insieme di dati vengono visualizzate attraverso un grafico ad albero chiamato dendogramma. Esso è un grafico, strutturato per livelli, ad ogni nodo del quale corrisponde un cluster.

Grazie ad esso è possibile visualizzare il risultato del processo iterativo che si è compiuto sull’insieme dei dati.

La lettura del dendogramma varia a seconda della tipologia di tecnica di classificazione adottata per l’analisi:

• in un processo agglomerativo, ogni elemento è visualizzato come un singolo punto al primo livello. Mediante un processo iterativo, i dati iniziali vengono fusi in un cluster di dimensioni più grandi fino a che tutta la serie di dati non arriva a costituire un unico cluster (fig. 2a);
•  in un processo divisivo, invece, l’intera serie di dati rappresenta un unico cluster al primo livello. Questo viene poi suddiviso in sottogruppi fino a che ogni punto del grafico non arriva a rappresentare un singolo elemento (fig. 2b).

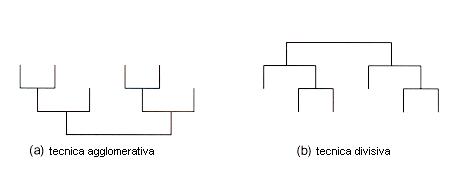
fig. 2

Aumentando il numero di punti il dendogramma diventa sempre più grande e meno leggibile e più difficoltoso risulta riconoscere su di esso le relative dimensioni di ogni gruppo.

Per risolvere questo problema si potrebbe visualizzare nel dendogramma un ulteriore caratteristica: il peso dei cluster. Esso è mostrato graficamente, per ciascun cluster, da un rettangolo di lunghezza proporzionale al peso stesso.

Questo nuovo diagramma prende il nome di pendrogramma. Su di esso si può facilmente calcolare il numero totale di cluster e il numero di livelli relativo (fig. 3).

fig. 3

Le tecniche di Cluster Analysis possono essere applicate in diversi ambiti della ricerca scientifica e, essendo applicabili sia su scala territoriale sia urbana, risultano efficaci nelle tematiche inerenti la zonizzazione per macro e micro modelli. Date delle zone con la propria destinazione d’uso, queste tecniche consentono di raggruppare le aree più simili in relazione ad uno specifico carattere (risorse, popolazione…), con lo scopo di ordinare il territorio in modo da avere un uso più razionale.

Gli obiettivi delle tecniche di classificazione sono:

• Ricerca di dati con un preciso criterio
• Riduzione di dati
• Adattamento di un modello (applicazione di una tecnica)
• Predizioni basate su determinati gruppi
• Formulazione di ipotesi
• Verifica di ipotesi

Per applicare la Cluster Analysis alla zonizzazione si fa riferimento a diversi parametri:

• parametri legati alla popolazione: densità, età istruzione, reddito, condizione sociale…;
• parametri legati al territorio: caratteristiche climatiche, topografiche, geologiche, morfologiche, idrologiche…;
• parametri urbanistici : dimensioni e quantità degli edifici, beni architettonici…;
• parametri relativi all’interazione tra popolazione e territorio: uso del suolo, andamento demografico, turismo,…;
• parametri relativi all’interazione tra popolazione e ambiente urbano: trasporti, comunicazioni, infrastrutture…;

 Expertise

 Quando si decide di utilizzare le tecniche di Cluster Analysis ci si trova a dover scegliere tra un notevole numero di metodi. Producendo ogni tecnica risultati diversi, e’ necessario esaminare i concetti fondamentali di ogni metodo e verificare quali soddisfano maggiormente le finalità da raggiungere e le caratteristiche del campione di dati in esame. Bisogna quindi fare una scelta sia per la tecnica sia per il criterio di raggruppamento degli elementi.

Si illustrano qui di seguito gli aspetti a cui occorre prestare particolare attenzione nell’effettuare l’applicazione di una qualsiasi tecnica di clustering:

1. definizione dei parametri caratterizzanti il campione di dati in esame. Ai parametri è strettamente collegata la definizione del problema che si intende risolvere, da questi stessi parametri dipenderà la successiva definizione del concetto di similarità. Individuare le caratteristiche degli oggetti risulta, quindi, fondamentale per dare una certa priorità nella classificazione. Se si mantiene lo stesso campione ma si modificano i parametri considerati, la classificazione potrà subire dei cambiamenti evidenziando differenti interazioni tra gli oggetti. Particolare attenzione va inoltre posta nell’identificare il minor numero di parametri indispensabili. La scelta di numero troppo elevato di caratteri causa l’aumento dei tempi di risoluzione del problema e non garantisce il raggiungimento dello scopo prepostoci.
2. valutazione della necessità di procedere alla normalizzazione (o standardizzazione) del campione di partenza. Si ricorda, infatti, che alcune tecniche di clustering (in particolar modo quelle che utilizzano una metrica di tipo Euclideo) producono risultati diversi in base alle caratteristiche dei dati di origine. L’operazione di standardizzazione può portare ad una sottostima delle differenze dei singoli gruppi, restringendo entro un più piccolo intervallo i valori che caratterizzano i parametri.
3. inserimento di eventuali vincoli. Solo operando attraverso l’introduzione di vincoli, che rappresentano connessioni reali tra i dati di partenza, il risultato della classificazione è dato da gruppi omogenei e compatti dal punto di vista dei parametri caratterizzanti il campione. I risultati in assenza di vincoli sono diversi da quelli ottenuti con la loro introduzione e rappresentano il risultato di un’analisi puramente statistica sui dati.
4. selezione del numero di gruppi su cui effettuare la classificazione. Questo aspetto riveste diversa importanza in relazione alla tecnica che utilizziamo. Per le tecniche di partizione, che si occupano dell’allocazione dei dati di partenza nei cluster ottimizzando determinati criteri, il numero iniziale di gruppi risulta molto importante. Per le tecniche gerarchiche, dove non si specifica qual è il numero ottimale di gruppi da utilizzare, questo aspetto può essere trascurato.
5. verifica di conformità dei raggruppamenti prodotti in relazione agli obiettivi che ci eravamo posti ed al metodo di risoluzione utilizzato. Come verifica si possono anche fare ipotesi sull’effetto che l’omissione di determinati parametri del campione produce sul raggruppamento e verificarle a posteriori.

In un procedimento di clustering esiste molta libertà di scelta per l’utente, sia per quanto concerne la modalità di classificazione che per il numero di parametri e di gruppi da considerare, è quindi opportuno, prima di mettersi al computer avere ben chiari lo scopo che ci si propone e le modalità operative con cui si intende perseguire il miglio risultato.

La Cluster Analysis è una tecnica molto utile ma richiede particolare attenzione nella sua applicazione, infatti, le procedure di classificazione, a differenza di altre tecniche statistiche, devono portare ad una corretta rielaborazione e valutazione dei risultati e non ad una semplice accettazione dei raggruppamenti ottenuti.

 Link e riferimenti

Per un approfondimento teorico relativo alla zonizzazione si può vedere :

Bartaletti F., “Principi e metodi per la delimitazione delle aree metropolitane “ , tratto da " Studi e ricerche di Geografia ", XV, 1994.

Bettini V.,“ L’analisi ambientale “ , Clup , Milano,1990.

Bresso M., Gamba G., Zeppetella A.,“ Valutazione ambientale e processi di decisione . Metodi e tecniche di valutazione di impatto ambientale “ , La Nuova Italia Scientifica , Roma, 1992.

Clemente F.,“ Pianificazione del territorio e sistema informativo “ , Franco Angeli , Milano, 1984.

Guarnero G.,“ Impatto ambientale . Informazione , analisi , valutazione , decisione “ , Alinea , Firenze, 1993.

Kmiec D.W.,“ Zoning and planning deskbook “ , West Group, 1986.

Maguire D. J., “ Il computer nello studio del territorio “ , Franco Angeli , Milano, 1990.

Marescotti L., Canevari A.,“ La cartografia per l’urbanistica e l’architettura “ , Clup , Milano, 1985.

Oneto G., “ Manuale di pianificazione del paesaggio “ , Pirola, 1997.

Scarci S.,” Informatica per l’ambiente . Strumenti per la ricerca , la sorveglianza , il supporto decisionale in campo ambientale “ , Franco Angeli , Milano, 1991.

Sorrentini F., “ Il parco Scientifico e Tecnologico come strumento di riqualificazione territoriale “ , in " Studi Geografici in onore di Domenico Ruocco ", II. Loffredo , Napoli, 1994.

Zonino V.,“ Una nota su cartografia e informatica “ , in " Studi Geografici in onore di Domenico Rocco ", II. Loffredo , Napoli, 1994.

Per un’analisi delle applicazioni relative alla Cluster Analysis i testi di base sono:

Coppi R., Bolasco S., “ Multiway Data Analysis “ , North Holland, 1988.

Diday E., “ New appracches in classification and data analysis “ , Springer, 1994.

Everitt B.,“ Cluster Analysis “ , Edward Arnold, 1993.

Goldstein H.,“ Multilevel statistical models “ , Arnold, 1995.

Gordon A., “ Classification “ , Chapman and Hall, 1981.

Hand D., Crower M., “ Pratical Longitudinal Data Analysis “ , Chapman and Hall, 1995.

Hazewinkel M.,“ Lipshits distance and hierarchical clustering “, 1995.

Jambu M., Lebeaux M.,“ Cluster analysis and data analysis “ , North Holland, 1983.

Rizzi A., “ Analisi dei dati “ , NIS, 1985.

Van Rijsberge C. J.,“ Automatic classification ” , 1995.

Watson S., “ The classification of metrics and multivariate statistical analysis “, 1996.