I numeri razionali
Consideriamo il prodotto cartesiano dell’insieme dei numeri razionali con se stesso: NxN=N2.
Il risultato sarà formato dalle infinite coppie di numeri naturali (a ; b).
Consideriamo la relazione di N2 in se stesso:

Tale relazione gode delle proprietà:
Riflessiva: (a;b)R(a;b)
poiché ba = ab
Simmetrica:
Se (a;b)R(c;d) à (c;d)R(a;b) poiché se ad=bc à cb=ad
Transitiva: Se(a;b)R(c;d) e (c;d)R(e;f ) à (a;b)R (e;f ) ; infatti: se ad=bc e cf=de àaf=be (con f¹0) (1)
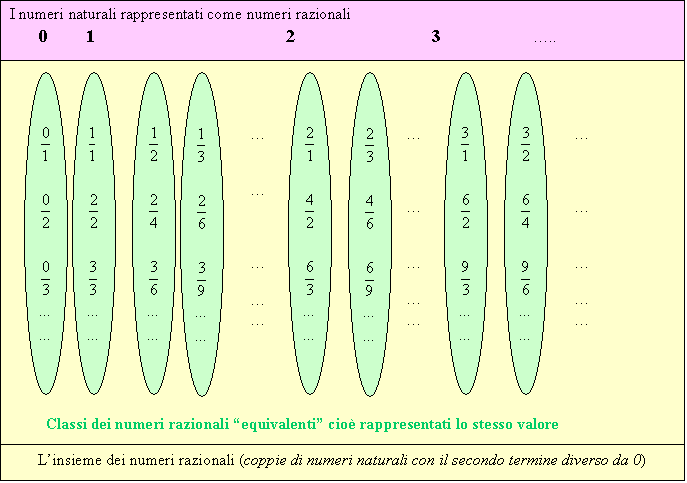
Pertanto la relazione è una relazione di equivalenza che permette di dividere l’insieme N2 in classi di equivalenza formate da tutte le coppie che sono in relazione fra loro.
Si può vedere che in ogni classe di equivalenza vi è solo una coppia in cui i numeri siano primi fra loro (2); tale coppia può essere considerata come elemento rappresentativo della classe di equivalenza.
Applicando le proprietà delle uguaglianze all’uguaglianza ad = bc si ha che:
![]()
Pertanto ogni classe di equivalenza può essere associata alle divisioni fra numeri interi che danno lo stesso risultato.
Notiamo che, nelle classi in cui gli elementi rappresentativi hanno il secondo numero uguale a 1, il risultato della divisione dei termini di ogni coppia (così come evidenziato in precedenza) corrisponde al numero naturale rappresentato dal primo termine della coppia rappresentativa della classe : ad esempio la coppia (3;1) corrisponde al numero naturale 3.
Le classi in cui gli elementi rappresentativi non hanno il secondo termine della coppia uguale a 1 possono essere, invece, associati alle divisioni fra numeri naturali in cui il risultato della divisione non può essere un numero naturale (ad esempio 3:2).
Si è ottenuto così un nuovo insieme di numeri che può rappresentare, oltre ai valori rappresentati dall’insieme dei numeri naturali, anche quantità che quest’ultimo non riesce a rappresentare.
Tale insieme prende il nome di INSIEME DEI NUMERI RAZIONALI.
Possiamo schematizzare il tutto nel modo seguente:
Nota (1): Applicando le proprietà delle uguaglianze numeriche e quelle della moltiplicazione e divisione fra numeri interi ( rappresentata per comodità di esposizione con il segno di frazione) si ha che:

Nota (2): Se (a ; b) e (c; d) sono coppie di numeri soddisfacenti la relazione e con i termini diversi, non nulli e primi fra loro, si ha che:

Poiché la prima possibilità non può essere presa in considerazione (per le ipotesi fatte né a/b, né d/c possono essere uguali a 1), resta solo la seconda possibilità: a/c=1 e d/b=1 à a=c e d=b
Se ( a ; b ) è una coppia di numeri diversi e primi fra loro, (c ; d ) non sono primi fra loro e le due coppie sono in relazione fra loro allora si ha che:
![]()
Perciò c e d sono rispettivamente multipli (con lo stesso fattore n) di a e di b.
Se (a;b) è una coppia di numeri uguali, allora anche (c;d), se è in relazione con (a;b), è una coppia di numeri uguali ed entrambe sono multipli della coppia formata da (1 ; 1 ).
Se (a;b) è una coppia con a = 0, allora anche (c;d), se è in relazione con (a;b), è una coppia con c = 0 ed entrambe sono multipli della coppia formata da (0 ; 1 ).
Possiamo concludere che tutte le coppie di una classe di equivalenza (per la relazione considerata) si possono ricavare moltiplicando, per uno stesso fattore, entrambi i termini di un’unica coppia di numeri primi fra loro.