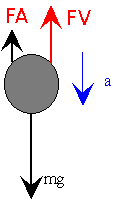
Moto di una sferetta immersa in un liquido
Le forze che agiscono in una sferetta che cade mentre è immersa in un liquido sono tre:
la forza peso
la spinta di Archimede
la forza di attrito con il mezzo in cui avviene il moto che dipende dalla velocità

La forza peso è costante e si può trovare moltiplicando la massa della sferetta per l'accelerazione di gravità che si può considerare uguale a 9,81 m/s2 . Dato che la densità è il rapporto fra massa e volume (ds=m/V, ds densità sferetta) si può trovare la massa moltiplicando la densità per il volume (m=ds·V). Tenendo conto della formula per il volume della sfera si ha:
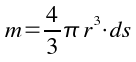
Moltiplicando questa massa per g accelerazione di gravità si ottiene la forza peso.
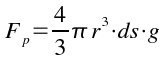
La spinta di Archimede è data dal peso del volume di fluido “spostato” dalla sferetta. In pratica il volume della sferetta deve essere moltiplicato per la densità d del liquido dove essa si muove e si ottiene la massa del liquido “spostato”. Per ricavare la forza peso della massa contenuta in questo volume di liquido ovvero la spinta di Archimede, occorre moltiplicare per g.
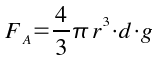
Per calcolare la forza di attrito del mezzo, detto attrito viscoso, che si oppone alla velocità si può fare ricorso alla legge di Stokes:
![]()
dove è la costante caratteristica del liquido che si chiama viscosità, r il raggio della sferetta e v la sua velocità.
Questa legge vale quando la velocità non è molto grande in modo tale che non si creino vortici o mulinelli nel liquido. In queste condizioni il moto avviene in regime laminare: relativamente alla sferetta il liquido si può immaginare come composto di tanti straterelli che scorrono l'uno sull'altro senza mescolarsi. Quando si creano vortici a velocità maggiori il regime viene detto turbolento.
Le dimensioni della viscosità [N·s/m2] si possono ricavare dalla legge di Stokes.
All'inizio del moto della sferetta, la forza peso prevale sulla somma della spinta di Archimede e della forza d'attrito e il moto avviene in modo accelerato. Aumentando però la velocità, aumenta anche la forza di attrito finché la risultante delle tre forze sarà nulla. Da quel momento in poi la sferetta raggiunge una velocità limite che non potrà aumentare dato che l'accelerazione è zero. In base al Principio d'Inerzia, se la risultante delle forze è nulla, il corpo mantiene costante la sua velocità.
Imponiamo la condizione:
![]()
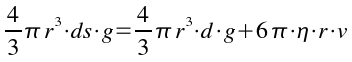
Semplificando r e isolando v si ha:
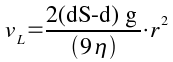
cioé la velocità limite è proporzionale al quadrato del raggio.
Volendo trovare la viscosità:
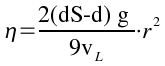
Se è valida la legge di Stokes, conoscendo la densità della sferetta dS, la densità del liquido dentro cui cade d ed il suo raggio r, basta misurare la velocità limite per trovare la viscosità. Questa velocità limite la si misura cronometrando il tempo entro il quale la sferetta percorre un intervallo di spazio assegnato.
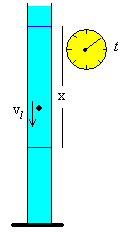
In un recente articolo intitolato “Correzioni alla legge di Stokes per la misura della viscosità di un liquido”, pubblicato dalla rivista dell'Associazione per l'Insegnamento della Fisica (AIF), La Fisica Nella Scuola XXXIX, 1, 2006, disponibile in Internet all'indirizzo:
autori V. L. Callegaro e P. Marazzini, si mette in evidenza che le dimensioni del recipiente contenente il liquido in cui cade la sferetta debbono essere molto grandi, teoricamente infinite, rispetto il suo raggio. La velocità di caduta inoltre deve essere bassa inferiore ad 1 cm/s per non creare vortici. I due autori inoltre riprendono vecchi studi per riproporre delle correzioni alla legge di Stokes per tener conto delle dimensioni finite del recipiente.
In base a tali lavori la velocità limite deve essere corretta moltiplicandola per due fattori:
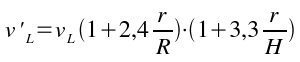
dove R indica il raggio del cilindro dentro cui cade la sferetta ed H l'altezza della colonna di liquido.
Malgrado questa correzione sulla velocità limite, il rapporto r/R dovrebbe essere inferiore a 0,1 e cioé il raggio del cilindro dieci volte più grande del raggio della sferetta.
Il calcolo ricorrente applicato alla caduta della sferetta
Scriviamo il Secondo Principio della dinamica applicato al moto di caduta della sferetta:
![]()
Sostituendo le espressioni precedentemente analizzate:
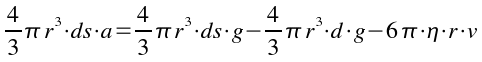
Semplificando e trovando a si ottiene:
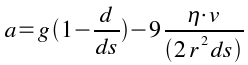
Questa formula è la base per realizzare un calcolo ricorrente con un elaboratore per poter trovare con ottima approssimazione come varia la velocità della sferetta al variare del tempo finché essa raggiunge la velocità limite.
A partire dai valori della posizione x e della velocità al tempo zero, si calcola l'accelerazione e dopo la nuova velocità dopo un piccolo intervallino di tempo dt e quindi la nuova posizione dopo un piccolo intervallino di tempo e così via ripercorrendo il ciclo di calcolo.
Di seguito la codifica in Python dell'algoritmo prima descritto (non dissimile da quella in altri linguaggi) che trova tante applicazioni in Fisica:
""" Simulazione caduta in un fluido di una sferetta che rispetta la legge di Stokes """
r=2E-3 #m r sferetta
d=1.28E3 #kg/m^3 densita'
dS=2.8E3 #kg/m^3 " sferetta
g=9.81 # m/s^2 acc. di grav.
eta=1.32 # N*s/m^2 viscosita' glicerina
def vai(x,v,tmax):
t=0
n=0
dt=0.0001
while t<=tmax:
a=g*(1-d/dS)-(9*eta*v)/(2*dS*r**2)
v=v+a*dt
x=x+v*dt
print t,' ',v
t=t+dt
n=n+1
vai(0,0,0.05)
Con sole quattro righe aggiunte è possibile realizzare il grafico della velocità al variare del tempo.
Esempio di misura con il
calibro. Ingrandimento della scala del nonio
(rossa) e di
quella dei millimetri (nera). La misura è 1,15 mm.

Indicazioni sperimentali
Misura della viscosità di un liquido tramite la legge di Stokes
E' necessario misurare il raggio della sferetta utilizzando un calibro.
Con una bilancia (di cui si annota la sensibilità) si può misurare la massa della sferetta. Da queste due misure si ricava la densità dS della sferetta come rapporto fra massa e volume.
Anche per il liquido dentro cui cade la sferetta è necessario misurare il volume e la massa per calcolarne la densità d.
Note le due densità, si passa alla misura con un cronometro del tempo di caduta della sferetta per uno spazio predeterminato. In altre parole si ricava la velocità limite costante perché in assenza di forze.
Sostituendo i valori si ottiene in fine la viscosità:
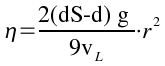
E' possibile introdurre delle correzioni alla velocità limite:
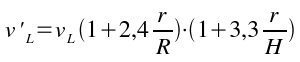
dove R indica il raggio del cilindro dentro cui cade la sferetta di raggio r ed H l'altezza della colonna di liquido; e ricalcolare la viscosità in modo più accurato.